R^2 점수란?
R^2 (결정계수)은 회귀 모델의 성능을 평가하는 지표로, 1에 가까울수록 더 좋은 성능을 의미
count 값을 예측하는 모델
최대한 r^2 값을 높게 만들어보기




부스팅의 기본 개념
부스팅(Boosting)은 약한 학습기(Weak Learners)를 연속적으로 학습시켜 점차적으로 모델의 성능을 개선하는 방법
각 단계에서 학습기는 이전 학습기들이 잘못 예측한 데이터에 대해 더 집중하여 학습한다.
- 첫 번째 모델: 데이터를 학습하여 예측을 만듭니다. 틀린 데이터에 가중치를 더 부여한다.
- 두 번째 모델: 첫 번째 모델이 틀린 데이터를 집중적으로 학습한다. 또다시 틀린 데이터에 가중치를 부여한다.
- 세 번째 모델: 두 번째 모델이 틀린 데이터를 학습한다.
- 최종 예측: 모든 모델의 예측을 결합하여 최종 예측을 만든다.
부스팅에서는 각 학습기의 예측 결과를 더해 나가는 방식으로 최종 예측을 한다.
예를 들어, 첫 번째 모델의 결과에 두 번째 모델의 결과를 가중합하여 최종 예측을 점진적으로 개선함.
XGBoost의 원리
XGBoost는 부스팅 알고리즘의 하나로, 특히 Gradient Boosting의 원리를 기반으로 한다.
여기서 중요한 차이점은:
- 잔여 오차(Residual Error)를 줄이는 방향으로 새로운 모델을 학습한다. 각 새로운 모델은 이전 모델들의 오차를 줄이기 위해 학습됨.
- 가중치 부여: 각 데이터 포인트는 이전 모델이 틀린 데이터 포인트에 대해 더 높은 가중치를 부여하며, 이 가중치에 따라 새로운 모델이 학습됨.
구체적인 예:
- 첫 번째 모델이 예측을 했을 때, 예를 들어 700개를 맞추고 300개를 틀렸다면, 이 300개의 오차가 생성된다.
- 두 번째 모델은 이 오차(즉, 300개의 데이터)에 대해 학습하여 이 오차를 줄이는 방향으로 예측을 한다. 이 과정에서 200개를 맞추고 100개의 새로운 오차가 발생할 수 있다.
- 세 번째 모델은 이 100개의 오차를 학습하여 예측을 하며, 그 중 50개를 맞추고 50개의 오차가 남을 수 있다.
- 최종 모델: 모든 모델의 예측을 가중합하여 최종 예측을 하게 된다. 최종적으로 1000개의 데이터 중 950개를 맞추고 50개의 오차가 남을 수 있다.
# XGBoost 학습 원리
# 부스팅 : 약한 학습기 (찍는것 보단 나은 수준)
약한 학습기는 성능이 안좋은 트리 모델
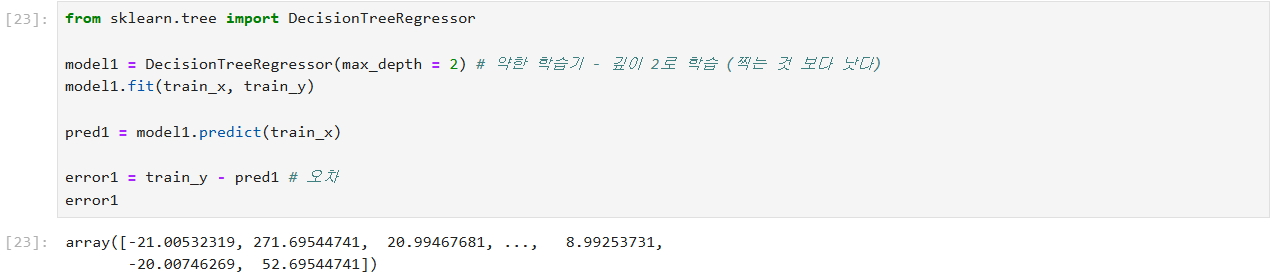

부스팅(Boosting) 원리
첫번째 모델이 700 맞고 300 틀리면
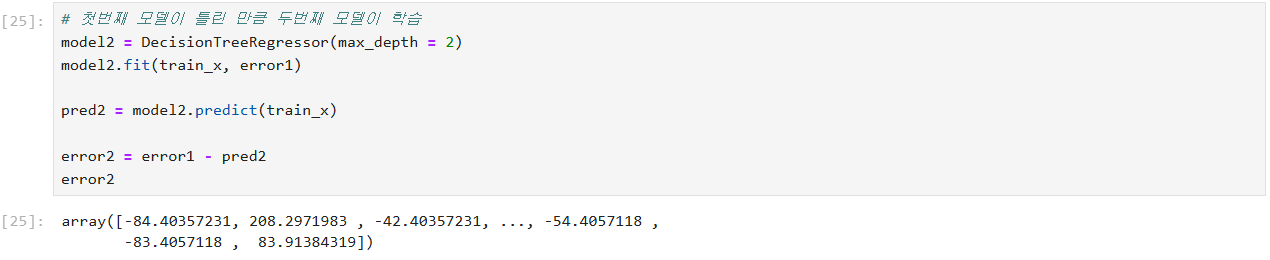
두번째 모델이 300에 대해서 예측함
두번째 모델이 200 맞고 100 틀리면
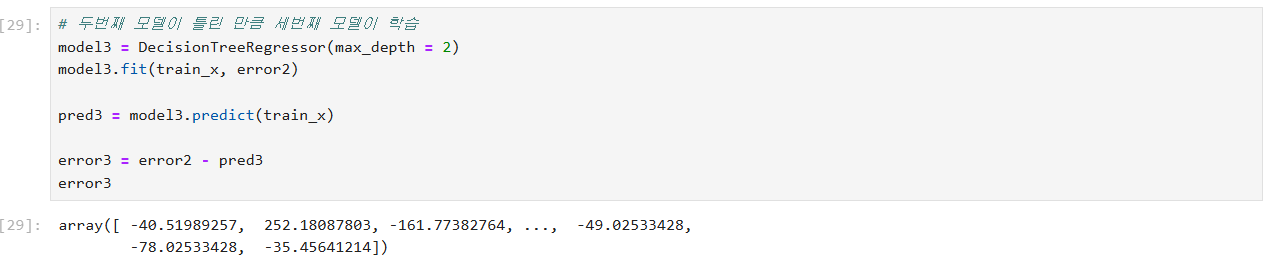
세번째 모델이 100에 대해서 예측함
세번째 모델이 50 맞고 50 틀리는 경우
1000에 대해서 50이 오차

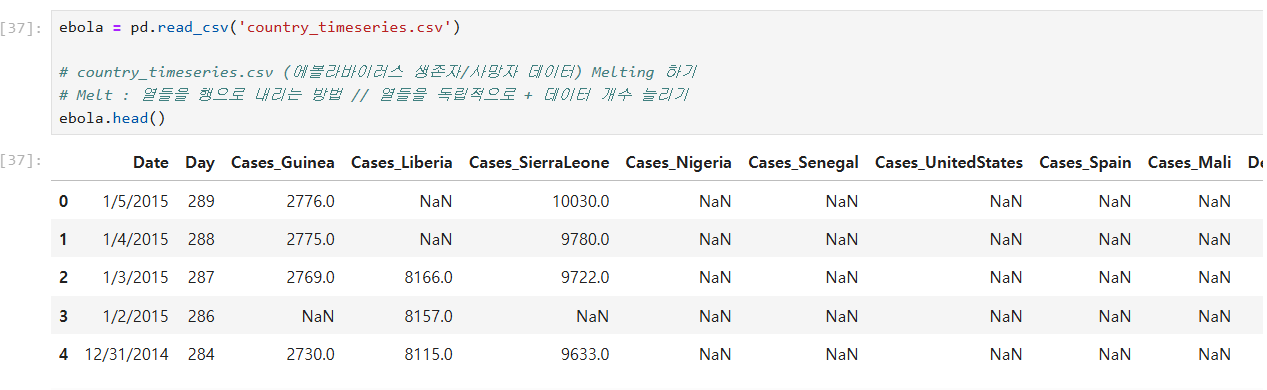
# country_timeseries.csv (에볼라바이러스 생존자/사망자 데이터) Melting 하기
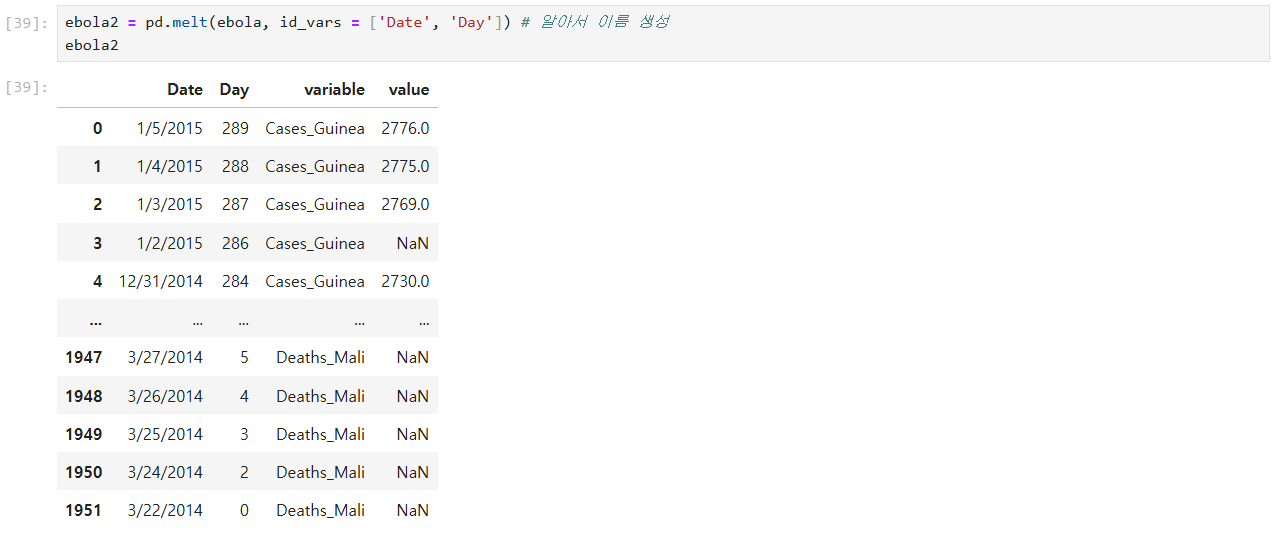
# Melt : 열들을 행으로 내리는 방법 // 열들을 독립적으로 + 데이터 개수 늘리기
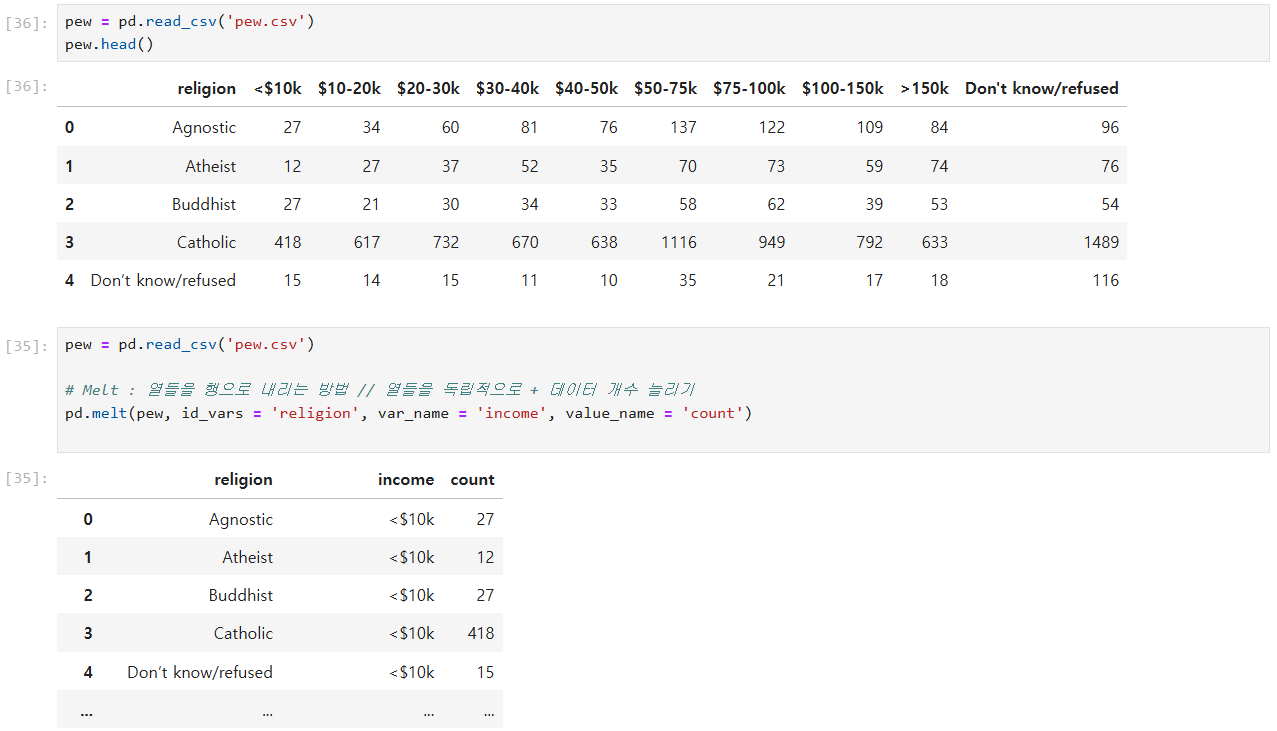
country_timeseries.csv (에볼라바이러스 생존자/사망자 데이터) Melting 하기
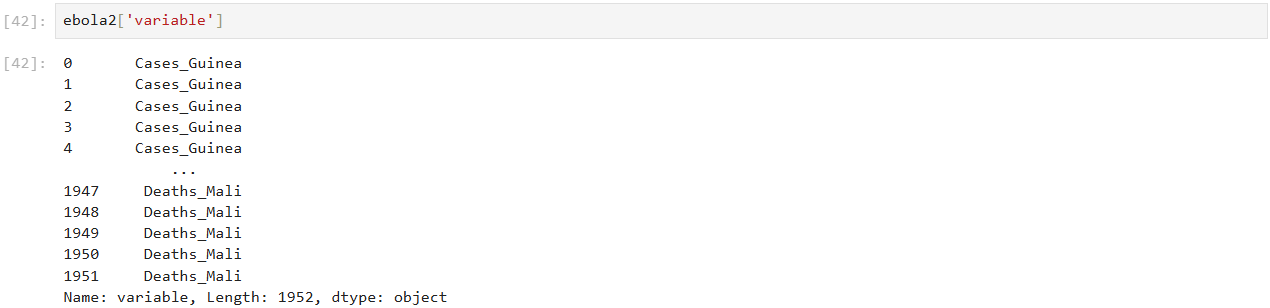
시리즈 안의 값 접근하니 문자열 -> 문자열 함수 사용 가능
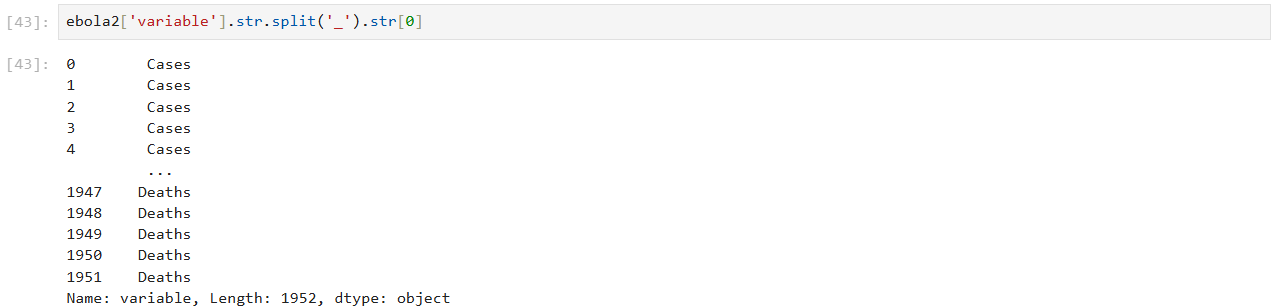
시리즈 안으로 접근 가능.
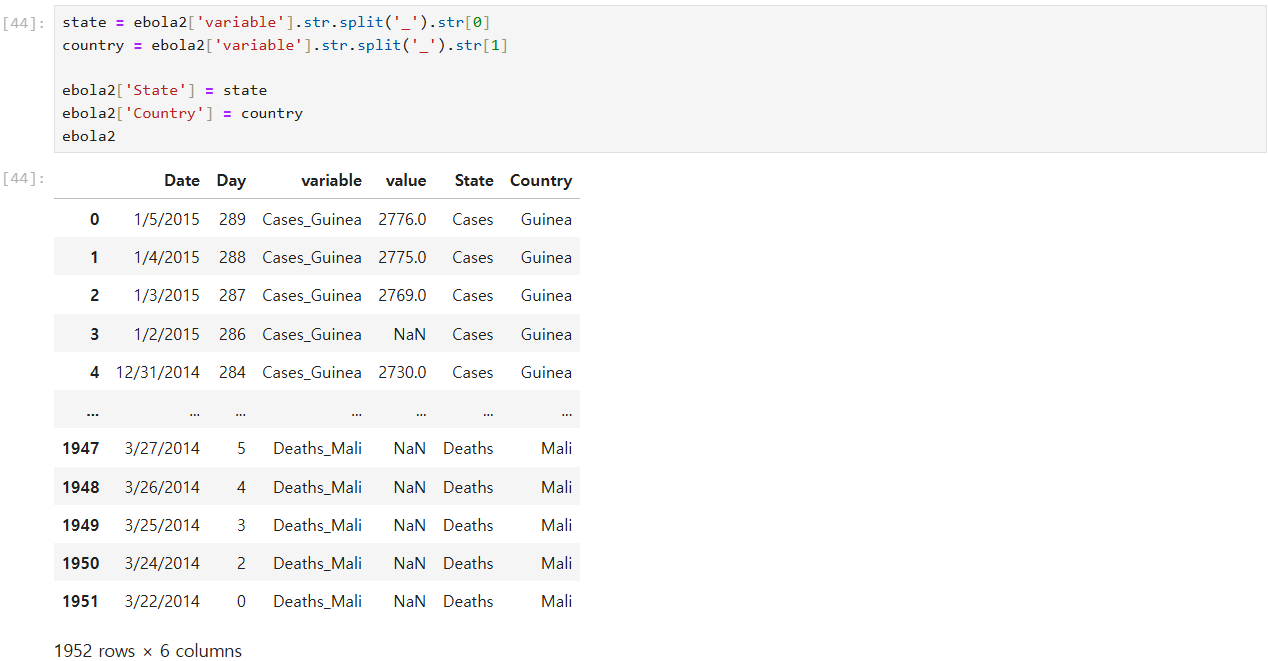
누락값 처리 해보기
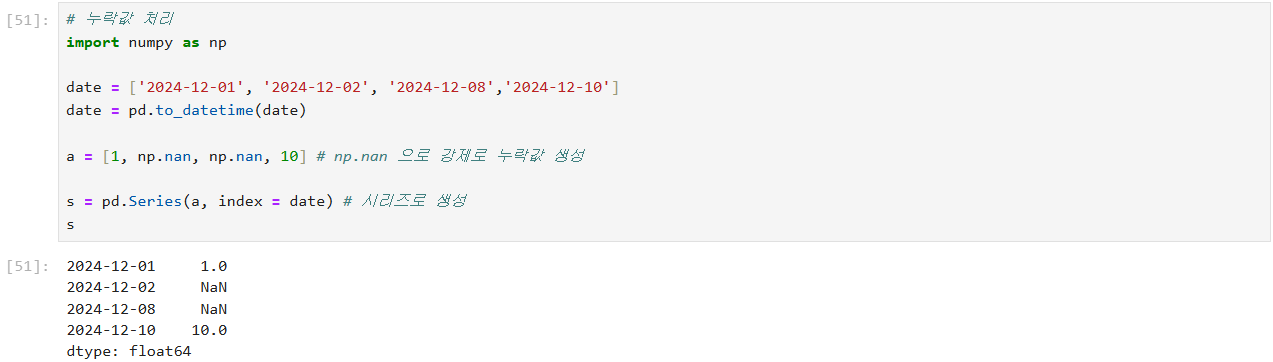


위 ebola 의 누락값도 채워보기
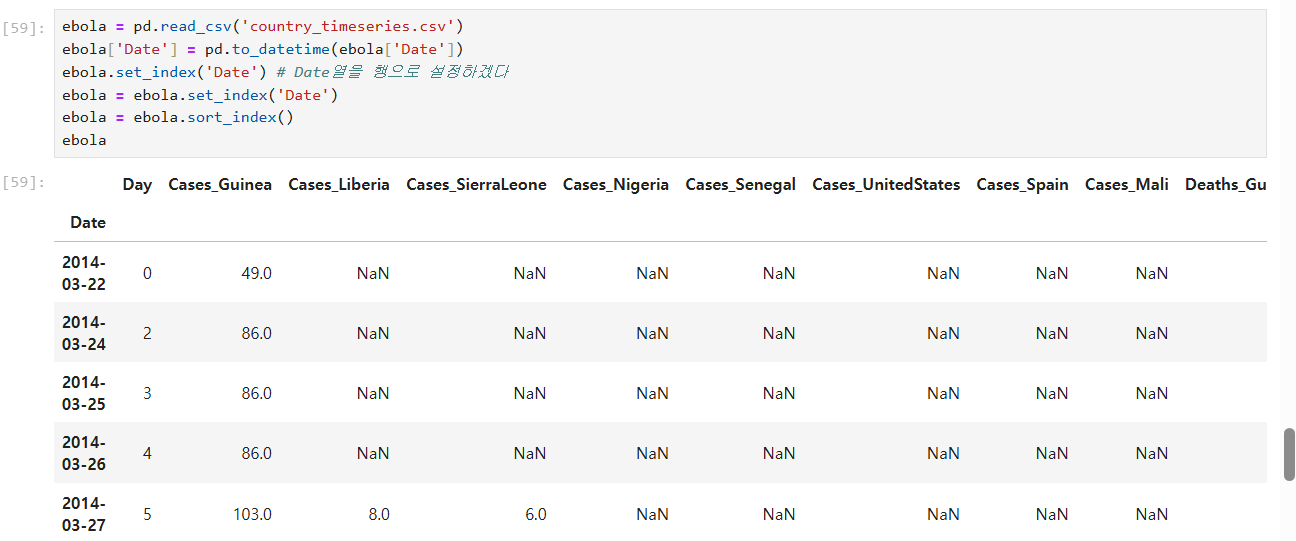
앞뒤로는 시간의 흐름을 알 수가 없음
-> ffill (앞의 값으로 가져오겠다.)
-> bfill (뒤의 값으로 가져오겠다.)
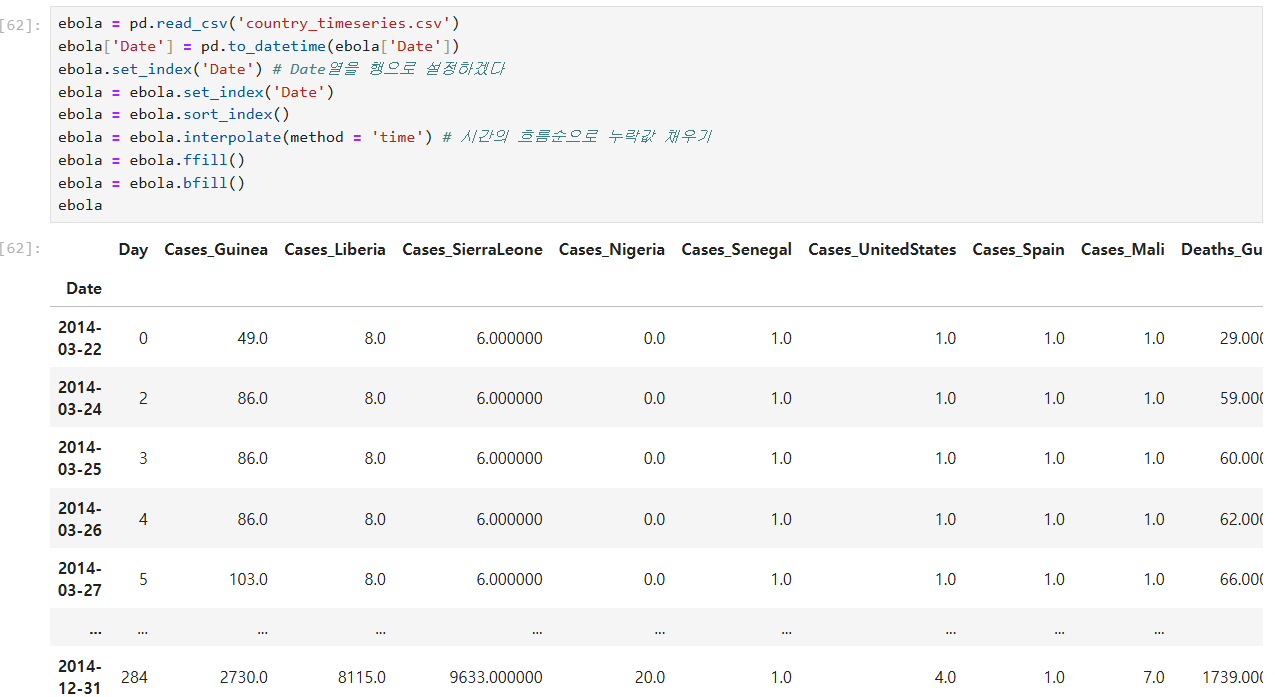
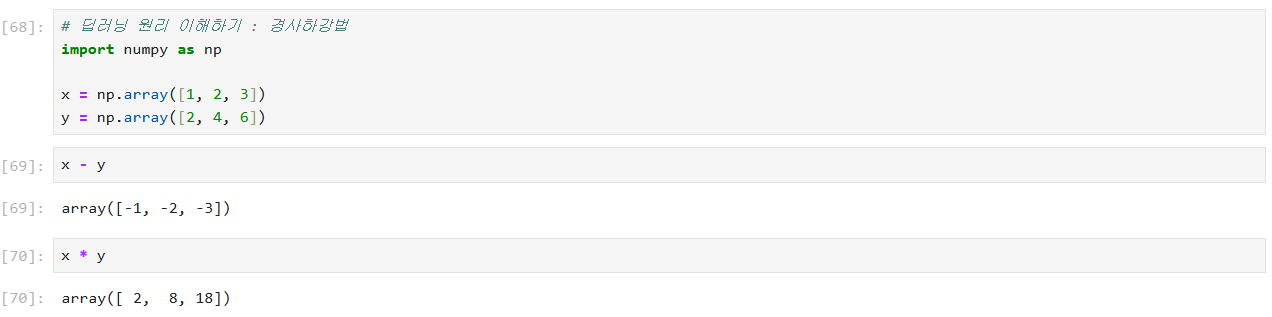
딥러닝 원리 이해하기 : 경사하강법
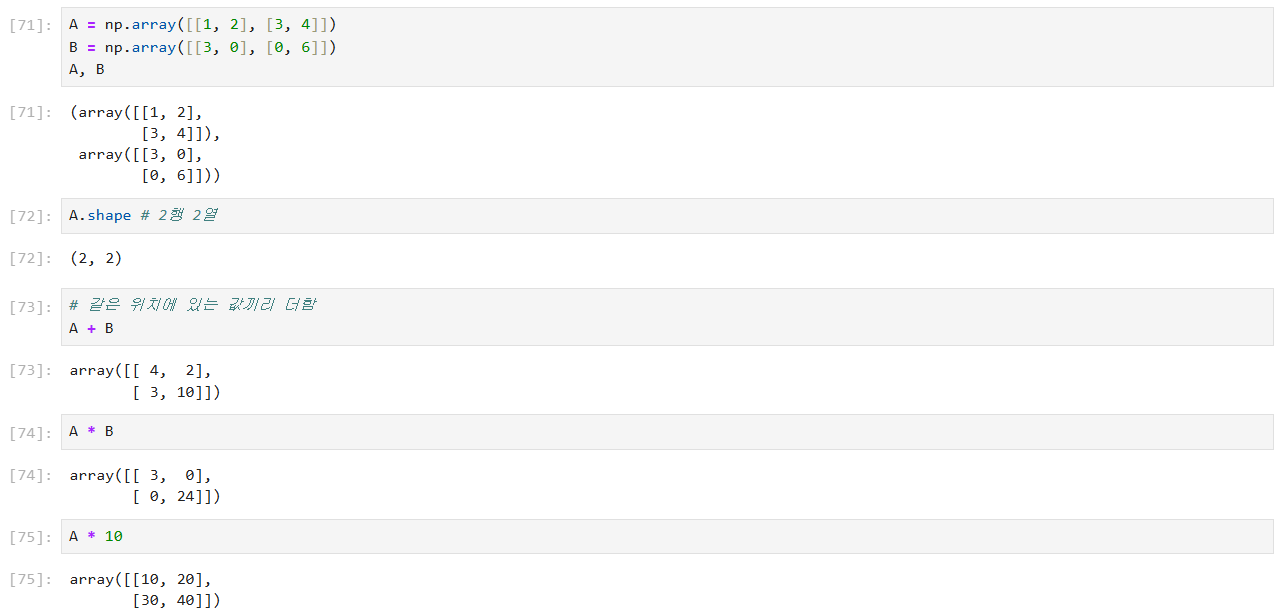

OR와 AND의 퍼셉트론 모델
퍼셉트론에서 출력값은 다음과 같이 계산
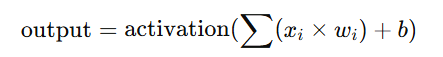
여기서 xix_i는 입력값, wi는 가중치, b는 편향
활성화 함수는 주로 계단 함수(step function)로, 결과가 0보다 크면 1을, 그렇지 않으면 0을 출력
AND함수
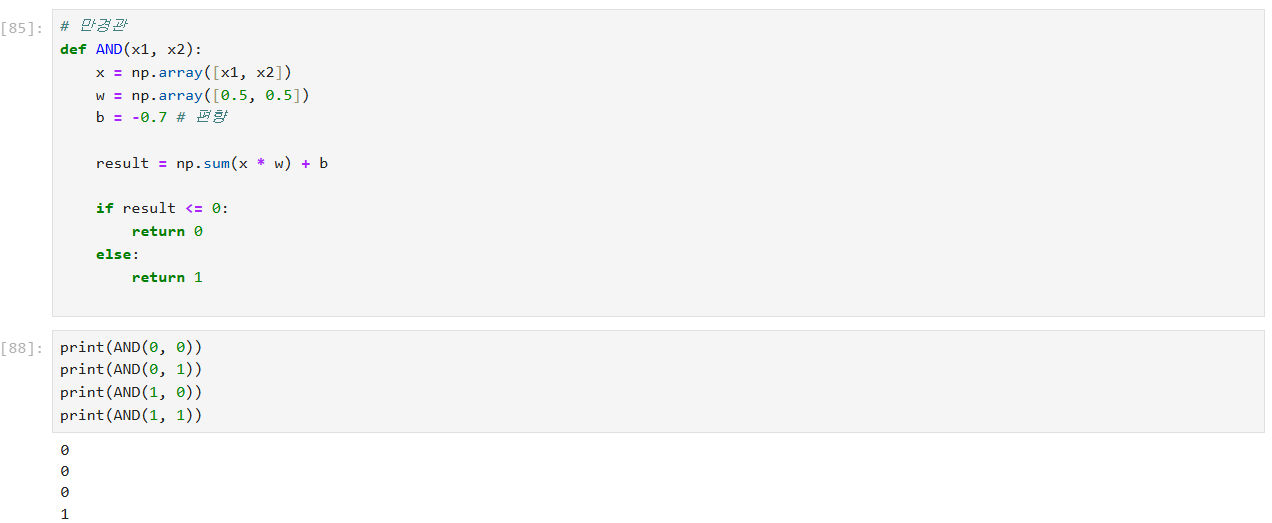
OR 함수
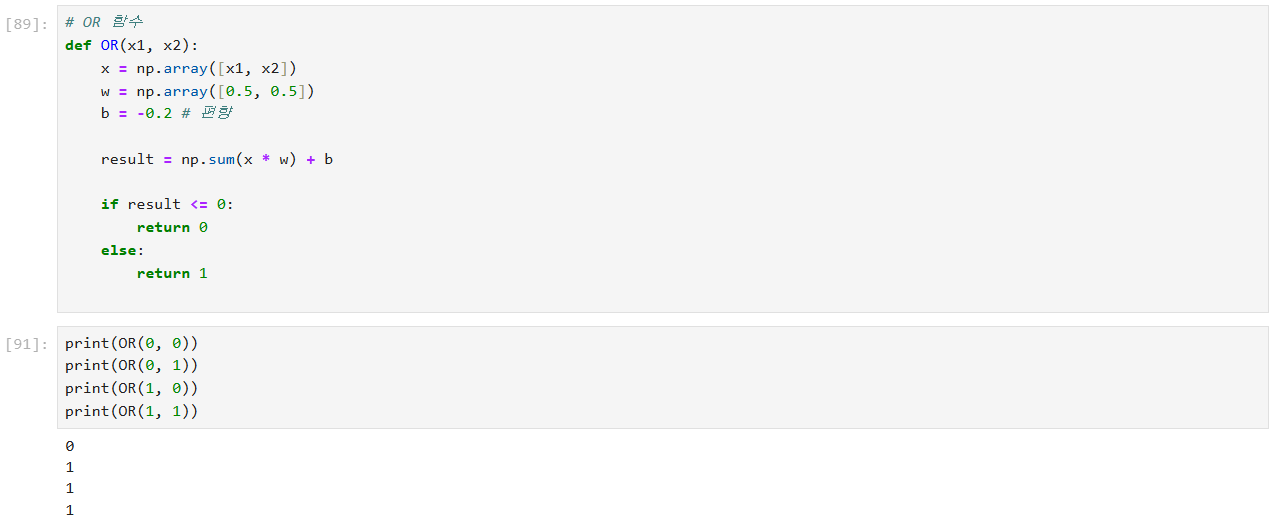
NAND 함수
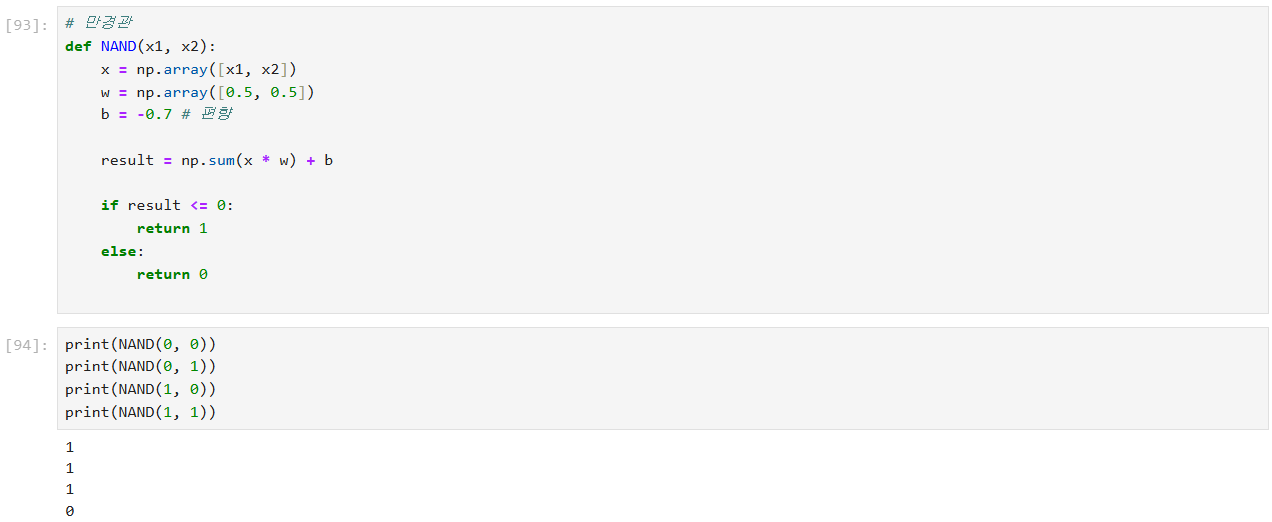
XOR 함수
배타적 논리합(XOR, Exclusive OR)을 구현하기 위해 퍼셉트론을 사용
NAND와 OR 연산을 통해 중간 결과를 만든 다음,
이 중간 결과들을 AND 연산을 통해 결합하여 최종 XOR 출력을 생성
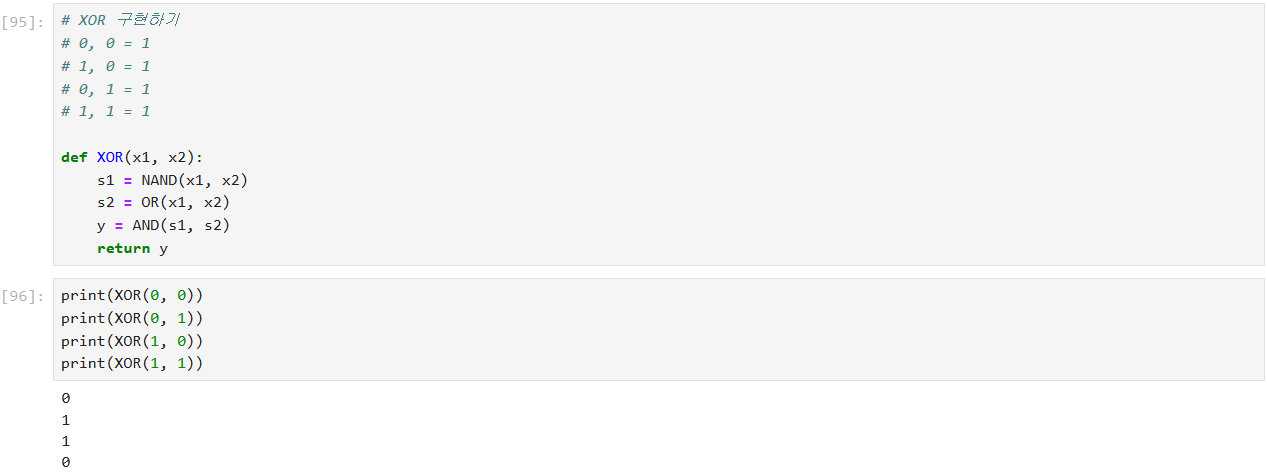
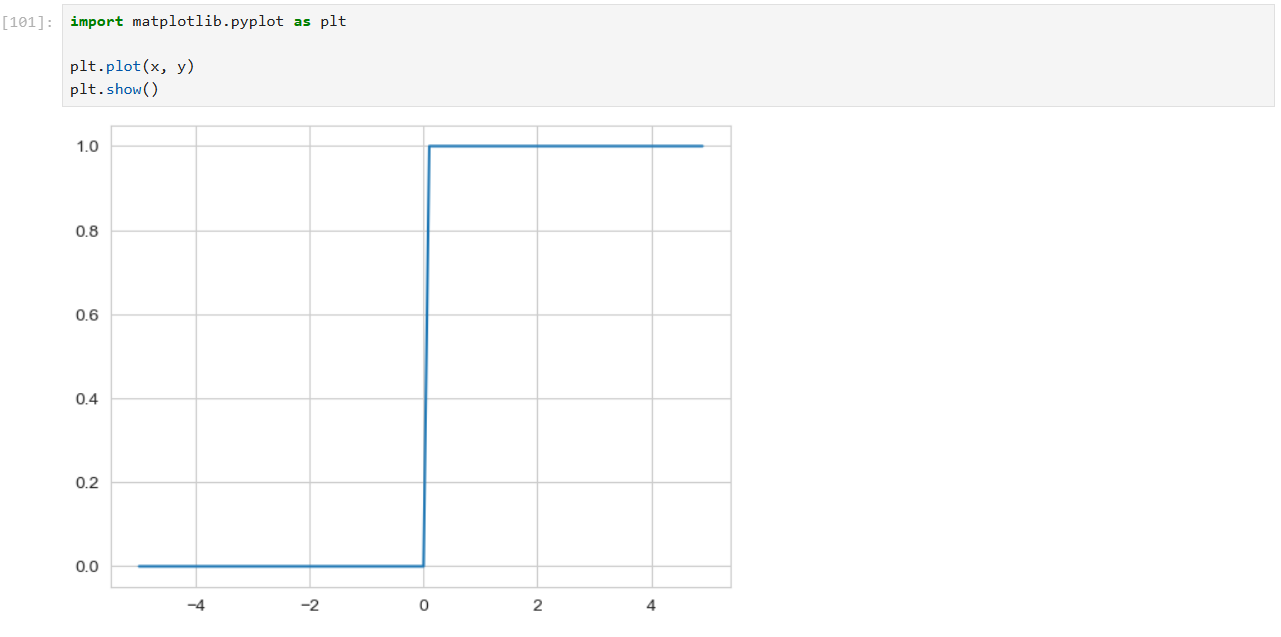
단위 계단 함수
종종 인공 신경망에서 활성화 함수로 사용되며, 입력의 부호에 따라 이진 출력을 만들어내는 역할
입력값이 0보다 크면 1을, 그렇지 않으면 0을 반환하는 단순한 함수로, 입력값의 부호를 기준으로 출력을 결정
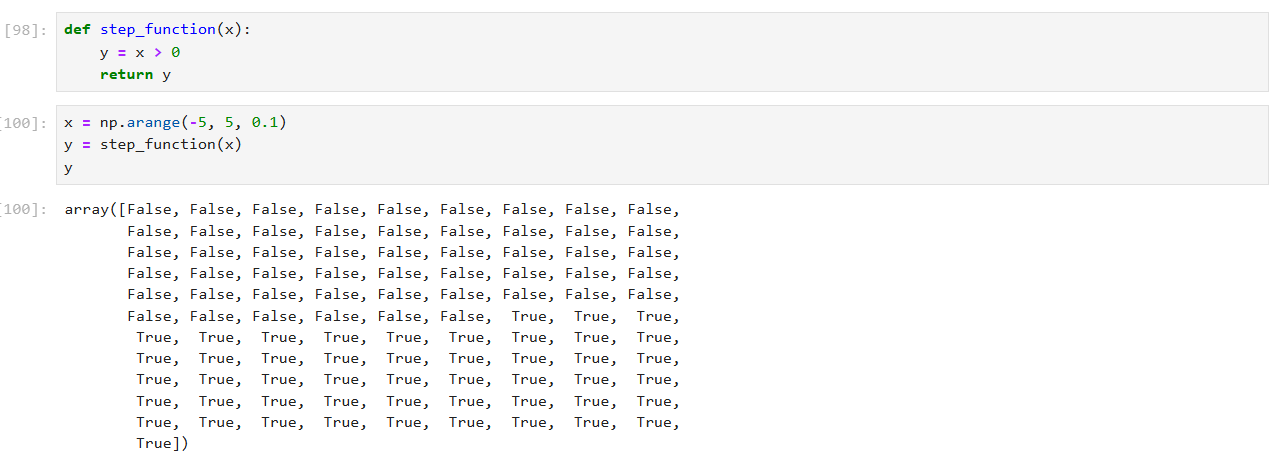
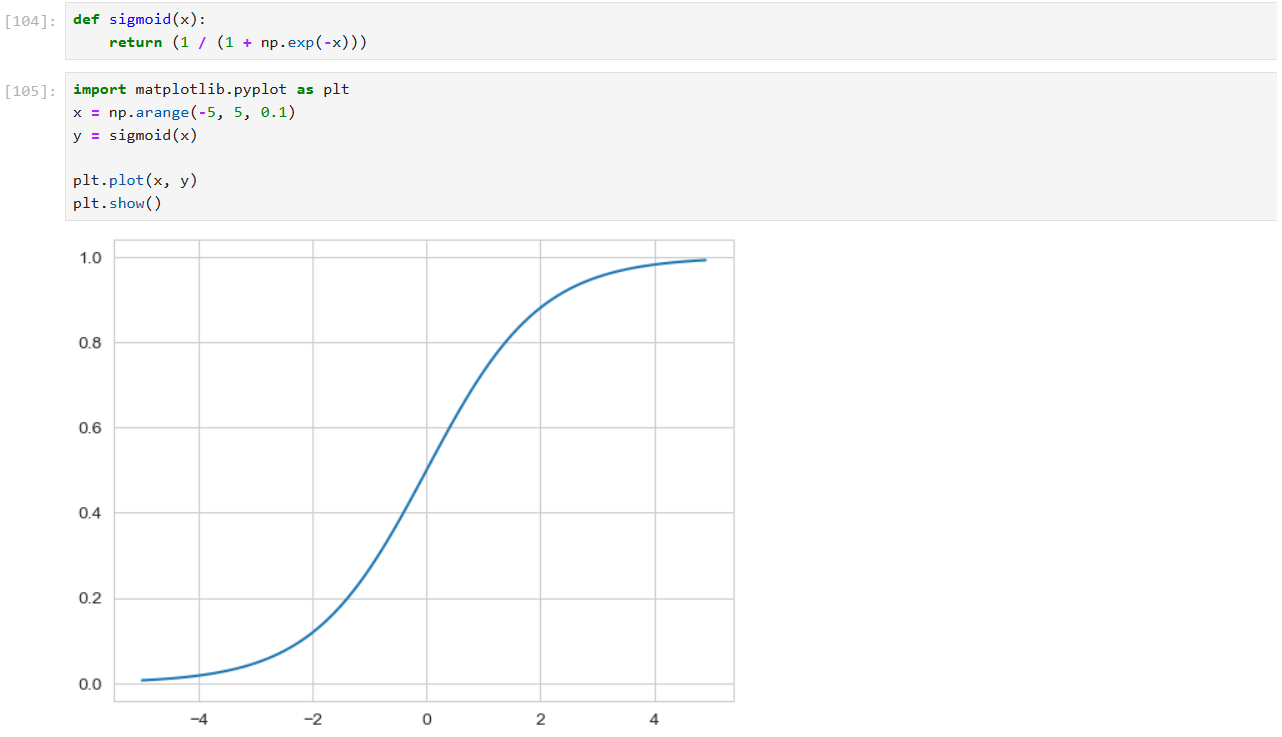
시그모이드 함수
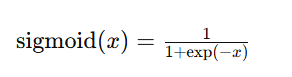
시그모이드 함수의 특징
- 출력 범위: 시그모이드 함수의 출력은 항상 0과 1 사이
- 모양: 시그모이드 함수는 S자 형태의 곡선을 가지며, 입력값이 0일 때 출력값이 0.5이다. -> 입력값이 크게 양수일 때는 출력이 1에 가까워지고, 입력값이 크게 음수일 때는 출력이 0에 가까워진다.
행렬 곱셈을 통해 선형 변환(linear transformation)

선형 변환과 시그모이드 활성화 함수를 적용하여 신경망 뉴런의 출력을 계산

신경망의 한 뉴런에서 입력 벡터와 가중치, 편향을 통해 선형 결합을 계산하고,
이 결과에 시그모이드 함수를 적용하여 비선형 변환을 수행하는 전형적인 뉴럴 네트워크 연산

신경망의 두 번째 층에서의 출력을 계산
여기서는 선형 변환을 수행한 후, 시그모이드 활성화 함수를 적용하여 최종 출력

신경망의 세 번째 층에서의 선형 변환을 계산
앞서 계산된 Z2 벡터와 새로운 가중치 W3, 편향 b3를 사용하여 최종 출력을 얻음
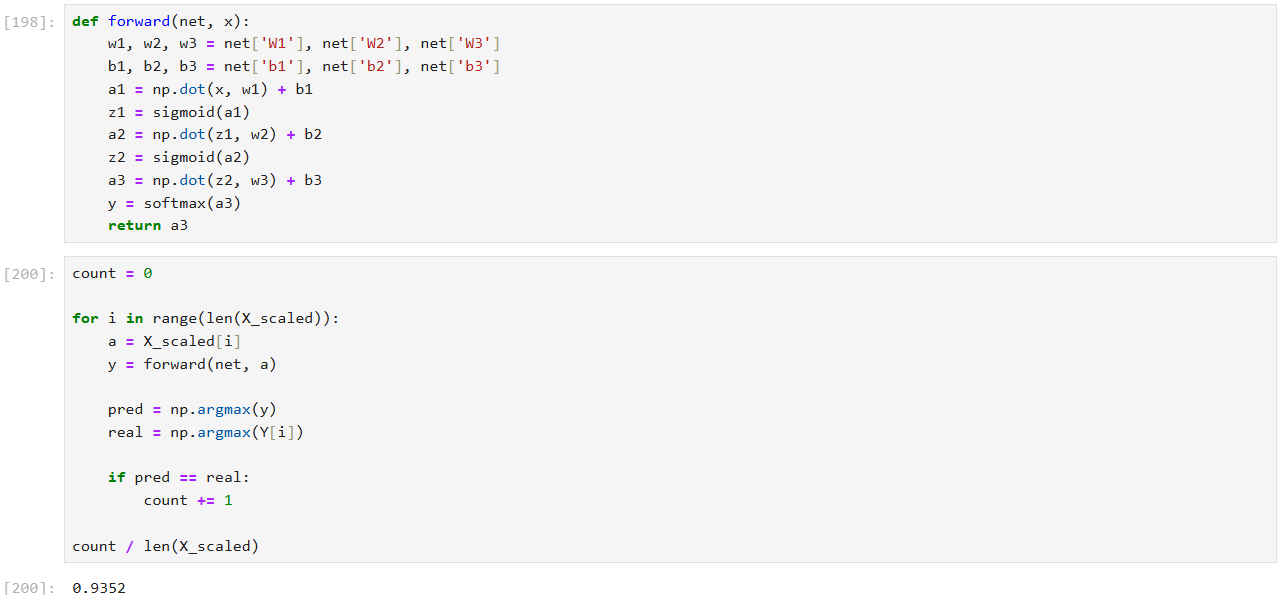
다층 신경망(multi-layer neural network)의 순전파(forward propagation) 과정을 구현
순전파 과정은 입력 데이터가 네트워크를 통과하면서
각 층에서의 선형 변환과 비선형 변환을 통해 최종 출력을 계산하는 과정

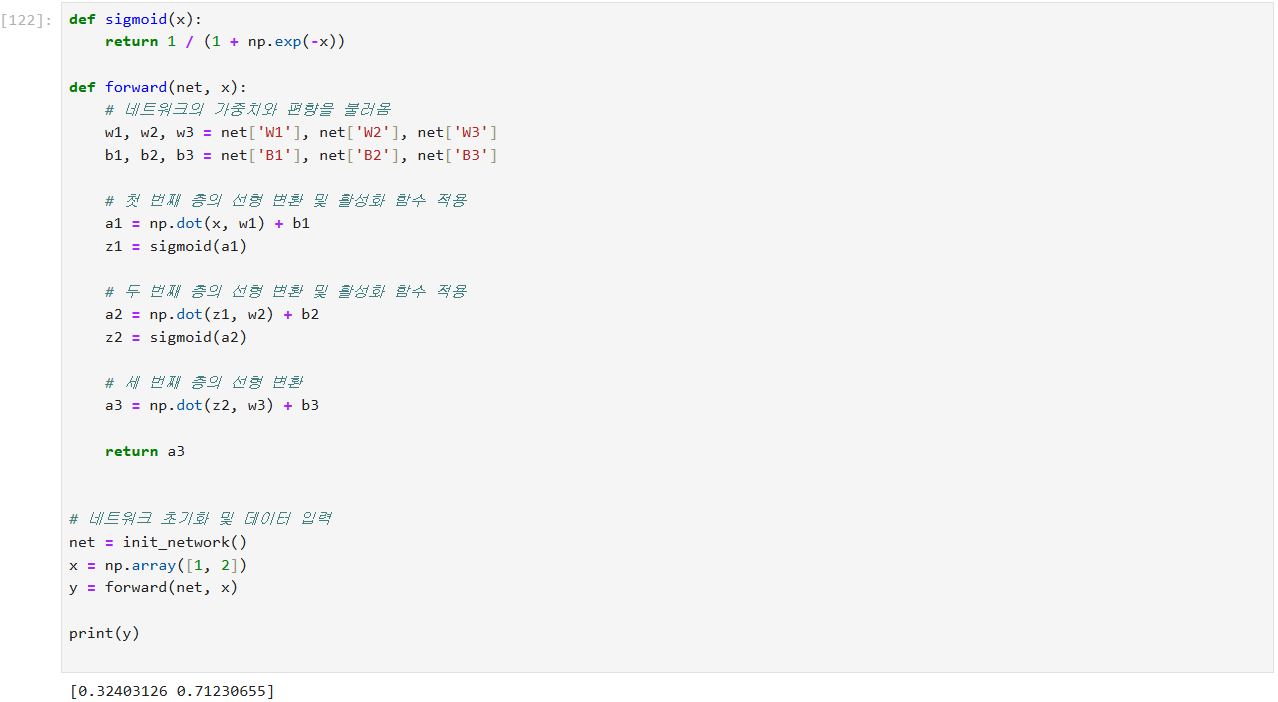
-> 입력 데이터 x를 네트워크를 통해 전달하여 최종 출력을 계산
이 과정에서 각 층의 선형 변환과 활성화 함수를 적용함.
소프트맥스 함수
다중 클래스 분류 문제에서 모델의 출력을 확률로 변환하는 데 사용
입력 벡터의 각 요소를 확률로 변환하여, 각 요소가 특정 클래스에 속할 확률을 나타내도록 함.
이 확률의 합은 항상 1이 된다.
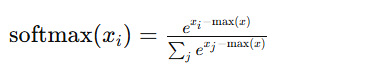
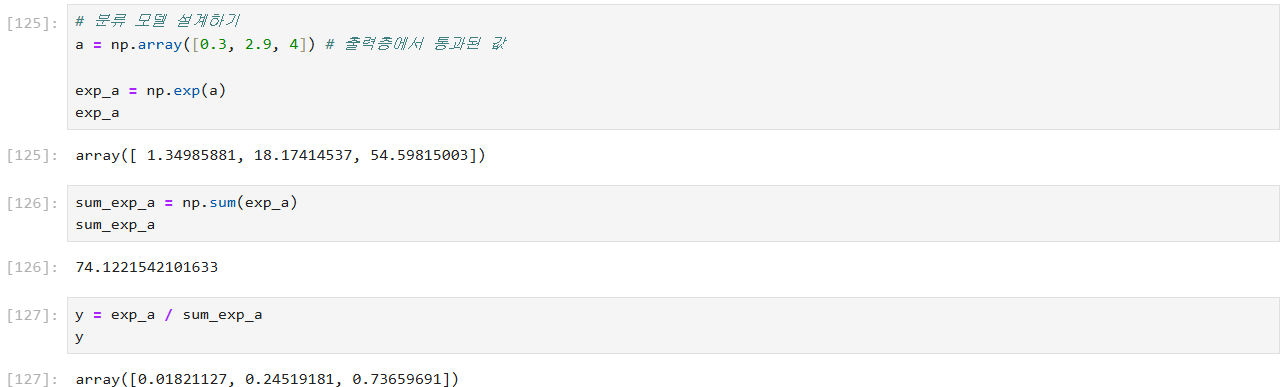

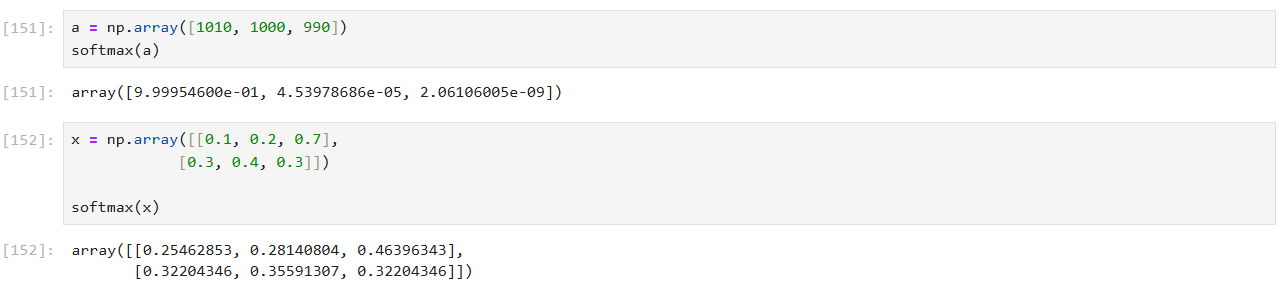
- 1차원 배열의 소프트맥스 계산:
- 입력: x는 1차원 배열 (벡터)
- 최대값 계산: np.max(x)를 사용하여 입력 벡터 x에서 최대값 c를 구한다.
- 지수 함수 적용: x - c를 사용하여 지수 함수를 적용합니다. 최대값을 빼는 이유는 오버플로우를 방지하기 위함임
- 정규화: 지수 함수의 결과 exp_a의 총합 sum_exp_a로 나누어 확률을 계산. 이 결과 y는 확률 벡터임.
- 2차원 배열의 소프트맥스 계산:
- 입력: x는 2차원 배열 (행렬)입니다. 각 행은 서로 다른 데이터 샘플을 나타낸다.
- 행별 최대값 계산: np.max(x, axis=1).reshape(-1, 1)을 사용하여 각 행의 최대값을 계산하고 이를 열 방향으로 확장하여 c를 만든다.
- 지수 함수 적용: x - c를 사용하여 지수 함수를 적용. 각 행의 최대값을 빼서 오버플로우를 방지
- 행별 총합 계산: np.sum(exp_a, axis=1).reshape(-1, 1)을 사용하여 각 행의 지수 함수 결과의 총합을 계산하고 이를 열 방향으로 확장하여 sum_exp_a를 만든다.
- 정규화: 지수 함수 결과 exp_a를 각 행의 총합 sum_exp_a로 나누어 확률을 계산. 이 결과 y는 각 행별 확률 분포를 포함하는 행렬
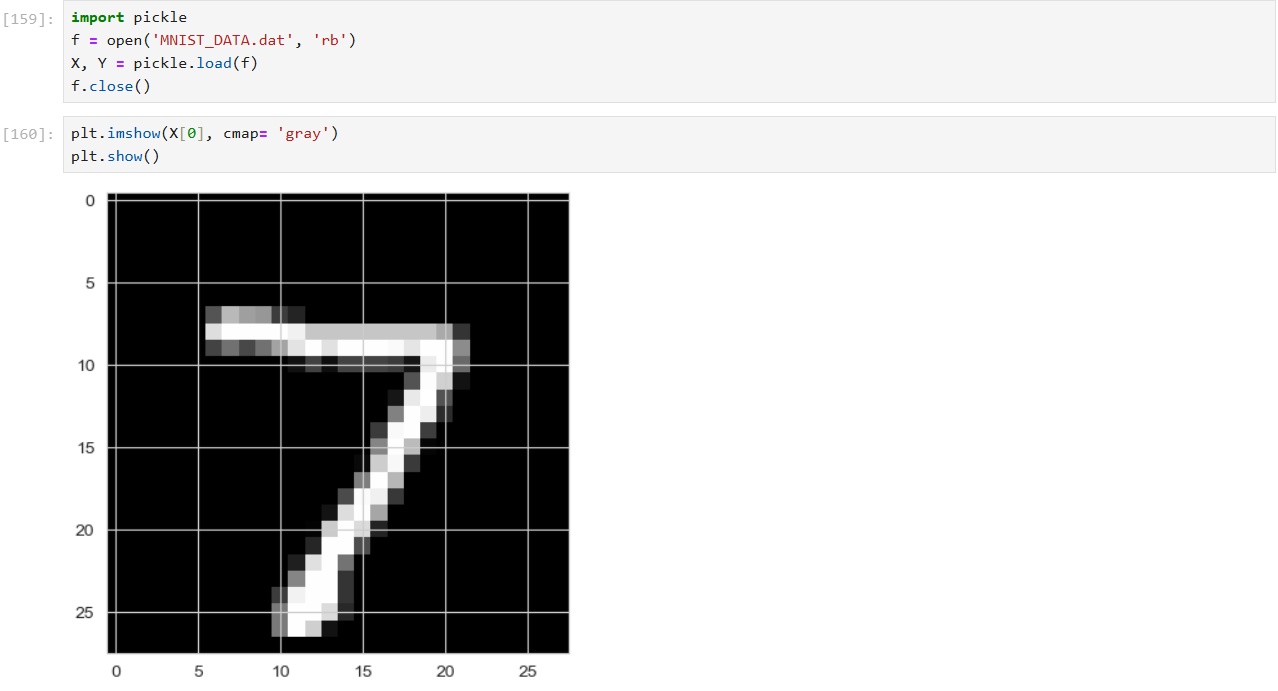
크로스 엔트로피 손실의 개념
크로스 엔트로피 손실은 분류 문제에서 모델이 얼마나 정확하게 예측했는지를 측정하는 지표
예측된 확률이 실제 값과 얼마나 가까운지를 평가함



- y가 1차원 배열이므로, y와 t가 2차원으로 변환된다.
- 그런 다음, y[np.arange(size), t]에서 size = 1이 되고, y[0, 1] = 0.8이 선택된다.
- 이 값을 가지고 -np.log(0.8 + 1e-9)가 계산됩니다. 이는 로그 손실 값을 계산하여 반환한다.
- cross_entropy_error 함수는 모델의 예측 확률과 실제 레이블 간의 크로스 엔트로피 손실을 계산.
- y가 1차원 배열일 경우 이를 2차원 배열로 변환하여 일관성을 유지하며, t가 클래스 인덱스로 주어졌을 때 이를 사용해 손실을 계산함.
미분 함수 구현하기

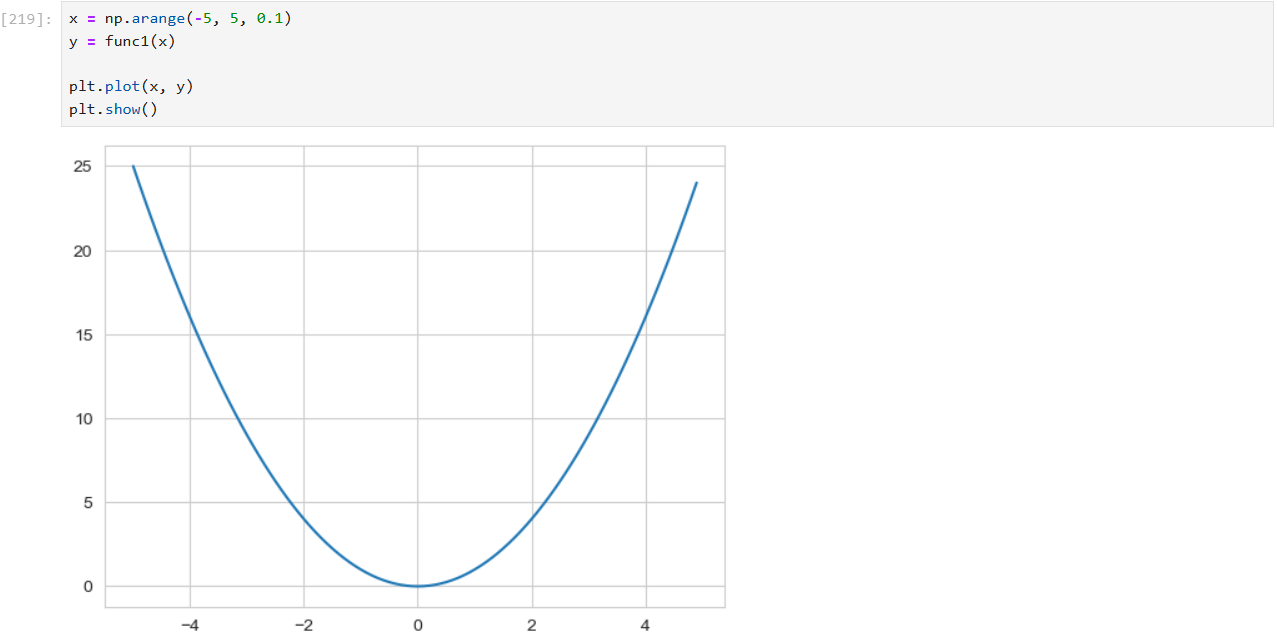

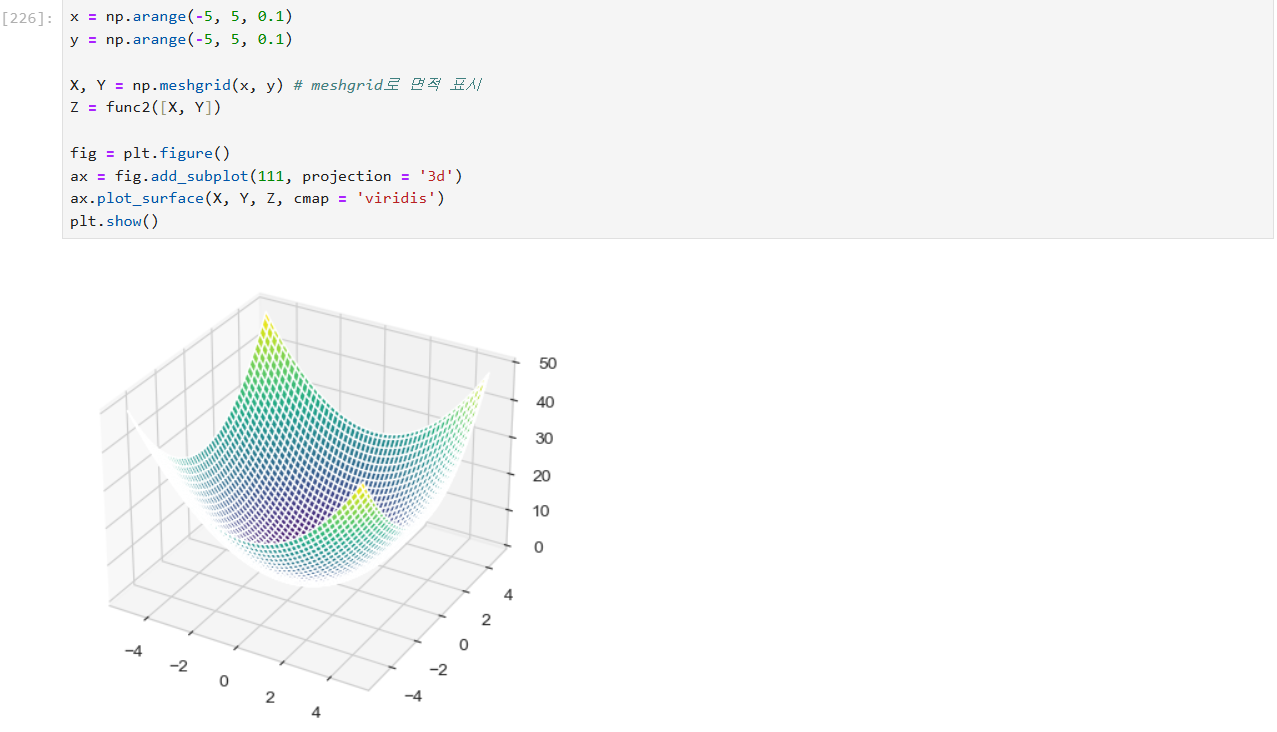
수치 미분(gradient) 계산
수치 미분은 함수의 기울기를 근사적으로 계산하는 방법
각 변수에 대해 조금씩 값을 변화시켜 함수의 변화율을 계산
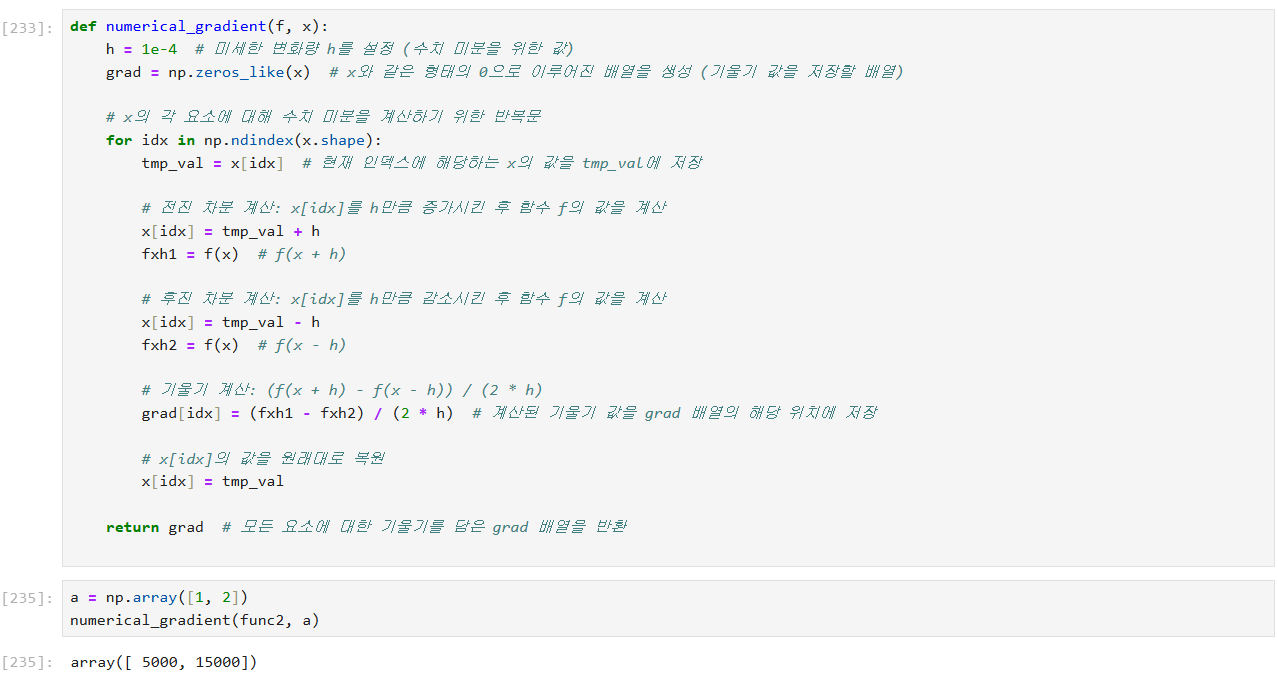
- 를 계산하기 위해 현재 변수의 값을 h만큼 증가시키고, 그 결과를 fxh1에 저장.
- f(x−h)를 계산하기 위해 현재 변수의 값을 h만큼 감소시키고, 그 결과를 fxh2에 저장.
- 편미분은 (fxh1 - fxh2) / (2 * h)로 계산되며, 이는 해당 변수의 기울기다.
- 계산 후에는 변수의 값을 원래 상태로 복원함.
신경망 모델의 구현을 위한 클래스
class My_Net:
def __init__(self, input_size, hidden_size, output_size):
# 입력층, 은닉층, 출력층의 뉴런 수를 설정
I, H, O = input_size, hidden_size, output_size
# 네트워크의 파라미터(가중치와 편향)를 초기화
self.params = {}
self.params['w1'] = np.random.rand(I, H) # 입력층에서 은닉층으로 가는 가중치
self.params['b1'] = np.random.rand(H) # 은닉층의 편향
self.params['w2'] = np.random.rand(H, O) # 은닉층에서 출력층으로 가는 가중치
self.params['b2'] = np.random.rand(O) # 출력층의 편향
def predict(self, x):
# 입력 데이터 x를 받아서 예측값을 반환하는 메소드
w1, w2 = self.params['w1'], self.params['w2']
b1, b2 = self.params['b1'], self.params['b2']
# 입력층에서 은닉층으로의 선형 변환
a1 = np.dot(x, w1) + b1
# 은닉층의 활성화 함수
z1 = sigmoid(a1)
# 은닉층에서 출력층으로의 선형 변환
a2 = np.dot(z1, w2) + b2
# 출력층의 활성화 함수 (소프트맥스)
y = softmax(a2)
return y
def loss(self, x, t):
# 입력 데이터 x와 정답 레이블 t를 받아서 손실값을 계산하는 메소드
y = self.predict(x) # 예측값을 구함
return cross_entropy_error(y, t) # 크로스 엔트로피 손실값을 반환
def score(self, x, t):
# 입력 데이터 x와 정답 레이블 t를 받아서 정확도를 계산하는 메소드
y = self.predict(x) # 예측값을 구함
y = np.argmax(y, axis=1) # 예측값에서 가장 큰 값을 가지는 인덱스(클래스)를 선택
t = np.argmax(t, axis=1) # 정답 레이블에서 가장 큰 값을 가지는 인덱스(클래스)를 선택
# 예측값과 정답값이 같은 비율을 계산하여 정확도를 반환
return np.sum(y == t) / len(x)
def fit(self, x, t):
# 입력 데이터 x와 정답 레이블 t를 받아서 파라미터를 학습하는 메소드
# 손실 함수의 기울기를 계산
loss = lambda i : self.loss(x, t) # 손실 함수 정의
grads = {}
# 파라미터에 대한 기울기를 계산
grads['w1'] = numerical_gradient(loss, self.params['w1'])
grads['b1'] = numerical_gradient(loss, self.params['b1'])
grads['w2'] = numerical_gradient(loss, self.params['w2'])
grads['b2'] = numerical_gradient(loss, self.params['b2'])
return grads
- 초기화: 네트워크의 파라미터를 설정합니다.
- 예측: 입력 데이터에 대해 예측값을 생성합니다.
- 손실: 예측값과 실제값의 차이를 계산합니다.
- 정확도: 모델의 성능을 평가합니다.
- 학습: 기울기를 계산하여 파라미터를 업데이트합니다.
신경망 모델의 학습과 평가를 수행
from tqdm import tqdm # for문의 진행상황을 시각적으로 표시
# My_Net 클래스의 인스턴스를 생성
# 입력층 4개 뉴런, 은닉층 8개 뉴런, 출력층 3개 뉴런을 가진 신경망
network = My_Net(4, 8, 3)
# 훈련 손실과 테스트 손실을 저장할 리스트를 초기화
train_losses = []
test_losses = []
# 1000번의 반복을 통해 모델을 학습
for i in tqdm(range(1000)): # 반복문 진행 상황을 표시하는 tqdm을 사용
# 무작위로 80개의 샘플을 선택하여 배치 데이터를 생성
mask = np.random.choice(112, 80)
x_batch = train_x[mask] # 선택된 샘플의 입력 데이터
t_batch = train_y[mask] # 선택된 샘플의 정답 레이블
# 현재 배치 데이터에 대해 기울기 계산
grad = network.fit(x_batch, t_batch)
# 각 파라미터에 대해 기울기를 사용하여 파라미터 업데이트
# 학습률(0.1)을 곱하여 파라미터 조정
for key in ('w1', 'b1', 'w2', 'b2'):
network.params[key] -= grad[key] * 0.1
# 전체 훈련 데이터와 테스트 데이터에 대한 손실값 계산
loss = network.loss(train_x, train_y) # 훈련 데이터 손실
test_loss = network.loss(test_x, test_y) # 테스트 데이터 손실
# 손실값을 리스트에 추가하여 기록
train_losses.append(loss)
test_losses.append(test_loss)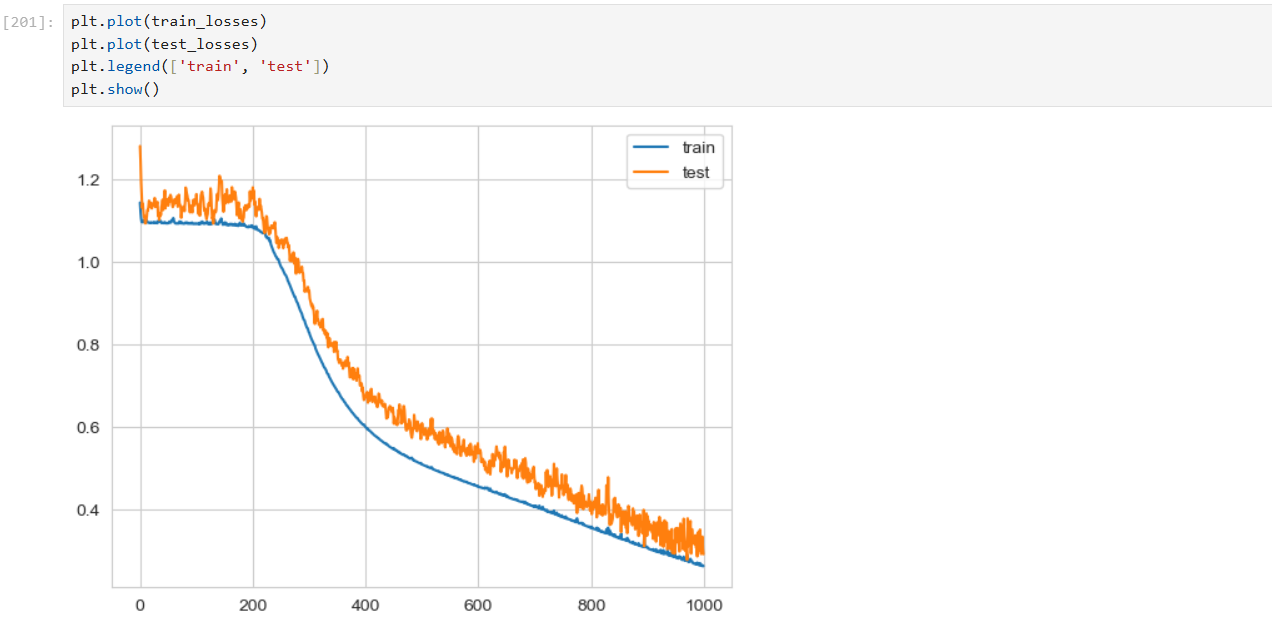
신경망 모델을 학습시키고, 학습 과정에서 손실값을 기록하여 모델의 성능을 평가하는 것
학습이 진행됨에 따라 train_losses와 test_losses에 저장된 값들을 분석하여 모델이 얼마나 잘 학습되었는지,
과적합이 발생했는지 등을 확인할 수 있다.
각 파라미터를 편미분
각 층을 미분 = 오차역전파
모멘텀 -> 아담
Pima Indians Diabetes 데이터셋을 이용한 신경망 모델 학습 및 평가
import pandas as pd
# 데이터셋을 로드
pima = pd.read_csv("/content/pima_indians.csv")
# 데이터와 레이블을 나누기
# 모든 열을 특성(X)으로, 'Class' 열을 레이블(Y)으로 설정
X = pima.iloc[:, :-1].to_numpy() # 모든 행과 마지막 열을 제외한 모든 열을 특성으로 설정
Y = pima['Class'].to_numpy() # 'Class' 열을 레이블로 설정
# 데이터를 훈련 세트와 테스트 세트로 분리
# 기본적으로 75%는 훈련 세트, 25%는 테스트 세트로 나누어짐
train_x, test_x, train_y, test_y = train_test_split(X, Y)
# 훈련 데이터의 평균과 표준편차를 계산
mean = train_x.mean(axis=0) # 각 특성의 평균을 계산
std = train_x.std(axis=0) # 각 특성의 표준편차를 계산
# 훈련 데이터와 테스트 데이터를 표준화
# 평균을 빼고 표준편차로 나누어 데이터 스케일링
train_scaled = (train_x - mean) / std
test_scaled = (test_x - mean) / std
# Keras 모델을 정의
model = keras.Sequential()
model.add(keras.layers.Dense(16, activation='sigmoid', input_shape=(8,))) # 입력층: 8개의 특성을 받아 16개의 뉴런을 가진 은닉층, 활성화 함수로 sigmoid 사용
model.add(keras.layers.Dense(2, activation='softmax')) # 출력층: 2개의 클래스에 대한 확률을 출력하는 소프트맥스 층
# 모델 컴파일
model.compile(loss="sparse_categorical_crossentropy", # 손실 함수: 희소 범주형 교차 엔트로피
metrics=['accuracy'], # 평가 지표: 정확도
optimizer='adam') # 옵티마이저: Adam
# 모델 훈련
# 훈련 데이터를 사용하여 모델을 학습시키고, 검증 데이터를 사용하여 모델 성능을 평가
hist = model.fit(train_scaled, train_y,
epochs=500, # 에포크 수: 500번의 반복
validation_data=(test_scaled, test_y)) # 검증 데이터: 테스트 데이터로 검증# 손실 시각화
plt.plot(history.history['loss'], label='Training Loss')
plt.plot(history.history['val_loss'], label='Validation Loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.title('Loss over Epochs')
plt.show()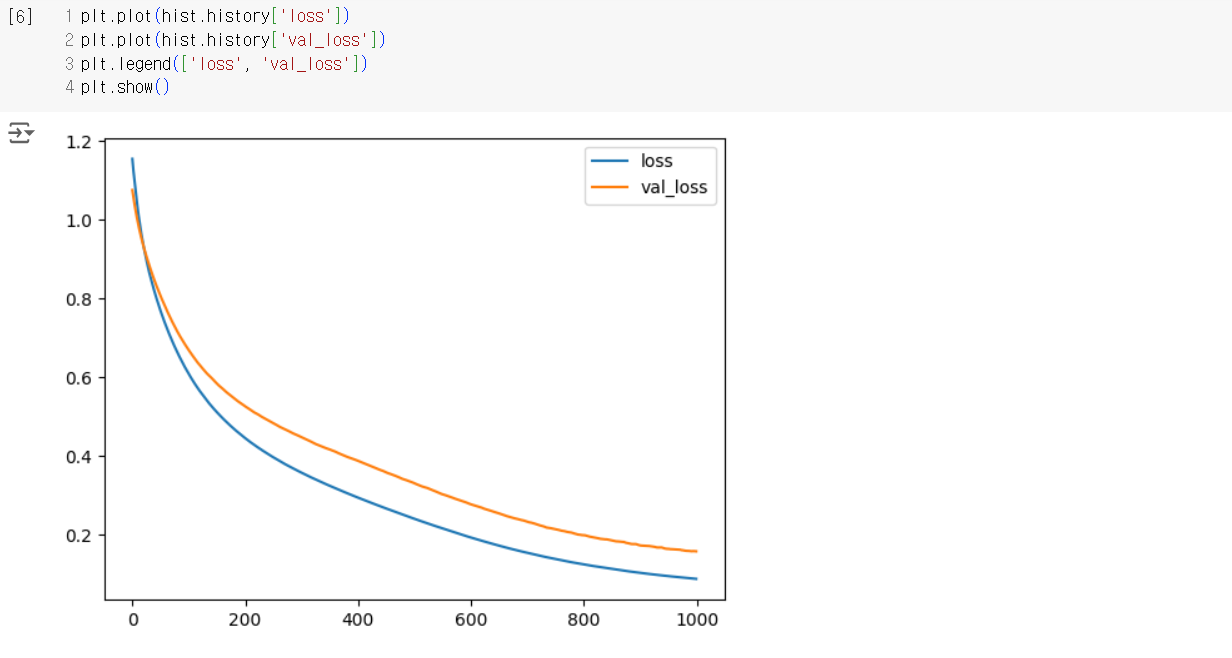
Pima Indians Diabetes 데이터셋을 활용한 다층 신경망 모델 학습
import pandas as pd
from sklearn.model_selection import train_test_split
from tensorflow import keras
# 데이터셋을 CSV 파일에서 읽어들임
pima = pd.read_csv("/content/pima_indians.csv")
# 특성과 레이블을 numpy 배열로 변환
X = pima.iloc[:, :-1].to_numpy() # 모든 행, 마지막 열을 제외한 모든 열(특성)
Y = pima['Class'].to_numpy() # 마지막 열(레이블)
# 데이터를 훈련 세트와 테스트 세트로 분리
train_x, test_x, train_y, test_y = train_test_split(X, Y)
# 훈련 데이터의 평균과 표준편차를 계산하여 표준화 작업
mean = train_x.mean(axis = 0) # 각 특성 열의 평균
std = train_x.std(axis = 0) # 각 특성 열의 표준편차
# 훈련 데이터와 테스트 데이터 표준화
train_scaled = (train_x - mean) / std
test_scaled = (test_x - mean) / std
# 신경망 모델 정의
model = keras.Sequential()
model.add(keras.layers.Dense(16, activation='relu', input_shape=(8,))) # 입력층과 첫 번째 은닉층 (16 뉴런, ReLU 활성화)
model.add(keras.layers.Dense(32, activation='relu')) # 두 번째 은닉층 (32 뉴런, ReLU 활성화)
model.add(keras.layers.Dense(32, activation='relu')) # 세 번째 은닉층 (32 뉴런, ReLU 활성화)
model.add(keras.layers.Dense(2, activation='softmax')) # 출력층 (2 뉴런, Softmax 활성화 - 이진 분류)
# 모델 컴파일
model.compile(loss="sparse_categorical_crossentropy", # 손실 함수: 희소 범주형 교차 엔트로피
metrics=['accuracy'], # 평가 지표: 정확도
optimizer='adam') # 최적화 알고리즘: Adam
# 모델 학습
hist = model.fit(train_scaled, train_y, # 훈련 데이터와 레이블
epochs=500, # 에포크 수 (500)
validation_data=(test_scaled, test_y)) # 검증 데이터
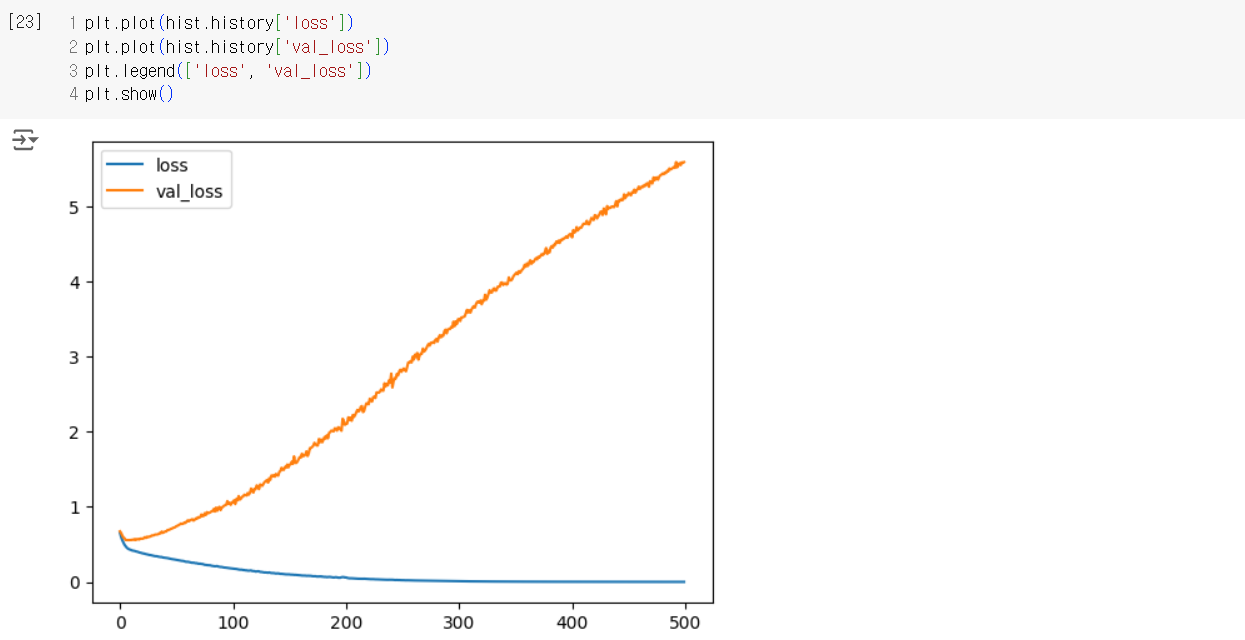
Pima Indians Diabetes 데이터셋을 사용한 딥러닝 모델 학습 (드롭아웃 포함)
import pandas as pd
from sklearn.model_selection import train_test_split
from tensorflow import keras
# 데이터셋을 CSV 파일에서 읽어들임
pima = pd.read_csv("/content/pima_indians.csv")
X = pima.iloc[:, :-1].to_numpy()
Y = pima['Class'].to_numpy()
train_x, test_x, train_y, test_y = train_test_split(X, Y)
mean = train_x.mean(axis = 0)
std = train_x.std(axis = 0)
train_scaled = (train_x - mean) / std
test_scaled = (test_x - mean) / std
model = keras.Sequential()
model.add(keras.layers.Dense(16, activation = 'relu', input_shape = (8,)))
model.add(keras.layers.Dropout(0.3)) # 16개의 은닉층에서 30%만큼 랜덤으로 꺼버린다.
model.add(keras.layers.Dense(32, activation = 'relu')) # relu 값을 온전하게 전달할 수 있음
model.add(keras.layers.Dropout(0.3))
model.add(keras.layers.Dense(32, activation = 'sigmoid')) # sigmoid 넣으면 어느정도 값 날리면서 전달
model.add(keras.layers.Dropout(0.3))
model.add(keras.layers.Dense(2, activation = 'softmax'))
model.compile(loss = "sparse_categorical_crossentropy",
metrics = ['accuracy'],
optimizer = 'adam')
hist = model.fit(train_scaled, train_y,
epochs = 500,
validation_data = (test_scaled, test_y))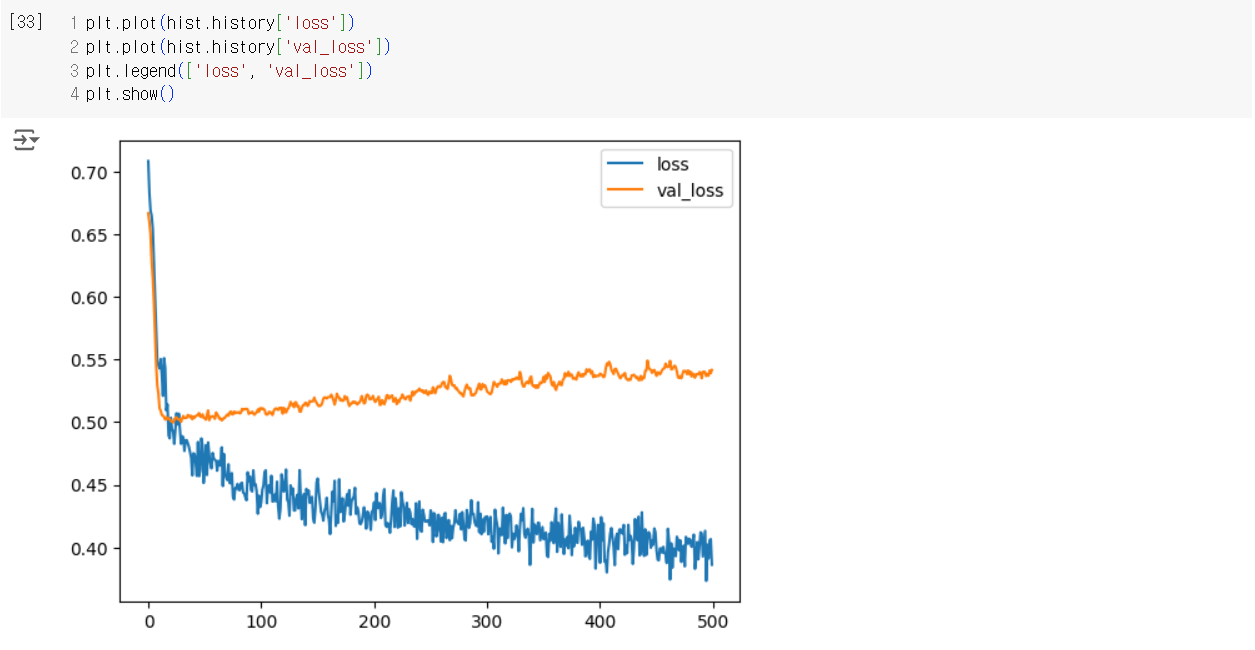
Pima Indians Diabetes Dataset을 이용한 신경망 모델 구축 및 조기 종료 적용
# 조기 종료를 위한 콜백 설정
es = keras.callbacks.EarlyStopping(patience=5, restore_best_weights=True)
import pandas as pd
from sklearn.model_selection import train_test_split
from tensorflow import keras
# 데이터셋을 CSV 파일에서 읽어들임
pima = pd.read_csv("/content/pima_indians.csv")
# 특성(X)과 레이블(Y)을 분리
X = pima.iloc[:, :-1].to_numpy() # 모든 열에서 마지막 열(레이블)을 제외한 데이터
Y = pima['Class'].to_numpy() # 레이블 열만 추출
# 훈련 세트와 테스트 세트로 데이터 분리
train_x, test_x, train_y, test_y = train_test_split(X, Y)
# 훈련 데이터의 평균과 표준편차를 계산하여 데이터 정규화
mean = train_x.mean(axis=0) # 각 특성의 평균
std = train_x.std(axis=0) # 각 특성의 표준편차
# 데이터 정규화: 평균을 빼고 표준편차로 나누어 스케일을 맞춤
train_scaled = (train_x - mean) / std
test_scaled = (test_x - mean) / std
# 신경망 모델 구축
model = keras.Sequential()
model.add(keras.layers.Dense(16, activation='relu', input_shape=(8,))) # 입력층: 8개의 특성, 은닉층: 16개의 뉴런, ReLU 활성화 함수
model.add(keras.layers.Dropout(0.3)) # Dropout 층: 30%의 뉴런을 랜덤하게 비활성화하여 과적합 방지
model.add(keras.layers.Dense(32, activation='relu')) # 은닉층: 32개의 뉴런, ReLU 활성화 함수
model.add(keras.layers.Dropout(0.3)) # Dropout 층: 30%의 뉴런을 랜덤하게 비활성화하여 과적합 방지
model.add(keras.layers.Dense(32, activation='sigmoid')) # 은닉층: 32개의 뉴런, Sigmoid 활성화 함수
model.add(keras.layers.Dropout(0.3)) # Dropout 층: 30%의 뉴런을 랜덤하게 비활성화하여 과적합 방지
model.add(keras.layers.Dense(2, activation='softmax')) # 출력층: 2개의 뉴런(이진 분류), Softmax 활성화 함수
# 조기 종료 콜백 설정: 5번의 에포크 동안 개선이 없으면 훈련을 중단하고 최적의 가중치로 복원
es = keras.callbacks.EarlyStopping(patience=5, restore_best_weights=True)
# 모델 컴파일: 손실 함수는 sparse_categorical_crossentropy, 최적화기는 adam, 평가 지표로 accuracy 사용
model.compile(loss="sparse_categorical_crossentropy",
metrics=['accuracy'],
optimizer='adam')
# 모델 훈련: 500 에포크 동안 훈련, 검증 데이터로 test_scaled와 test_y 사용, 조기 종료 콜백 적용
hist = model.fit(train_scaled, train_y,
epochs=500,
validation_data=(test_scaled, test_y),
callbacks=[es])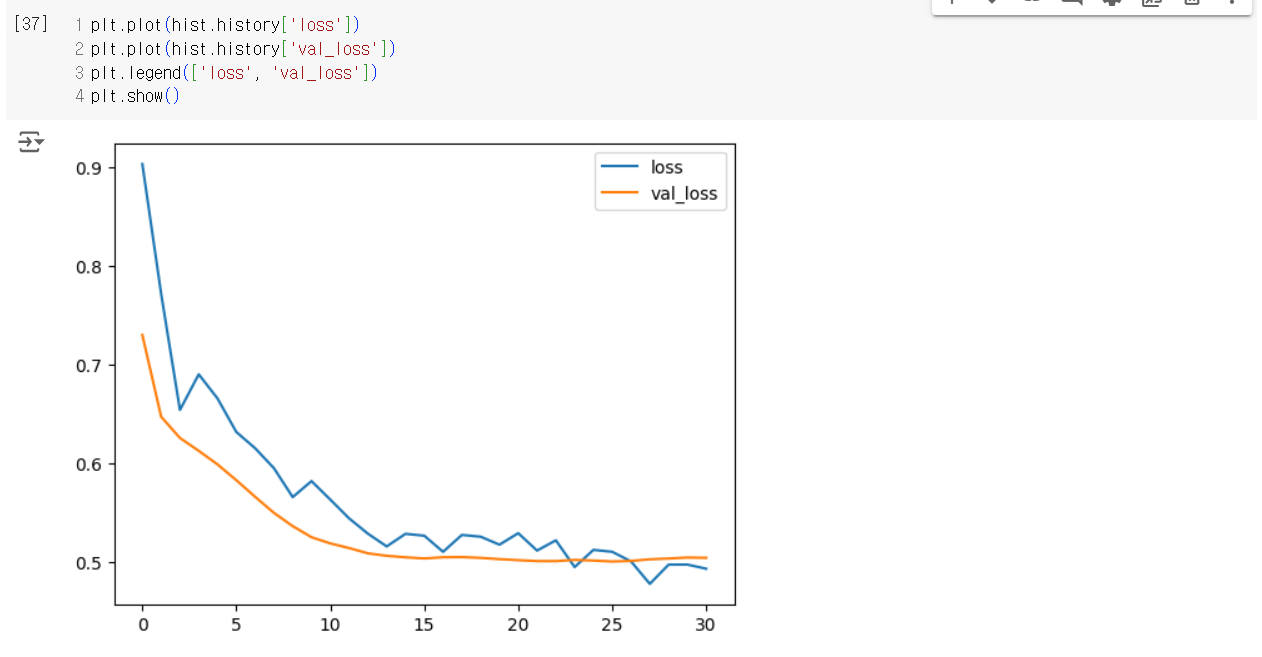
'파이썬 & 머신러닝과 딥러닝' 카테고리의 다른 글
| 오차역전파법, 미분과 체인룰, 브로드캐스팅, 텐서 조작 (2) | 2024.09.03 |
|---|---|
| AutoML, 퍼셉트론, 다층 퍼셉트론(MLP) (14) | 2024.09.02 |
| 인공신경망, 지도학습, 회귀모델 (0) | 2024.08.20 |
| 로지스틱 회귀, K-Fold 교차 검증, 비복원추출, 배깅(랜덤 포레스트), 부스팅(AdaBoost, Gradient Boosting), XGBoost (0) | 2024.08.12 |
| SVM, K-means 클러스터링, 의사결정나무, 로지스틱회귀 (1) | 2024.08.12 |



