분류 모델
공부시간으로 성적 예측

np.array에 넣으면 행렬로 바껴서 각각의 리스트 원소에 더하기 가능해짐
np.array로 행렬로 바꿔주기
a = a - a' 를 했을때 순간기울기가 0이 되는 지점이 생기는데
0이 되는 지점에서는 더이상 학습해도 소용 없다는걸 알 수 있음
그걸 대입하면 직선의 방정식 기울기를 알 수 있음


3000 번 학습시키기

오차를 출력하고 순간 기울기를 구하는 과정
→ 파라미터(a1, b)의 기울기가 0에 가까워지면 손실 함수가 최적화된 상태


오차가 최소가 되는 지점(손실 함수의 값이 최소가 되는 지점, 평균 제곱 오차(MSE)) 를 확인할 수 있음.
회귀선이 데이터 포인트와 가까울수록 손실 함수 값이 최소화되었다고 볼 수 있다.
두 개의 입력 특성 x1 (공부시간)과 x2 (문제집 푼 개수)로부터 y (성적) 예측
y = a1x1 + a2x2 + b로 만들어보기
특성이 늘어나면 굴곡이 생김
import numpy as np
import matplotlib.pyplot as plt
# 데이터
x1 = np.array([2, 4, 6, 8]) # 공부시간
x2 = np.array([1, 2, 1, 3]) # 문제집 푼 개수
y = np.array([20, 55, 45, 80]) # 성적
# 초기값
a1 = 0
a2 = 0
b = 0
lr = 0.001 # 학습률
# 학습 과정
for i in range(3000): # 3000번 학습
y_hat = a1 * x1 + a2 * x2 + b # 예측값
error = y_hat - y # 오차
# 기울기 계산
a1_diff = 2 * np.sum(error * x1) # a1의 편미분값
a2_diff = 2 * np.sum(error * x2) # a2의 편미분값
b_diff = 2 * np.sum(error) # b의 편미분값
# 파라미터 업데이트
a1 = a1 - lr * a1_diff
a2 = a2 - lr * a2_diff # 수정된 부분
b = b - lr * b_diff
# 학습 과정 출력
print(f'{i+1}회 학습 / a1: {a1:.2f}, a2: {a2:.2f}, b: {b:.2f}')


→ 주어진 데이터와 모델의 파라미터를 업데이트하여 예측값과 실제값 간의 오차를 최소화
1. sin 그래프와 가장 오차가 작은 직선 그리기
# 1. sin 그래프와 가장 오차가 작은 직선 그리기
# 2. sin 그래프와 가장 오차가 작은 2차 함수 그래그 그리기
# 데이터 생성
x = np.arange(-3, 3, 0.01) # x 값 생성
y = np.sin(x) # sin(x) 값을 계산
# 초기값 설정
a = 0 # 기울기 초기값
b = 0 # 절편 초기값
lr = 0.0001 # 학습률 설정
# 경사 하강법 학습
for i in range(5000): # 1000번 반복
y_hat = a * x + b # 예측값 계산
error = y_hat - y # 오차 계산
# 기울기 계산
a_diff = sum(2 * error * x) # 기울기 a의 편미분값
b_diff = sum(2 * error * 1) # 기울기 b의 편미분값
# 파라미터 업데이트
a = a - lr * a_diff # 기울기 a 업데이트
b = b - lr * b_diff # 절편 b 업데이트
print(f'{i+1}회 학습 / a 기울기 : {a_diff:.2f}, b 기울기 :{b_diff:.2f}')

2. sin 그래프와 가장 오차가 작은 2차 함수 그래프 그리기
# 1. sin 그래프와 가장 오차가 작은 직선 그리기
# 2. sin 그래프와 가장 오차가 작은 2차 함수 그래프 그리기 (O)
x = np.arange(-3, 3, 0.01)
y = np.sin(x)
a = 0
b = 0
c = 0
lr = 0.00005
for i in range(5000):
y_hat = a * x ** 2 + b * x + c
error = y_hat - y
a_diff = sum(2 * error * x ** 2)
b_diff = sum(2 * error * x)
c_diff = sum(2 * error * 1)
a -= a_diff * lr
b -= b_diff * lr
c -= c_diff * lr
print(f"{a_diff:.2f}, {b_diff:.2f}, {c_diff:.2f}")


3. sin 그래프와 가장 오차가 작은 3차 함수 그래프 그리기
# 1. sin 그래프와 가장 오차가 작은 직선 그리기
# 2. sin 그래프와 가장 오차가 작은 2차 함수 그래프 그리기 (O)
x = np.arange(-3, 3, 0.01)
y = np.sin(x)
a = 0
b = 0
c = 0
d = 0
lr = 0.000005
for i in range(5000):
y_hat = a * x ** 3 + b * x ** 2 + c * x + d
error = y_hat - y
a_diff = sum(2 * error * x ** 3)
b_diff = sum(2 * error * x ** 2)
c_diff = sum(2 * error * x)
d_diff = sum(2 * error * 1)
a -= a_diff * lr
b -= b_diff * lr
c -= c_diff * lr
d -= d_diff * lr
print(f"{a_diff:.2f}, {b_diff:.2f}, {c_diff:.2f}, {d_diff:.2f}")

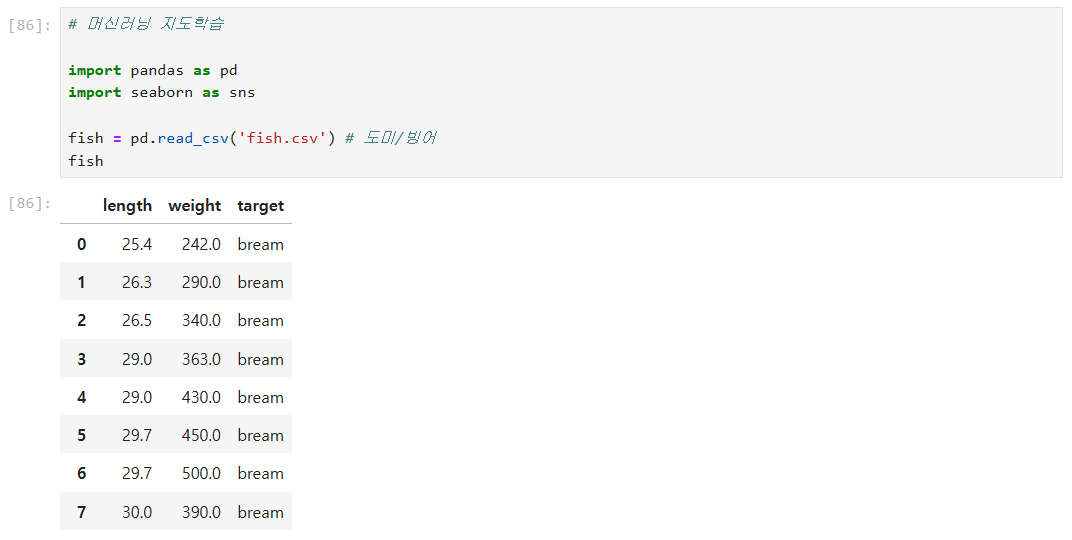
머신러닝 지도학습




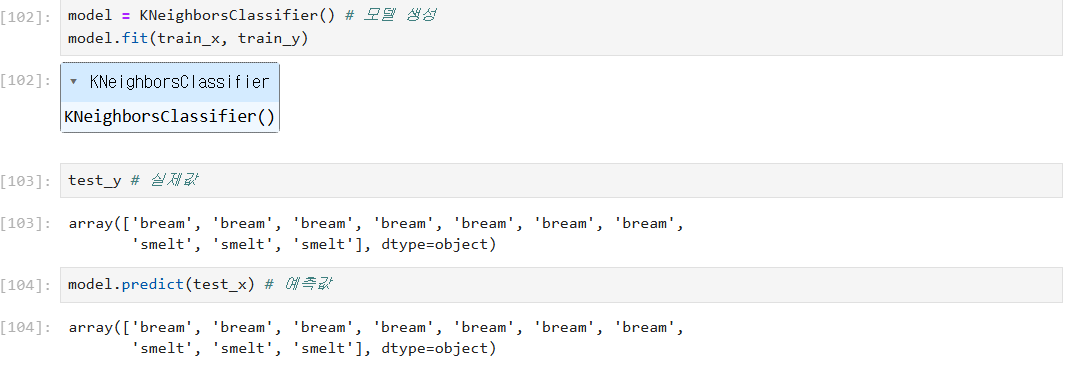

→ 컴퓨터가 모르는 데이터를 다 맞힌 상태(1.0)

→ 잘 학습된 모델인데 틀린 모습을 보임 (도미인데 빙어라고 나옴)



→ 주황 표시를 예측해야하는데 초록색 다수결로 빙어로 잘못 예측된 걸 알 수 있다.

→ 훈련데이터를 통해 알 수 있는 평균과 표준편차를 통해 예측을 해야함
→ 훈련데이터에도 평균을 뺌 (데이터 표준)
→ 평균을 빼고 표준편차로 나누어 표준화 (안되는 경우 중앙값 빼기)

→ 모델 만들고 데이터 표준화해서 잘 학습되었다고 나온 모습

→ 도미라고 이제는 잘 예측된 모습

fish2.csv(7종류의 생선 / 5개의 특성)


→ score 0.675
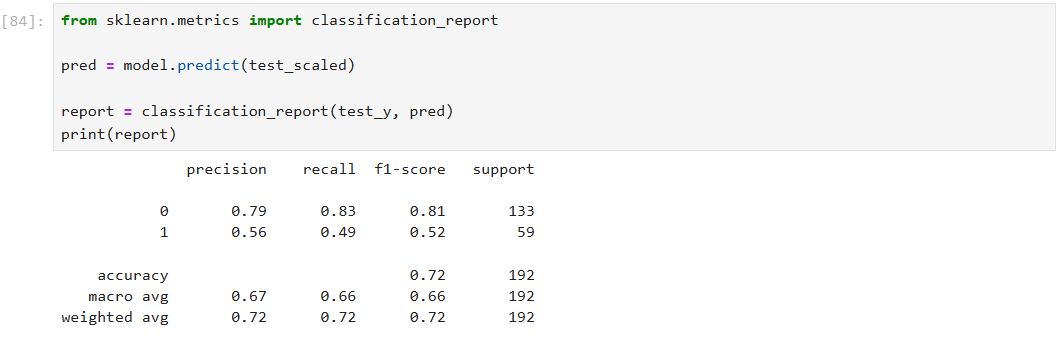
각각의 이웃숫자마다 성능을 출력


- 정밀도는 모델이 양성으로 예측한 것 중에서 몇 개가 실제로 양성이었는가?
- 정확도는 모델이 전체 샘플 중에서 얼마나 많이 맞췄는가?
- 재현율은 실제 양성인 것 중에서 모델이 양성으로 정확히 예측한 비율

회귀모델
K 최근접 이웃 회귀 모델
연속된 모델 예측시 회귀모델 사용



비정형데이터 : 딥러닝
정형데이터
- 데이터 균형하고 많다/적다 = 랜덤포레스트
- 데이터가 불균형한데 많다 = XGboost(오차가 많을수록 잘 학습)
- 데이터가 불균형한데 적다 = 서포트 벡터 머신
정형 데이터 : 트리 기반(결정트리, 랜덤포레스트, XGBoost)
1. 쉽다 (데이터 표준화 -> 연산 X)
2. 강력함
3. 데이터의 설명력을 가짐


훈련 >>>>>>> 시험 : 과대 적합
훈련 > 시험 : 0000
훈련 < 시험 : 과소적합 의심
둘 다 작게 나오는 경우 : 과소적합
랜덤포레스트(결졍트리 100개) > 결정트리
1. 데이터 분할(정확도만 볼거라면)
2. 과대적합에 강함.

랜덤포레스트(배깅)
→ XGBoost(부스팅) : 약한 학습기(찍는 것 보단 나은 모델)를 활용해서 학습

'파이썬 & 머신러닝과 딥러닝' 카테고리의 다른 글
| AutoML, 퍼셉트론, 다층 퍼셉트론(MLP) (14) | 2024.09.02 |
|---|---|
| R^2, 부스팅, 퍼셉트론, 시그모이드, 소프트맥스 함수, 크로스엔트로피 손실, 신경망 모델 (0) | 2024.08.27 |
| 로지스틱 회귀, K-Fold 교차 검증, 비복원추출, 배깅(랜덤 포레스트), 부스팅(AdaBoost, Gradient Boosting), XGBoost (0) | 2024.08.12 |
| SVM, K-means 클러스터링, 의사결정나무, 로지스틱회귀 (1) | 2024.08.12 |
| 데이터 정규화, 표준화, 백분위수, 주성분 분석 (PCA), 회귀분석, 회귀 성능 평가(MAE, MSE, RMSE, R² 스코어) (0) | 2024.08.08 |



