샘플링 방법
- 복원추출 (replacement): 샘플을 추출한 후, 다시 원래 집합에 돌려놓고 다음 샘플을 추출하는 방법 (같은 요소가 여러 번 선택 가능)
- 비복원추출 (non-replacement): replace=False 추가, 샘플을 추출한 후, 다시 원래 집합에 돌려놓지 않고 다음 샘플을 추출하는 방법( 같은 요소가 한 번만 선택됨 )
랜덤 시드값 세팅
시드 값 0을 사용한 경우, np.random.choice가 난수를 생성하는 순서가 항상 동일하게 됨
import numpy as np
print(np.random.choice([1,2,3], 3))
# 비복원추출
print(np.random.choice([1,2,3], 3, replace=False))
# 랜덤 시드값 세팅
np.random.seed(0)
print(np.random.choice([1,2,3], 3))

csv 파일을 불러와 numpy 배열로 변환
import pandas as pd
import numpy as np
df = pd.read_csv('C:/Users/campus4D033/ch4_scores400.csv')
# numpy의 array 함수를 호출하여 DataFrame을 배열로
df_narray1 = np.array(df['score'])
# pandas DataFrame 객체의 메서드를 호출하여 배열로 변환
df_narray2 = df['score'].to_numpy()
print(df_narray1)
print(df_narray2)
확률분포 구하기
주어진 확률 분포에 따라 주사위 던지기를 100번 수행한 후 각 시도에서 나온 주사위 숫자 나타내기
dice1 = [1,2,3,4,5,6]
# 각 면이 나올 확률
dice2 = [1/21, 2/21, 3/21, 4/21, 5/21, 6/21]
# dice2의 확률분포 구하기
trial = 100 # 시도 횟수
# dice1에서 100개의 값을 dice2의 확률에 따라 선택
sample = np.random.choice(dice1, trial, p = dice2)
print(sample)

히스토그램 그리기
주사위 면마다 직접 지정한 확률 분포(dice2)를 기반으로 시뮬레이션을 수행
import numpy as np
import matplotlib.pyplot as plt
dice1 = [1,2,3,4,5,6]
# 각 면이 나올 확률
dice2 = [1/21, 2/21, 3/21, 4/21, 5/21, 6/21]
# dice2의 확률분포 구하기
trial = 100 # 시도 횟수
# dice1에서 100개의 값을 dice2의 확률에 따라 선택
sample = np.random.choice(dice1, trial, p = dice2)
print(sample)
# 주어진 샘플값으로 히스토그램 그리기
plt.hist(sample, bins=np.arange(1, 8) - 0.5, density=True, edgecolor='black')
# 히스토그램 설정
plt.xticks(dice1)
plt.xlabel('Dice Face')
plt.ylabel('Frequency')
plt.title('Histogram of Dice Rolls')
# 히스토그램 출력
plt.show()

데이터셋에서 점수 데이터(scores)를 읽어와 해당 데이터의 분포를 히스토그램으로 나타내기
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# 데이터 파일 읽기
df = pd.read_csv('C:/Users/campus4D033/ch4_scores400.csv')
# 'score' 열 데이터를 numpy 배열로 변환
scores = np.array(df['score'])
# 주사위 면과 각 면이 나올 확률 설정
dice1 = [1,2,3,4,5,6]
dice2 = [1/21, 2/21, 3/21, 4/21, 5/21, 6/21]
# 시도 횟수 설정
trial = 100
# 주사위 시뮬레이션 실행
sample = np.random.choice(dice1, trial, p=dice2)
# 히스토그램 그리기
fig = plt.figure(figsize=(10, 6)) # 플롯을 생성할 Figure 객체 생성, 크기는 가로 10인치, 세로 6인치
ax = fig.add_subplot(111) # Figure 객체에 서브플롯(axes)을 추가 (1x1 그리드에서 첫 번째(111) 위치에 추가)
ax.hist(scores, bins=100, range=(0,100), density=True)
ax.set_xlim(20, 100) # x 축 범위 설정
ax.set_ylim(0, 0.042) # y 축 범위 설정
ax.set_xlabel('score') # x 축 레이블 설정
ax.set_ylabel('re_freq') # y 축 레이블 설정
plt.show() # 플롯 출력

모평균을 세로선으로 표현
ax.vlines(np.mean(scores), 0, 1, 'gray') 추가
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# 데이터 파일 읽기
df = pd.read_csv('C:/Users/campus4D033/ch4_scores400.csv')
# 'score' 열 데이터를 numpy 배열로 변환
scores = np.array(df['score'])
score_means = [np.random.choice(scores, 20).mean() for _ in range(1000)]
# 히스토그램 그리기
fig = plt.figure(figsize=(10, 6)) # 플롯을 생성할 Figure 객체 생성, 크기는 가로 10인치, 세로 6인치
ax = fig.add_subplot(111) # Figure 객체에 서브플롯(axes)을 추가 (1x1 그리드에서 첫 번째(111) 위치에 추가)
ax.hist(scores, bins=100, range=(0,100), density=True)
ax.vlines(np.mean(scores), 0, 1, 'gray')
ax.set_xlim(20, 100) # x 축 범위 설정
ax.set_ylim(0, 0.042) # y 축 범위 설정
ax.set_xlabel('score') # x 축 레이블 설정
ax.set_ylabel('re_freq') # y 축 레이블 설정
plt.show() # 플롯 출력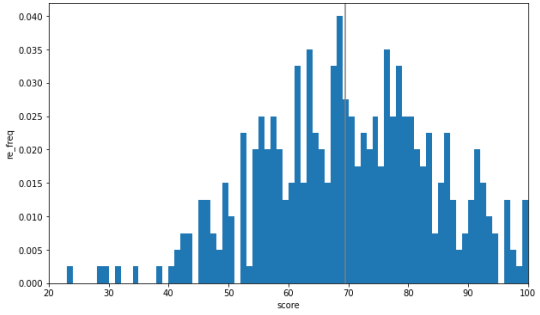
dice2를 확률값(소수)으로 나오게 하기
# 확률값으로 나오게 하기 2
x_set = np.array([1,2,3,4,5,6])
def f(x):
if x in x_set:
return x/21
else:
return 0
x_in = [x_set, f]
prob = np.array([f(x_k) for x_k in x_set ])
print(prob)
dice_dict = dict(zip(x_set, prob))
print(dice_dict)
어떤 확률분포 값이 높게 나오는지 확인하기
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# 데이터 파일 읽기
df = pd.read_csv('C:/Users/campus4D033/ch4_scores400.csv')
# 'score' 열 데이터를 numpy 배열로 변환
scores = np.array(df['score'])
# 확률값으로 나오게 하기
x_set = np.array([1,2,3,4,5,6])
def f(x):
if x in x_set:
return x/21
else:
return 0
x_in = [x_set, f]
prob = np.array([f(x_k) for x_k in x_set ])
print(prob)
data = dict(zip(x_set, prob))
print(data)
x_data = list(data.keys())
y_data = list(data.values())
fig, ax = plt.subplots(figsize=(8,5))
# 히스토그램 그리기
ax.bar(x_data, y_data, width=0.5, align = 'center', alpha = 0.7)
# 축과 레이블 설정
ax.set_xlabel('number')
ax.set_ylabel('prob')
ax.set_title('Histogram of Scores with Prob')

확률변수의 평균값(기대값) 구하기
- print(np.sum([x_k * f(x_k) for x_k in x_set]))
- sample = np.random.choice(x_set, int(1e6), p = prob)
import numpy as np
import pandas as pd
# 데이터 파일 읽기
df = pd.read_csv('C:/Users/campus4D033/ch4_scores400.csv')
# 'score' 열 데이터를 numpy 배열로 변환
scores = np.array(df['score'])
x_set = np.array([1,2,3,4,5,6])
def f(x):
if x in x_set:
return x/21
else:
return 0
x_in = [x_set, f]
prob = np.array([f(x_k) for x_k in x_set ])
# 기대값 구하기 1
print(np.sum([x_k * f(x_k) for x_k in x_set]))
# 기대값 구하기 2 (실제 현장에서 사용)
score_means = [np.random.choice(scores, 20)]
sample = np.random.choice(x_set, int(1e6), p = prob)
# 1e6 : 1000000번
print(sample.mean())
데이터 편향을 제거하기 위해 셔플 진행
람다 함수(lambda function)
파이썬에서 간단한 함수를 한 줄로 정의할 수 있는 방법
일반적인 함수와 달리 이름을 갖지 않고, 한 줄로 작성하여 사용 가능
람다 함수의 기본 구조
lambda arguments: expression
add = lambda x, y: x + y
람다함수로 분산 구하기
# -*- coding: utf-8 -*-
"""
Created on Tue Jul 2 13:12:19 2024
@author: campus4D033
"""
import numpy as np
def f(x):
if x in x_set:
return x/21
else:
return 0
#mean = E(X)
np.sum([])
x_set = np.array([1,2,3,4,5,6])
x_in = [x_set, f]
def E(X, g=lambda x: x):
x_set, f = X
return np.sum(g(x_k) * f(x_k) for x_k in x_set)
E(x_in, g=lambda x: 2*x + 3)
# 2 ** 2 V(X) = V(2X +3)
def V(X, g=lambda x: x):
x_set, f = X
mean = E(X, g)
return np.sum([(g(x_k)-mean) ** 2 * f(x_k) for x_k in x_set])
print(V(x_in, lambda x:2*x +3))
mean = E(x_in)
히트맵 ( heatmap )
x, y 2차원 확률 분포를 히트맵으로 시각화
import numpy as np
import matplotlib.pyplot as plt
x_set = np.arange(2, 13)
y_set = np.arange(1, 7)
# 확률값 계산
def f_XY(x, y) :
if 1<=y<=6 and 1<=x-y<=6:
return y * (x-y) / 100
else :
return 0
# XY 배열과 확률값 계산 함수 정의
XY = [x_set, y_set, f_XY]
# 각 (x_i, y_j)에 대해 확률값을 계산하여 prob 배열에 저장
prob = np.array([[f_XY(x_i, y_j) for y_j in y_set] for x_i in x_set])
# 히트맵을 그릴 Figure 객체 생성
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111)
# 히트맵 그리기
c = ax.pcolor(prob)
ax.set_xticks(np.arange(prob.shape[1]) + 0.5, minor=False) # 열값 기준
ax.set_yticks(np.arange(prob.shape[0]) + 0.5, minor=False)
# 라벨값 세팅
ax.set_xticklabels(np.arange(1, 7), minor=False)
ax.set_yticklabels(np.arange(2, 13), minor=False)
# y축을 뒤집고, x축을 상단에 배치
ax.invert_yaxis()
ax.xaxis.tick_top()
# 색상 막대(colorbar) 추가
fig.colorbar(c, ax=ax)
plt.show()
주변 확률분포값 추가 + x, y에 대한 기대값 구하기 + 분산 + 공분산
x에 대한 주변 확률분포(marginal probability distribution of xx)
다변량 확률분포에서 특정 변수 xx의 값만 고려했을 때의 확률분포
다른 변수 yy의 값을 모두 무시하고 xx의 값에 대한 전체적인 확률을 나타냄
분산은 하나의 변수의 변동성을 측정
공분산은 두 변수 간의 변동성을 측정.
-> 분산은 데이터가 평균으로부터 얼마나 퍼져 있는지를 나타내며,
공분산은 두 변수가 어떻게 함께 변하는지를 나타냄
import numpy as np
import matplotlib.pyplot as plt
x_set = np.arange(2, 13)
y_set = np.arange(1, 7)
# 확률값 계산
def f_XY(x, y) :
if 1<=y<=6 and 1<=x-y<=6:
return y * (x-y) / 100
else :
return 0
# XY 배열과 확률값 계산 함수 정의
XY = [x_set, y_set, f_XY]
# 각 (x_i, y_j)에 대해 확률값을 계산하여 prob 배열에 저장
prob = np.array([[f_XY(x_i, y_j) for y_j in y_set] for x_i in x_set])
# 히트맵을 그릴 Figure 객체 생성
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111)
# 히트맵 그리기
c = ax.pcolor(prob)
ax.set_xticks(np.arange(prob.shape[1]) + 0.5, minor=False) # 열값 기준
ax.set_yticks(np.arange(prob.shape[0]) + 0.5, minor=False)
# 라벨값 세팅
ax.set_xticklabels(np.arange(1, 7), minor=False)
ax.set_yticklabels(np.arange(2, 13), minor=False)
# y축을 뒤집고, x축을 상단에 배치
ax.invert_yaxis()
ax.xaxis.tick_top()
# 색상 막대(colorbar) 추가
fig.colorbar(c, ax=ax)
plt.show()
print(np.all(prob >= 0))
# x에 대한 주변 확률분포값 확인
def f_X(x):
return np.sum([f_XY(x,y_k) for y_k in y_set])
# y에 대한 주변 확률분포값 확인
def f_Y(y):
return np.sum(f_XY(x_k, y) for x_k in x_set)
X = [x_set, f_X]
Y = [y_set, f_Y]
prob_x = np.array([f_X(x_k) for x_k in x_set])
prob_y = np.array([f_Y(y_k) for y_k in y_set])
# 히스토그램 그리기
fig = plt.figure(figsize=(12,8)) # 플롯을 생성할 Figure 객체 생성, 크기는 가로 10인치, 세로 6인치
ax1 = fig.add_subplot(121) # Figure 객체에 서브플롯(axes)을 추가 (1x1 그리드에서 첫 번째(111) 위치에 추가)
ax2 = fig.add_subplot(122)
ax1.bar(x_set, prob_x)
ax1.set_title('x-marginal probability dist.')
ax1.set_xlabel('x_value') # x 축 레이블 설정
ax1.set_ylabel('probability') # y 축 레이블 설정
ax2.bar(y_set, prob_y)
ax2.set_title('y-marginal probability dist.')
ax2.set_xlabel('y_value') # x 축 레이블 설정
ax2.set_ylabel('probability') # y 축 레이블 설정
plt.show() # 플롯 출력
# X와 Y의 모든 가능한 조합에 대해 𝑥𝑖와 그에 대응하는 확률값을 곱하고, 이를 모두 더한 값을 출력
print(np.sum([x_i * f_XY(x_i, y_j) for x_i in x_set for y_j in y_set]))
# 함수로 위 print문을 만들고 기대값 구하기
def E(X, g):
x_set, y_set, f_XY = XY
return np.sum([g(x_i, y_j) * f_XY(x_i, y_j) for x_i in x_set for y_j in y_set])
mean_x = E(XY, lambda x, y : x)
print(mean_x)
mean_y = E(XY, lambda x, y : y)
print(mean_y)
# x에 대한 분산값
np.sum([(x_i-mean_x) ** 2 * f_XY(x_i, y_j) for x_i in x_set for y_j in y_set])
# y에 대한 분산값
np.sum([(y_j-mean_y) ** 2 * f_XY(x_i, y_j) for x_i in x_set for y_j in y_set])
# 주어진 이변량 확률분포 XY와 함수 g에 대해 분산을 계산
def V2(XY, g):
x_set, y_set, f_XY = XY
mean = E(XY, g)
return np.sum([(g(x_i, y_j) - mean) ** 2 * f_XY(x_i, y_j) for x_i in x_set for y_j in y_set])
# 이변량 확률분포 XY에 대해 공분산을 계산
def Cov(XY):
x_set, y_set, f_XY = XY
mean_x = E(XY, lambda x, y: x)
mean_y = E(XY, lambda x, y: y)
return np.sum([(x_i-mean_x) * (y_j-mean_y) * f_XY(x_i, y_j) for x_i in x_set for y_j in y_set])
# 중첩 for문
cov_xy = Cov(XY)
print(cov_xy)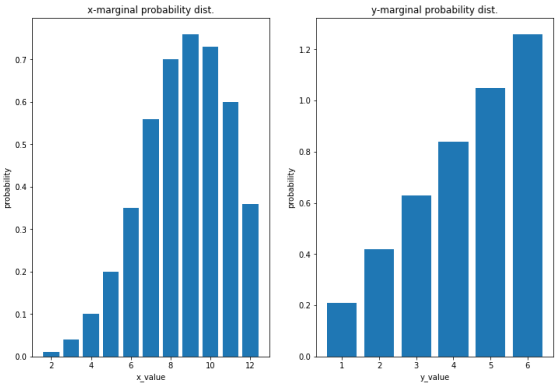
상관계수
두 변수 와 의 상관계수를 계산
이 공식은 표준화된 공분산으로, 두 변수의 단위가 다를 경우에도 비교할 수 있게 해줌
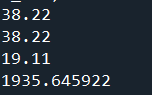
# x, y에 대한 공분산 값 계산
var_x = V2(XY, g = lambda x, y : x)
var_y = V2(XY, g = lambda x, y : y)
cov_xy = Cov(XY)
# 두 변수 X와 Y의 상관계수를 계산
print(cov_xy / np.sqrt(var_x * var_y))
베르누이 분포와 이항 분포를 구현하고 시각화
베르누이 분포
: 이항 분포의 특수한 경우로, 단순히 성공(1) 또는 실패(0) 두 가지 결과만을 가지는 경우에 해당
베르누이 분포와 이항 분포를 정의하고, 해당 확률 분포의 기댓값, 분산을 계산하며 검증하고 시각화
# -*- coding: utf-8 -*-
"""
Created on Tue Jul 2 15:26:48 2024
@author: campus4D033
"""
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
# 그래프 선의 종류
linestyles = ['-', '--', ':']
# 확률 변수 X의 기댓값과 분산을 계산하고 확인하는 함수들을 정의
def E(X, g=lambda x: x):
x_set, f = X
return np.sum([g(x_k) * f(x_k) for x_k in x_set])
def V(X, g=lambda x: x):
x_set, f = X
mean = E(X, g)
return np.sum([(g(x_k)-mean)**2 * f(x_k) for x_k in x_set])
def check_prob(X):
x_set, f = X
prob = np.array([f(x_k) for x_k in x_set])
assert np.all(prob >= 0), 'minus probability'
prob_sum = np.round(np.sum(prob), 6)
assert prob_sum == 1, f'sum of probability{prob_sum}'
print(f'expected value {E(X):.4}')
print(f'variance {(V(X)):.4}')
def plot_prob(X):
x_set, f = X
prob = np.array([f(x_k) for x_k in x_set])
fig = plt.figure(figsize=(10, 6))
ax = fig.add_subplot(111)
ax.bar(x_set, prob, label='prob')
ax.vlines(E(X), 0, 1, label='mean')
ax.set_xticks(np.append(x_set, E(X)))
ax.set_ylim(0, prob.max()*1.2)
ax.legend()
plt.show()
# 베르누이 분포
def Bern(p):
x_set = np.array([0, 1])
def f(x):
if x in x_set:
return p ** x * (1-p) ** (1-x)
else:
return 0
return x_set, f
p = 0.3
X = Bern(p)
check_prob(X)
plot_prob(X)
from scipy.stats import bernoulli
vr = bernoulli(p)
print(vr.pmf(0), vr.pmf(1))
print(vr.cdf([0, 1]))
print(vr.mean()) # 평균값
print(vr.var()) # 분
# 이항분포
from scipy.special import comb
def Bin(n, p):
x_set = np.arange(n+1)
def f(x):
if x in x_set:
return comb(n, x) * p ** x * (1-p) ** (n-x)
else:
return 0
return x_set, f
n = 10
X = Bin(n, p)
check_prob(X)
plot_prob(X)
fig = plt.figure(figsize=(10, 6))
ax = fig.add_subplot(111)
x_set = np.arange(n+1)
for p, ls in zip([0.3, 0.5, 0.7], linestyles):
rv = stats.binom(n, p)
ax.plot(x_set, rv.pmf(x_set),
label=f'p:{p}', ls=ls, color='gray')
ax.set_xticks(x_set)
ax.legend()
plt.show()

기하분포
: 주어진 확률 로 첫 번째 성공이 일어날 때까지의 독립적인 베르누이 시행을 나타내는 확률 분포
( 기하 분포는 이항 분포의 특수한 경우로, 성공 확률 이 매우 작은 경우에는 평균적으로 많은 시행이 필요
반면에 이 크면 상대적으로 적은 시행으로도 첫 번째 성공을 기대할 수 있음 )
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
# 그래프 선의 종류
linestyles = ['-', '--', ':']
# 확률 변수 X의 기댓값과 분산을 계산하고 확인하는 함수들을 정의
def E(X, g=lambda x: x):
x_set, f = X
return np.sum([g(x_k) * f(x_k) for x_k in x_set])
def V(X, g=lambda x: x):
x_set, f = X
mean = E(X, g)
return np.sum([(g(x_k)-mean)**2 * f(x_k) for x_k in x_set])
def check_prob(X):
x_set, f = X
prob = np.array([f(x_k) for x_k in x_set])
assert np.all(prob >= 0), 'minus probability'
prob_sum = np.round(np.sum(prob), 6)
assert prob_sum == 1, f'sum of probability{prob_sum}'
print(f'expected value {E(X):.4}')
print(f'variance {(V(X)):.4}')
def plot_prob(X):
x_set, f = X
prob = np.array([f(x_k) for x_k in x_set])
fig = plt.figure(figsize=(10, 6))
ax = fig.add_subplot(111)
ax.bar(x_set, prob, label='prob')
ax.vlines(E(X), 0, 1, label='mean')
ax.set_xticks(np.append(x_set, E(X)))
ax.set_ylim(0, prob.max()*1.2)
ax.legend()
plt.show()
# 베르누이 분포
def Bern(p):
x_set = np.array([0, 1])
def f(x):
if x in x_set:
return p ** x * (1-p) ** (1-x)
else:
return 0
return x_set, f
p = 0.3
X = Bern(p)
check_prob(X)
plot_prob(X)
from scipy.stats import bernoulli
vr = bernoulli(p)
print(vr.pmf(0), vr.pmf(1))
print(vr.cdf([0, 1]))
print(vr.mean()) # 평균값
print(vr.var()) # 분
from scipy.special import comb
# 기하분포
def Ge(ArithmeticErrorp):
x_set = np.arange(1,30)
def f(x):
if x in x_set:
return p * (1-p) ** (x-1) # 확률질량함수 계산
else:
return 0
return x_set, f
p = 0.5
X = Ge(p)
check_prob(X)
plot_prob(X)
plt.show()
# 기하분포 시각화
fig = plt.figure(figsize=(10, 6))
ax = fig.add_subplot(111)
x_set = np.arange(1, 15)
for p, ls in zip([0.2, 0.5, 0.8], linestyles):
rv = stats.geom(p)
ax.plot(x_set, rv.pmf(x_set),
label=f'p:{p}', ls=ls, color='gray')
ax.set_xticks(x_set)
ax.legend()
plt.show()

주어진 함수 의 그래프를 그리고,
그 함수가 특정 구간 에서의 면적을 수치적으로 적분하여 계산
import numpy as np
import matplotlib.pyplot as plt
from scipy import integrate
x_range = np.array([0, 1])
def f(x):
if x_range[0] <= x <= x_range[1]:
return 2 * x
else:
return 0
X = [x_range, f]
xs = np.linspace(x_range[0], x_range[1], 100)
fig = plt.figure(figsize=(10, 6))
ax = fig.add_subplot(111)
ax.plot(xs, [f(x) for x in xs], label='f(x)', color='gray')
ax.hlines(0, -0.2, 1.2, alpha=0.3)
ax.vlines(0, -0.2, 2.2, alpha=0.3)
ax.vlines(xs.max(), 0, 2.2, linestyles=':', color='gray')
# 면적 적분 계산 및 그래프 표시
# 0.4부터 0.6 까지 x좌표를 준비
xs = np.linspace(0.4, 0.6, 100)
# xs의 범위로 f(x)와 x축으로 둘러싸인 영역을 진하게 칠함
ax.fill_between(xs, [f(x) for x in xs], label='prob')
ax.set_xticks(np.arange(-0.2, 1.3, 0.1))
ax.set_xlim(-0.1, 1.1)
ax.set_ylim(-0.2, 2.1)
ax.legend()
plt.show()
# 적분 계산
print(integrate.quad(f, 0.4, 0.6))
from scipy.optimize import minimize_scalar
# y의 확률밀도함수 g(y)
y_range = [3, 5]
def g(y):
if y_range[0] <= y <= y_range[1]:
return (y-3) / 2
# 확률분포함수
def G(y):
return integrate.quad(g, -np.inf, y)[0]
# f 함수의 최소값을 찾기
res = minimize_scalar(f)
print(res.fun)
print(integrate.quad(f, -np.inf, np.inf)[0])
def F(x):
return integrate.quad(f, -np.inf, x)[0]
print(F(0.6) - F(0.4))


모평균에 대한 점추정 + 모분산의 불편추정량
점추정 : 원본 데이터를 사용하여 모집단의 하나의 모수(예: 평균, 분산 등)에 대한 값을 추정
데이터에서 표본을 추출하고, 표본 통계량(평균 등)을 계산하여 모집단의 특성을 추정
-> 표본 평균을 사용하여 모집단의 평균을 추정하는 점추정 예시 + 모분산의 불편 추정량
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
# 데이터 파일 읽기
df = pd.read_csv('C:/Users/campus4D033/ch4_scores400.csv')
# 'score' 열 데이터를 numpy 배열로 변환
scores = np.array(df['score'])
p_mean = np.mean(scores)
p_var = np.var(scores)
fig = plt.figure(figsize=(10, 6))
ax = fig.add_subplot(111)
xs = np.arange(101)
rv = stats.norm(p_mean, np.sqrt(p_var))
ax.plot(xs, rv.pdf(xs), color='gray')
ax.hist(scores, bins=100, range=(0, 100), density=True)
plt.show()
np.random.seed(0)
n = 20 # 모집단에서 뽑을 표본의 개수
sample = np.random.choice(scores, n) # 표본 추출
print(sample)
# 샘플개수 만개로 늘려서 데이터를 만들기 n_sample
# 열이 각 샘플들의 원소들을 갖기
np.random.seed(5)
n_sample = 10000 # 모집단에서 뽑을 표본의 개수
samples = np.random.choice(scores, (n_sample, n)) # 표본 추출
print(samples)
# -------점평균 - 표본평균-------
for i in range(5):
s_mean = np.mean(samples[i])
print(f'{i+1}번째 표본평균: {s_mean:.3f}')
# 표본 평균들의 평균인 점평균(모집단의 평균)을 계산
sample_means = np.mean(samples, axis=1)
print(np.mean(sample_means))
# 모집단에서 100만 개의 데이터를 무작위로 추출하여 그 평균을 계산하고 출력
print(np.mean(np.random.choice(scores, int(1e6))))
s_mean = np.mean(sample)
print(s_mean) # 첫 번째 표본 데이터 sample의 평균
# -------모분산-------
for i in range(5):
s_var = np.var(samples[i])
print(f'{i+1}번째 표본분산: {s_var:.3f}')
sample_vars = np.var(samples, axis=1)
# 표본들의 표본분산의 평균으로, 모집단의 분산에 대한 불편 추정량
print(np.mean(sample_vars))
불편 분산(Unbiased Variance)
: 모집단의 분산을 추정하는 데 사용되는 통계량
모집단의 분산에 대한 신뢰 구간을 계산할 때,
보통 불편 분산을 사용하여 이 구간을 추정
모평균의 점추정 방식
: 모평균을 추정하는 데 사용되는 통계적 추정량이 불편성과 일치성을 만족한다는 의미
즉, 표본 평균이 모집단의 평균을 정확히 추정하며(불편성),
표본의 크기가 충분히 크다면 모집단의 평균에 점점 더 가까워진다는 것(일치성)을 의미
'파이썬 & 머신러닝과 딥러닝' 카테고리의 다른 글
| 데이터베이스 SQL 기본 질의문, 연산자, 함수 및 단일행 함수 (2) | 2024.07.05 |
|---|---|
| 통계기반 데이터 분석 방법, 단순회귀분석, 종회귀모형, 모형의 선택, 모형의 타당성 (1) | 2024.07.03 |
| 상관관계 확인, OpenAPI 사용, beautifulsoup, Selenium, 통계 분석 개념 및 정리 (0) | 2024.07.01 |
| beautifulsoup 기본 및 응용, 토큰화, 정규화, konlpy, wordcloud (0) | 2024.06.28 |
| 파이썬 문법 보충, 데이터 분석 라이브러리 (1) | 2024.06.28 |



