강화학습
- 강화학습은 행동을 선택하여 주어진 환경에서 최대의 보상을 얻기 위해 학습하는 기계 학습
- 에이전트(agent)가 환경(environment)과 상호작용하면서 보상(reward)을 받아, 이를 통해 최적의 정책(policy)을 학습
- 에이전트는 다양한 상태(state)에서 가능한 행동(action)을 선택하고, 그 결과로 보상을 받아 다음 행동을 결정.
밴디트 알고리즘
- 밴디트 문제(Multi-Armed Bandit Problem)는 강화학습의 가장 기본적인 문제 중 하나로, 여러 개의 슬롯 머신(밴디트) 중에서 최적의 슬롯 머신을 선택하는 문제
- 각 슬롯 머신은 서로 다른 확률로 보상을 주며, 에이전트는 한 번의 선택으로 보상을 최대화하기 위해 어떤 슬롯 머신을 선택할지 결정해야 함.
- 에이전트는 탐험(Exploration)과 이용(Exploitation) 사이의 균형을 유지
- 즉, 현재 알고 있는 정보에 기반하여 가장 높은 보상을 제공할 것 같은 슬롯 머신을 선택하면서도, 다른 슬롯 머신을 시도해 볼 기회를 가져야 함.
슬롯 확률 맞추기
# 슬롯 확률 맞추기 // 슬롯마다 확률이 모두 다르다
import numpy as np
game = np.random.rand()
game
1. 게임을 많이 해보는 것: 실험적 확률 추정
rewards = []
for i in range(1, 1001):
if np.random.rand() <= game:
r = 1
else:
r = 0
rewards.append(r)
print(sum(rewards) / i)
목표: 슬롯 게임을 여러 번 시도하여 확률을 직접 계산
반복 횟수가 많아질수록 출력되는 값이 실제 확률(약 0.0273)에 수렴
2. 이전 확률로 현재 확률 추론: 재귀적 업데이트 방식
Q = 0
for n in range(1, 1001):
if np.random.rand() <= game:
r = 1
else:
r = 0
Q = (r - Q) / n + Q
목표: 새로운 데이터를 추가하면서 재귀적인 방식으로 확률을 업데이트

- r은 이번 시도의 결과 (1 또는 0)
- Qn−1은 이전까지의 추정 확률
- 새로운 값을 이전 추정 값에 반영하여 확률을 업데이트
재귀적 업데이트 과정:
- 예를 들어 첫 번째 시도에서 성공하면 Q1=1
- 두 번째 시도에서 실패하면 Q2=1/2(0−1)+1=0.5
- 이런 식으로 점차 모든 시도의 결과를 반영하며 새로운 확률을 계산
지수 이동 평균 (Exponential Moving Average, EMA)
: 이전 값을 이용해 현재 값을 효율적으로 계산

다중 슬롯 머신 문제 시뮬레이션
10개의 슬롯을 가진 게임에서 각각의 슬롯 머신의 성공 확률을 추론
다중 슬롯 머신 문제로, 각 슬롯마다 서로 다른 성공 확률을 가지고 있으며,
여러 번의 시도를 통해 각 슬롯의 성공 확률을 추정
import numpy as np
# 슬롯 머신 게임을 정의하는 클래스
class Game:
def __init__(self, arms=10):
# 슬롯마다 무작위 성공 확률 부여 (0과 1 사이의 값)
self.rates = np.random.rand(arms)
# 특정 슬롯(arm)을 선택해서 플레이
def play(self, arm):
rate = self.rates[arm] # 선택한 슬롯의 성공 확률 가져오기
# 무작위 값이 슬롯의 성공 확률보다 작으면 성공, 그렇지 않으면 실패
if rate > np.random.rand():
return 1 # 성공
else:
return 0 # 실패
# 슬롯 10개의 게임을 생성
game = Game()
# 슬롯 성공 확률을 추정하기 위한 배열 초기화
Qs = np.zeros(10) # 각 슬롯의 추정 성공 확률을 저장하는 배열
Ns = np.zeros(10) # 각 슬롯이 시도된 횟수를 저장하는 배열
# 1000번 슬롯 머신을 플레이
for n in range(1000):
action = np.random.randint(0, 10) # 랜덤하게 10개의 슬롯 중 하나를 선택
r = game.play(action) # 선택한 슬롯을 플레이하여 보상(1 또는 0) 받음
Ns[action] += 1 # 해당 슬롯의 시도 횟수 증가
# 선택한 슬롯의 평균 보상(추정 성공 확률)을 업데이트
Qs[action] += (r - Qs[action]) / Ns[action]
# 1000번의 시도 후 각 슬롯의 추정 성공 확률
print('추정 확률', Qs) # 추정된 성공 확률 출력
# 실제 슬롯의 성공 확률 확인
print('실제 확률', game.rates) # 실제 슬롯 성공 확률 출력
가장 좋은 확률을 가지고 있는 슬롯 선택 (현재 알고 있는 확률 기준)
슬롯 머신 문제에서 가장 높은 보상을 제공할 것으로 예상되는 슬롯을 선택하는 동시에,
일정 확률로 다른 슬롯들도 탐험하여 더 나은 슬롯을 찾을 가능성을 열어둠
→ 탐험(Exploration)과 이용(Exploitation) 전략을 적용한 에이전트(Agent)를 구현
import numpy as np
# 에이전트 클래스: 슬롯 머신 문제에서 가장 좋은 슬롯을 선택하는 역할
class Agent:
def __init__(self, epsilon, action_size=10):
self.epsilon = epsilon # 탐험을 할 확률 (무작위로 슬롯 선택할 확률)
self.Qs = np.zeros(action_size) # 각 슬롯의 보상 추정치(Q값) 저장 배열
self.Ns = np.zeros(action_size) # 각 슬롯이 선택된 횟수 저장 배열
# 보상 업데이트 함수: 선택한 슬롯(action)의 보상(reward)으로 Q값 업데이트
def update(self, action, reward):
self.Ns[action] += 1 # 선택된 슬롯의 횟수 증가
# 선택된 슬롯의 Q값(보상 추정치) 업데이트 (재귀적 평균 업데이트 방식)
self.Qs[action] += (reward - self.Qs[action]) / self.Ns[action]
# 행동 선택 함수: epsilon-탐욕 정책에 따라 슬롯 선택
def get_action(self):
# 무작위로 행동할 확률(epsilon)에 따라 랜덤 선택(탐험)
if np.random.rand() < self.epsilon:
return np.random.randint(0, len(self.Qs)) # 무작위 슬롯 선택
# 그렇지 않으면 현재 Q값(보상 추정치)이 가장 높은 슬롯 선택(이용)
else:
return np.argmax(self.Qs) # Q값이 가장 높은 슬롯 선택
# 슬롯 머신 게임 클래스
class Game:
def __init__(self, arms=10):
# 10개의 슬롯에 각각 무작위 성공 확률 설정
self.rates = np.random.rand(arms)
# 특정 슬롯을 플레이하고 성공(1) 또는 실패(0) 결과 반환
def play(self, arm):
rate = self.rates[arm] # 선택한 슬롯의 성공 확률
# 무작위 값이 성공 확률보다 작으면 성공(1), 그렇지 않으면 실패(0)
if rate > np.random.rand():
return 1
else:
return 0
# 슬롯 10개의 게임 생성
game = Game()
# ε-탐욕 정책을 따르는 에이전트 생성 (탐험 확률 epsilon=0.1)
agent = Agent(epsilon=0.1)
# 1000번의 슬롯 머신 플레이
for n in range(1000):
action = agent.get_action() # 에이전트가 슬롯 선택
reward = game.play(action) # 선택된 슬롯 플레이 후 보상 얻음
agent.update(action, reward) # 선택된 슬롯의 보상으로 Q값 업데이트
# 1000번의 시도 후 각 슬롯의 추정된 보상(Q값)
print(agent.Qs)
# 실제 슬롯의 성공 확률 확인
print(game.rates)
동작 방식
- 탐험(Exploration): 10% 확률로(즉, epsilon=0.1) 무작위로 슬롯을 선택하여 더 나은 슬롯을 탐색
- 이용(Exploitation): 90% 확률로 현재까지 가장 보상이 높다고 추정되는 슬롯을 선택
- 매번 슬롯을 선택한 후, 선택한 슬롯의 보상 추정치를 보상을 기반으로 업데이트하여 점점 더 정확한 추정
→ ε-탐욕 알고리즘을 적용하여, 보상이 높은 슬롯을 선택하는 동시에 다른 슬롯도 탐험하는 전략을 구현
→ 10개의 슬롯에서 매번 게임을 할 때마다 에이전트가 어떤 슬롯을 선택할지 결정하고, 그 결과로 보상 확률을 추정
# 스텝 수와 epsilon 설정
steps = 1000 # 게임을 진행할 총 스텝 수
epsilon = 0.1 # 무작위 행동을 선택할 확률
# 슬롯 머신 게임 인스턴스 생성
game = Game()
# ε-탐욕 정책을 따르는 에이전트 인스턴스 생성
agent = Agent(epsilon)
# 총 보상 초기화
total_reward = 0
# 각 스텝에서의 총 보상을 저장할 리스트
total_rewards = []
# 평균 보상을 저장할 리스트
rates = []
# 각 스텝에서 슬롯 머신 플레이
for step in range(steps):
action = agent.get_action() # 에이전트가 슬롯 선택
reward = game.play(action) # 선택된 슬롯을 플레이하여 보상 얻음
agent.update(action, reward) # 선택된 슬롯의 보상으로 Q값 업데이트
total_reward += reward # 총 보상에 현재 보상 추가
total_rewards.append(total_reward) # 총 보상 리스트에 추가
# 현재까지의 평균 보상 계산 (현재 총 보상을 스텝 수로 나누어 평균 계산)
rates.append(total_reward / (step + 1)) # 평균 보상 리스트에 추가total_reward

import matplotlib.pyplot as plt
plt.plot(total_rewards)
plt.grid()
plt.show()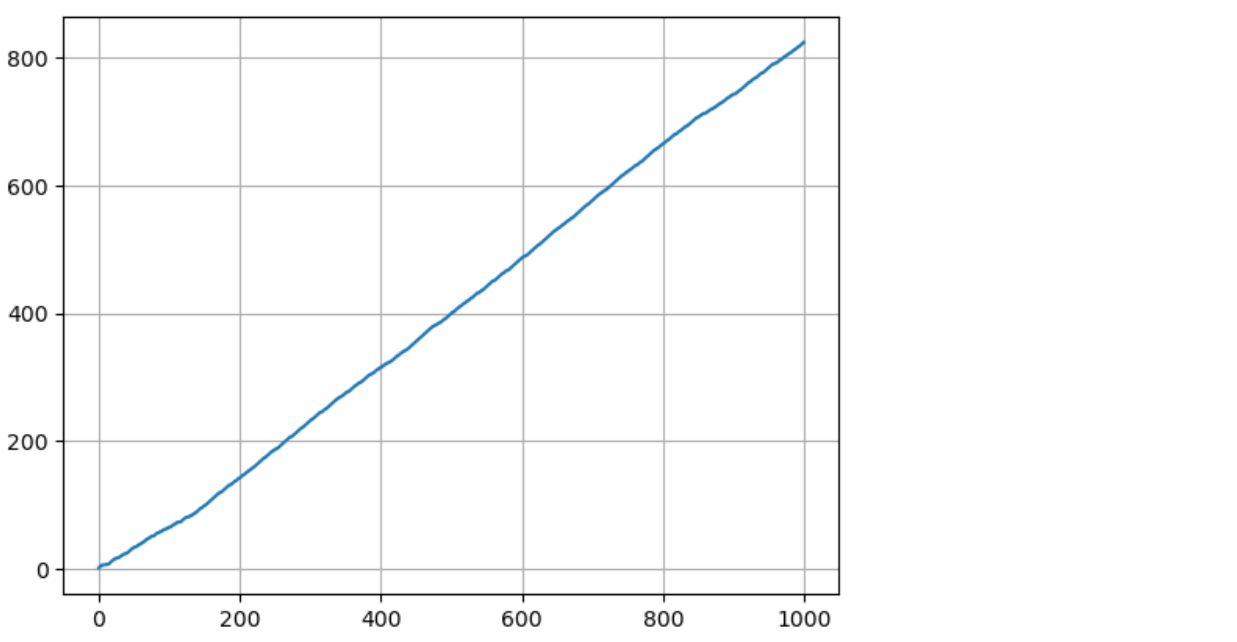
plt.plot(rates)
plt.grid()
plt.show()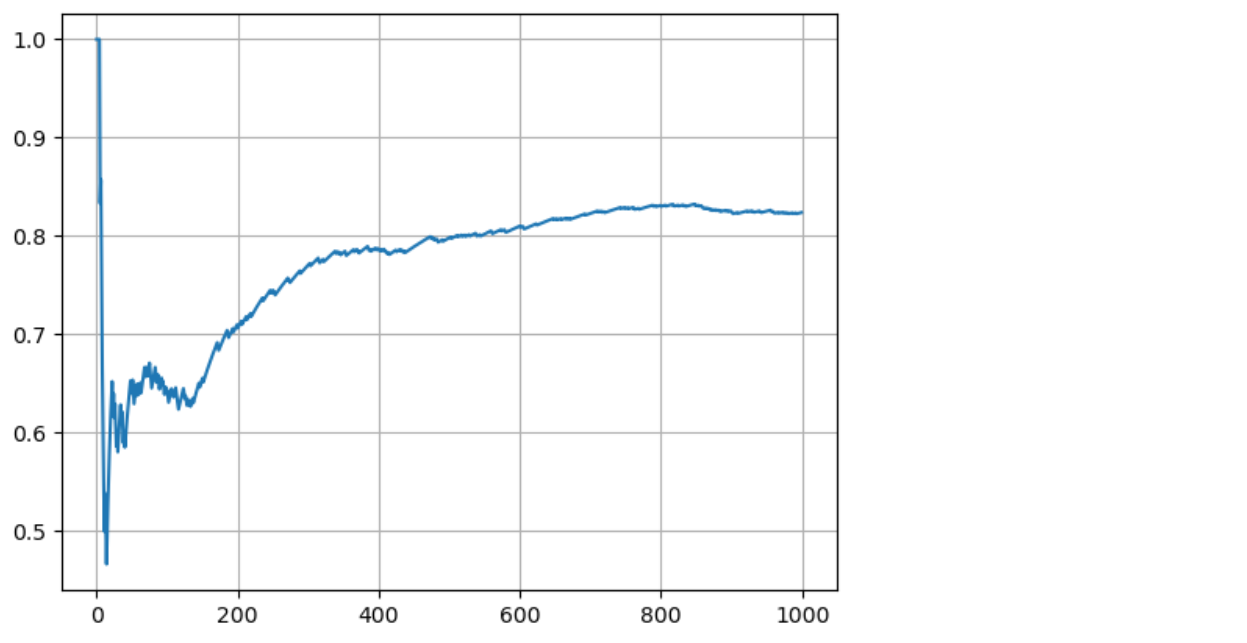
밴딧 알고리즘 구현
ε-탐욕 정책을 이용한 슬롯 머신 강화학습 시뮬레이션
→ 다양한 슬롯 머신에서 에이전트가 보상을 최대화하도록 학습하는 과정.
# 실험을 수행할 총 횟수 설정
runs = 200 # 총 200번의 실행(run)
# 각 실행에서의 평균 보상을 저장할 2D 배열 초기화
all_rates = np.zeros((runs, steps)) # (실행 횟수, 각 실행에서의 스텝 수) 크기의 배열 생성
# 각 실행(run)마다 반복
for run in range(runs):
game = Game() # 새로운 슬롯 머신 게임 인스턴스 생성
agent = Agent(epsilon) # ε-탐욕 정책을 따르는 새로운 에이전트 인스턴스 생성
total_reward = 0 # 현재 실행에서의 총 보상 초기화
rates = [] # 현재 실행에서의 평균 보상을 저장할 리스트 초기화
# 각 실행의 스텝 수만큼 반복
for step in range(steps):
action = agent.get_action() # 에이전트가 슬롯 머신 중 하나를 선택
reward = game.play(action) # 선택된 슬롯을 플레이하여 보상 얻음
agent.update(action, reward) # 받은 보상으로 선택한 슬롯의 Q값 업데이트
total_reward += reward # 현재 보상(total_reward)에 보상 추가
# 현재까지의 평균 보상을 계산하여 리스트에 추가
rates.append(total_reward / (step + 1)) # 현재 총 보상을 (step + 1)로 나누어 평균 계산하여 rates에 추가
# 현재 실행(run)의 평균 보상을 all_rates 배열에 저장
all_rates[run] = rates # 각 실행의 평균 보상을 all_rates 배열에 저장→ 현재 실행(run)에서의 평균 보상 결과를 all_rates 배열에 저장
avg_rates = all_rates.mean(axis = 0)
plt.plot(avg_rates)
plt.grid()
plt.show()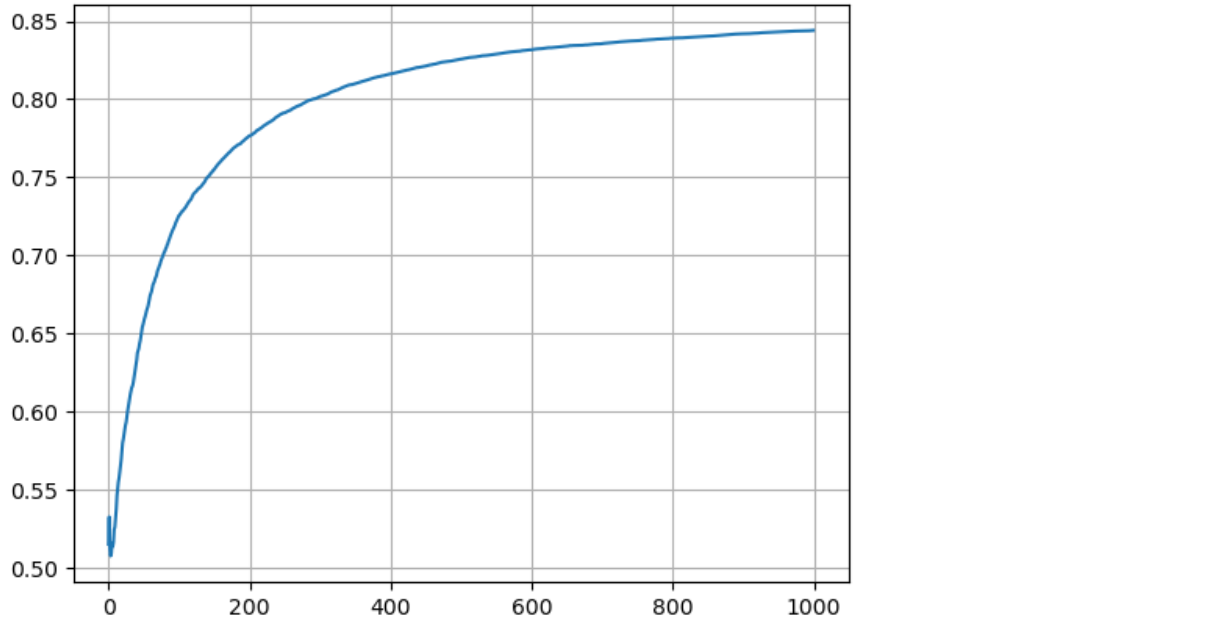
무작위로 행동할 확률을 0.01, 0.1, 0.3으로 설정한 후에 비교
import numpy as np
import matplotlib.pyplot as plt
# epsilon 값을 0.01, 0.1, 0.3으로 설정하여 비교
for e in [0.01, 0.1, 0.3]:
runs = 200 # 각 epsilon에 대해 반복할 실행 횟수
all_rates = np.zeros((runs, steps)) # 각 실행에서의 보상을 저장할 배열 초기화
# 여러 번의 실행을 통해 평균 보상을 계산
for run in range(runs):
game = Game() # 새로운 게임 인스턴스 생성
agent = Agent(e) # 현재 epsilon 값으로 에이전트 생성
total_reward = 0 # 총 보상 초기화
rates = [] # 각 단계에서의 평균 보상을 저장할 리스트 초기화
# 각 단계에서 에이전트의 행동 수행
for step in range(steps):
action = agent.get_action() # 현재 에이전트의 행동 선택
reward = game.play(action) # 선택한 행동에 대한 보상 받기
agent.update(action, reward) # 에이전트 업데이트
total_reward += reward # 총 보상 업데이트
rates.append(total_reward / (step + 1)) # 현재까지의 평균 보상 저장
all_rates[run] = rates # 현재 실행의 보상 저장
avg_rates = all_rates.mean(axis=0) # 모든 실행에 대한 평균 보상 계산
plt.plot(avg_rates, label=str(e)) # 평균 보상을 그래프에 추가
plt.grid() # 그리드 추가
plt.legend() # 범례 추가
plt.show() # 그래프 표시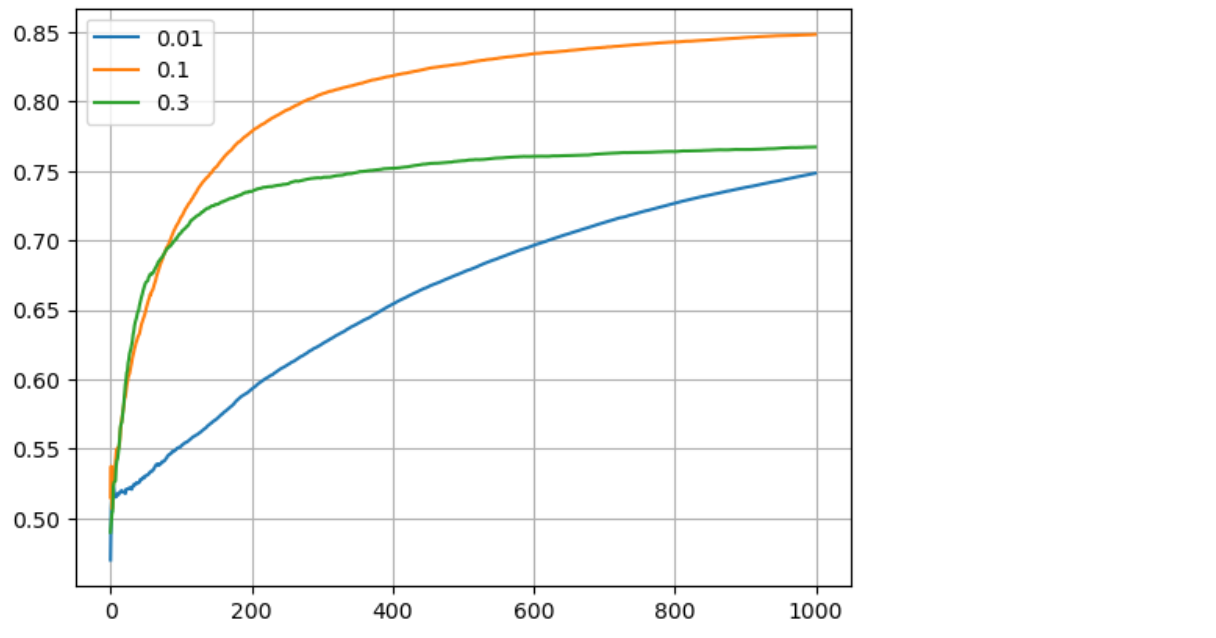
* 매번 슬롯들의 확률을 조금씩 변형한다면?
Q-러닝 알고리즘의 업데이트 규칙
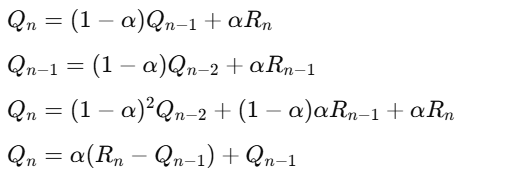

현재 보상 Rn과 이전 추정 Qn−1을 사용하여 Q값을 업데이트하는 방식
import numpy as np # NumPy 라이브러리 임포트
import matplotlib.pyplot as plt # Matplotlib 라이브러리 임포트
# 게임 환경을 정의하는 클래스
class Game2:
def __init__(self, arms=10):
self.arms = arms # 슬롯 머신의 팔 수
self.rates = np.random.rand(arms) # 각 팔의 성공 확률을 랜덤으로 초기화
def play(self, arm):
rate = self.rates[arm] # 선택한 팔의 성공 확률
self.rates += 0.1 * np.random.randn(self.arms) # 각 팔의 성공 확률에 노이즈 추가
# 랜덤 값이 팔의 성공 확률보다 작으면 보상 1, 아니면 0 반환
return 1 if rate > np.random.rand() else 0
# 에이전트의 동작을 정의하는 클래스
class Agent2:
def __init__(self, epsilon, alpha, action_size=10):
self.epsilon = epsilon # 무작위 행동 선택 확률
self.Qs = np.zeros(action_size) # 각 팔에 대한 Q-값 초기화
self.alpha = alpha # 학습률 (알파)
def update(self, action, reward):
# Q-값 업데이트 공식을 사용하여 Qs[action] 업데이트
self.Qs[action] += (reward - self.Qs[action]) * self.alpha # 보상과 Q-값의 차이를 기반으로 업데이트
def get_action(self):
# 탐험(exploration)과 착취(exploitation) 선택
if np.random.rand() <= self.epsilon: # 무작위 행동 선택
return np.random.randint(0, len(self.Qs)) # 0부터 Qs 길이까지 랜덤하게 선택
else: # 현재 Q-값을 기반으로 최적의 팔 선택
return np.argmax(self.Qs) # Q-값이 가장 큰 팔을 선택
# 실행 및 실험 설정
runs = 200 # 에이전트 테스트 실행 횟수
steps = 1000 # 각 실행에서의 스텝 수
epsilon = 0.1 # 무작위 행동 선택 확률
alpha = 0.8 # 학습률
types = ['sample average', "alpha const update"] # 비교할 에이전트 유형
results = {} # 결과를 저장할 딕셔너리 초기화
# 각 에이전트 유형에 대해 반복
for agent_type in types:
all_rates = np.zeros((runs, steps)) # 모든 실행에 대한 보상률을 저장할 배열 초기화
for run in range(runs): # 각 실행에 대해 반복
# 에이전트 유형에 따라 에이전트 인스턴스 생성
if agent_type == "sample average":
agent = Agent(epsilon) # 샘플 평균을 사용하는 에이전트
else:
agent = Agent2(epsilon, alpha) # 알파 고정 업데이트를 사용하는 에이전트
game = Game2() # 게임 인스턴스 생성
total_reward = 0 # 총 보상을 초기화
rates = [] # 각 스텝의 평균 보상을 저장할 리스트 초기화
# 각 스텝에 대해 반복
for step in range(steps):
action = agent.get_action() # 에이전트의 행동 선택
reward = game.play(action) # 선택한 행동으로부터 보상 받기
agent.update(action, reward) # 에이전트의 Q값 업데이트
total_reward += reward # 총 보상 누적
rates.append(total_reward / (step + 1)) # 현재까지의 평균 보상 계산
all_rates[run] = rates # 각 실행의 보상률 저장
avg_rates = np.mean(all_rates, axis=0) # 모든 실행에 대한 평균 보상률 계산
results[agent_type] = avg_rates # 결과 딕셔너리에 평균 보상률 저장
# 평균 보상률을 그래프로 시각화
for key, avg_rates in results.items():
plt.plot(avg_rates, label=key) # 각 에이전트의 평균 보상률 그래프에 추가
plt.grid() # 그리드 추가
plt.legend() # 범례 표시
plt.show() # 그래프 보여주기
- Game2 클래스:
- 슬롯 머신의 팔을 모델링하며, 각 팔의 성공 확률은 랜덤으로 초기화
- play 메서드는 선택된 팔에 대해 보상을 계산하고 노이즈를 추가하여 실제 성공 확률을 변화시킴.
- Agent2 클래스:
- 에이전트의 행동을 결정하는 데 필요한 변수와 메서드를 포함
- update 메서드는 선택한 팔의 보상을 기반으로 Q-값을 업데이트. 학습률 alpha를 사용하여 업데이트의 크기를 조절.
- get_action 메서드는 ε-greedy 정책을 사용하여 무작위 행동과 최적의 팔 선택을 결정
- 실험 설정:
- 총 200번의 실행(run) 동안 1000스텝(step)씩 반복하여 각 에이전트의 성능을 평가
- "샘플 평균"과 "알파 고정 업데이트" 두 가지 에이전트의 성능을 비교
밴디드 알고리즘을 사용해서 KOSPI 상승장 종목 찾기
Q-값 설명
- Q-값이란?
- Q-값은 특정 상태(state)에서 특정 행동(action)을 선택했을 때 기대되는 누적 보상의 추정값 (가)
- Q-learning 알고리즘에서는 주어진 상태와 행동에 대한 Q-값을 업데이트하면서 최적의 정책(policy)을 학습
- 특정 슬롯 머신(또는 행동)에서 기대할 수 있는 보상의 평균 값
- Q-값이 0.9보다 크다는 것
- if Q > 0.9: 조건문은 Q-값이 특정 기준 이상일 때만 상승 보상을 계산하고, 보상률을 업데이트하겠다는 의미
- Q-값이 0.9보다 크다는 것은 해당 행동이 기대되는 보상이 상당히 높다는 것을 의미
- 즉, 행동이 과거에 비해 긍정적인 결과를 많이 가져왔다는 것과 해당 행동을 반복할 가능성이 높아진 것을 나타냄.
# 필요한 라이브러리 임포트
import os # 운영 체제와 상호작용을 위한 라이브러리
import pandas as pd # 데이터 조작과 분석을 위한 라이브러리
import FinanceDataReader as fdr # 금융 데이터 수집을 위한 라이브러리
# 초기 변수 설정
total_reward = 0 # 총 보상 초기화
alpha = 0.8 # 학습률 설정
count = 0 # 상승 보상의 수
rates = [] # 보상률 저장 리스트 초기화
# KOSPI 상장 종목 목록 가져오기
kospi = fdr.StockListing('KOSPI') # KOSPI 상장 종목 데이터를 가져옴
kospi.head() # 상위 5개 종목 표시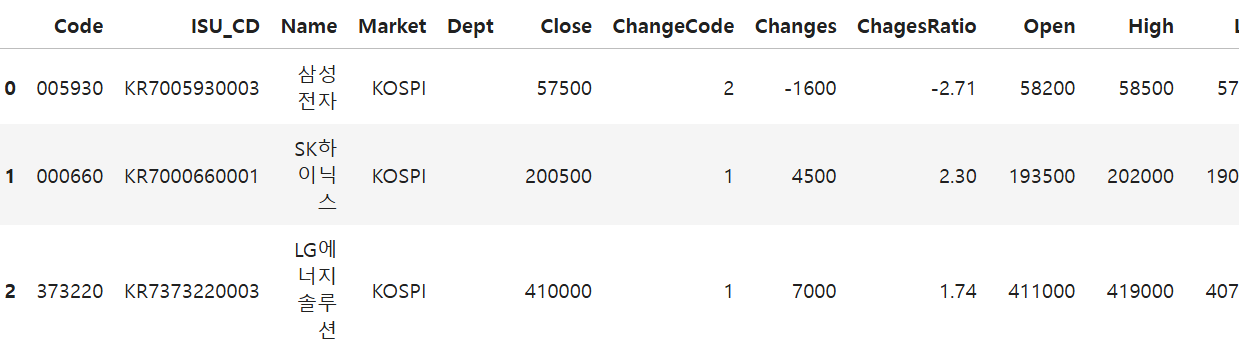
from tqdm import tqdm # 진행 상황을 시각적으로 보여주는 라이브러리
# 주요 변수 재설정
alpha = 0.8 # 학습률
rates = [] # 보상률 저장 리스트 초기화
count = 0 # 상승 보상의 수 초기화
total_count = 0 # 총 시도 횟수 초기화
box = [] # 최종 결과를 저장할 리스트 초기화
# KOSPI 상장 종목 수 만큼 반복
for i in tqdm(range(len(kospi))):
a = kospi.iloc[i] # 현재 종목의 정보 가져오기
code = a['Code'] # 종목 코드
name = a['Name'] # 종목 이름
df = fdr.DataReader(code) # 해당 종목의 주가 데이터 가져오기
Q = 0 # Q-값 초기화 (현재 주식의 가치 평가)
# 해당 종목의 주가 데이터에 대해 반복
for j in range(len(df) - 1):
# 오늘 종가가 내일 종가보다 5% 이상 상승했는지 확인
if df.iloc[j]['Close'] * 1.05 < df.iloc[j + 1]['Close']:
reward = 1 # 상승했으면 보상 1
else:
reward = 0 # 상승하지 않았으면 보상 0
# Q-값이 특정 기준을 넘었을 때만 보상률 계산
if Q > 0.9:
total_count += 1 # 총 시도 횟수 증가
if reward == 1:
count += 1 # 상승 보상이 발생했으면 카운트 증가
rates.append(count / total_count) # 보상률 계산하여 저장
# Q-값 업데이트: 현재 보상과 Q-값의 차이를 alpha로 가중하여 Q-값에 반영
Q = Q + (reward - Q) * alpha
# 최종 결과를 박스에 저장: 종목 이름과 Q-값
box.append([name, Q])df = pd.DataFrame(box, columns = ['종목', 'Q'])
df = df.sort_values('Q', ascending = False)
df[df['Q'] > 0.9]
KOSPI 상장 종목의 상승 가능성을 강화 학습을 통해 평가하는 과정
1. 각 종목의 주가 데이터에 대해 다시 반복하여 오늘의 종가가 내일의 종가보다 5% 이상 상승했는지를 확인
→ 조건이 충족되면 reward를 1로 설정하고, 그렇지 않으면 0으로 설정
2. Q-값이 0.9보다 클 때만 보상률을 계산.
→ 상승 보상이 발생한 경우 count를 증가시키고, 총 시도 횟수에 대해 보상률을 계산하여 rates에 저장.
→ 이후, Q-값은 현재 보상과 기존 Q-값의 차이를 반영하여 업데이트
3. 마지막으로, 각 종목의 이름과 해당 종목의 Q-값을 리스트 box에 저장
→ 나중에 상승 가능성이 높은 종목을 평가하는 데 사용
'파이썬 & 머신러닝과 딥러닝' 카테고리의 다른 글
| 뉴스기사 & 리뷰 (텍스트 데이터) 주가 예측 (3) | 2024.10.30 |
|---|---|
| RSI, 볼린저 밴드를 활용한 투자 전략 (EMA, finterstellar 라이브러리 사용) (3) | 2024.10.29 |
| 변동성 돌파 전략, 마켓 타이밍 전략 (4) | 2024.10.23 |
| 주식 포트폴리오 분석을 위한 시뮬레이션 - 몬테카를로 시뮬레이션, 샤프지수, KOSPI 통계분석, 종목간 상관관계, 최대 낙폭, 할로윈 투자 전략 (2) | 2024.10.21 |
| 금융 데이터 전처리 (주식 데이터월별, 분기별, 주별 데이터 집계, 거래량 변화 탐지, 모멘텀 전략 및 수익률 계산, 볼린저 밴드) (2) | 2024.10.21 |



