주식 포트폴리오 분석을 위한 시뮬레이션
주식 포트폴리오의 수익률과 위험도를 계산하는 과정
이를 기반으로 몬테카를로 시뮬레이션을 통해 다양한 비율로 포트폴리오를 구성하여 수익률과 위험도를 분석
몬테카를로 시뮬레이션:
- 다양한 주식 비중으로 포트폴리오를 구성하고, 그에 따른 예상 수익률과 위험도를 계산
- 무작위로 비중을 선택하여, 각 포트폴리오가 얼마나 수익을 낼 수 있는지 평가
- 10,000번 반복하여 다양한 포트폴리오를 테스트
pct_change() 함수 : 각 주식의 일간 퍼센트 변동률을 계산
cov() 함수 : 공분산 행렬을 계산하여, 각 주식 간의 변동성을 평가하는 데 사용
1. 데이터 불러오기 및 전처리
'stocks.csv' 파일에서 날짜와 주식 종목 데이터를 불러와서 일간 수익률을 계산하는 기반을 마련
import pandas as pd
import numpy as np
# 1. 데이터 불러오기
df = pd.read_csv('stocks.csv')
# 2. 'Unnamed: 0' 컬럼을 날짜 데이터로 변환하고, 이를 인덱스로 설정
df['Unnamed: 0'] = pd.to_datetime(df['Unnamed: 0'])
df = df.set_index('Unnamed: 0')
# 데이터 확인
df.head() # 상위 5개 행 출력
2. 일간 및 연간 수익률 계산
일간 수익률은 주식의 퍼센트 변동률을 계산하여 얻음.
이를 평균내어 1년(252 거래일 기준) 동안의 예상 수익률을 계산
# 3. 일간 수익률 계산 (각 주식의 일간 퍼센트 변화율)
daily_ret = df.pct_change()
# 4. 연간 수익률 계산 (일간 수익률의 평균에 252를 곱하여 연간 수익률로 변환)
annual_ret = daily_ret.mean() * 252
# 연간 수익률 확인
print("연간 수익률:\n", annual_ret)
3. 분산(위험도) 및 변동성 계산
일간 수익률의 공분산을 계산하여 일간 위험도를 구하고, 이를 바탕으로 연간 위험도를 계산
이 위험도는 주식의 변동성을 나타냄
# 5. 일간 위험도(분산) 계산
daily_cov = daily_ret.cov()
# 6. 연간 위험도 계산 (일간 공분산을 252로 곱해 연간 위험도로 변환)
annual_cov = daily_cov * 252
# 연간 위험도 확인
print("연간 위험도(공분산):\n", annual_cov)
4. 몬테카를로 시뮬레이션
이제 다양한 비율로 주식 포트폴리오를 구성하여, 각 포트폴리오의 수익률과 위험도를 계산
이를 10,000번 반복해서 다양한 포트폴리오의 성과를 시뮬레이션
import numpy as np
box = []
stocks = ['TSLA', 'AAPL', 'NVDA']
# 몬테카를로 시뮬레이션
# 자산의 비중(weights)을 랜덤하게 설정한 후, 이를 바탕으로 포트폴리오의 수익률과 리스크를 계산
for i in range(10000):
# 자산의 랜덤 비중(weights) 생성 (각 자산에 대한 비율)
weights = np.random.random(len(stocks)) # 주어진 자산(stocks) 개수만큼 임의의 가중치 생성
weights /= sum(weights) # 가중치의 합이 1(즉, 100%)이 되도록 정규화
# 포트폴리오의 예상 수익률 계산
# 각 자산의 연간 수익률(annual_ret)과 자산의 비중(weights)을 내적(dot product)하여 포트폴리오의 수익률 계산
returns = np.dot(weights, annual_ret)
# 포트폴리오의 예상 리스크(변동성) 계산
# 가중치(weights)와 연간 공분산 행렬(annual_cov)을 사용하여 리스크 계산
risk = np.sqrt(np.dot(weights.T, np.dot(annual_cov, weights)))
# 수익률(returns), 리스크(risk), 자산별 가중치(weights)를 box 리스트에 추가
# [수익률, 리스크] + [각 자산의 가중치] 형식으로 저장
box.append([returns, risk] + list(weights))df = pd.DataFrame(box, columns = ['Returns', 'Risk'] + stocks)
df
import matplotlib.pyplot as plt
df.plot.scatter(x = 'Risk', y = 'Returns', figsize = (10, 5), grid = True)
plt.xlabel('Risk')
plt.ylabel('Returns')
plt.show()
같은 리스크라도 Returns 가 높은걸 구매하는게 좋다
→ 샤프 비율 사용
샤프 지수(Sharpe Ratio)
투자 성과를 평가하기 위한 지표로, 위험 대비 수익률을 측정
샤프 지수 : (수익률 - 무위험수익률) / 위험도
(은행보단 수익이 더 나와야해서 무위험수익률을 뺌)
샤프 지수를 포함한 몬테카를로 시뮬레이션
import numpy as np
box = []
stocks = ['TSLA', 'AAPL', 'NVDA']
# 몬테카를로 시뮬레이션
# 자산의 구매 비중에 따라 포트폴리오 수익률, 리스크, 샤프지수를 계산
# 샤프지수: (포트폴리오 수익률 - 무위험 수익률) / 포트폴리오 리스크
for i in range(10000):
# 자산의 랜덤 비중(weights) 생성
weights = np.random.random(len(stocks)) # 주어진 자산(stocks) 개수만큼 임의의 가중치 생성
weights /= sum(weights) # 가중치의 합이 1(100%)이 되도록 정규화
# 포트폴리오의 예상 수익률 계산
returns = np.dot(weights, annual_ret)
# 포트폴리오의 예상 리스크(변동성) 계산
risk = np.sqrt(np.dot(weights.T, np.dot(annual_cov, weights)))
# 샤프 지수 계산
# 무위험 수익률을 사용하여 샤프 지수를 계산 (여기서는 무위험 수익률을 0으로 가정)
sharpe = returns / risk # 샤프 지수 = (포트폴리오 수익률) / (포트폴리오 리스크)
# box 리스트에 수익률, 리스크, 샤프 지수, 자산별 비중 추가
# [수익률, 리스크, 샤프 지수] + [각 자산의 가중치] 형식으로 저장
box.append([returns, risk, sharpe] + list(weights))
# [수익률, 리스크, 샤프지수] + [각 자산의 가중치] 형식으로 저장
df = pd.DataFrame(box, columns = ['Returns', 'Risk', 'Sharpe'] + stocks)
df
# 최대 샤프 지수의 포트폴리오 정보 찾기
max_sharpe = df[df['Sharpe'] == df['Sharpe'].max()] # 샤프 지수가 가장 높은 포트폴리오 정보
max_sharpe
# 최소 리스크의 포트폴리오 정보 찾기
min_risk = df[df['Risk'] == df['Risk'].min()] # 리스크가 가장 낮은 포트폴리오 정보
min_risk # 가장 안전한 포트폴리오 정보
import matplotlib.pyplot as plt
# 리스크(Risk)와 수익률(Returns)을 산점도로 시각화
df.plot.scatter(x='Risk', y='Returns', c='Sharpe', cmap='viridis',
edgecolor='k', figsize=(10, 5), grid=True)
# 최대 샤프 지수 포트폴리오를 빨간 별표로 표시
plt.scatter(x=max_sharpe['Risk'], y=max_sharpe['Returns'],
c='r', marker='*', s=300, label='Max Sharpe')
# 최소 리스크 포트폴리오를 빨간 X로 표시
plt.scatter(x=min_risk['Risk'], y=min_risk['Returns'],
c='r', marker='X', s=300, label='Min Risk')
# x축 및 y축 레이블 추가
plt.xlabel('Risk') # 리스크 레이블
plt.ylabel('Returns') # 수익률 레이블
# 범례 추가
plt.legend()
# 시각화 출력
plt.show()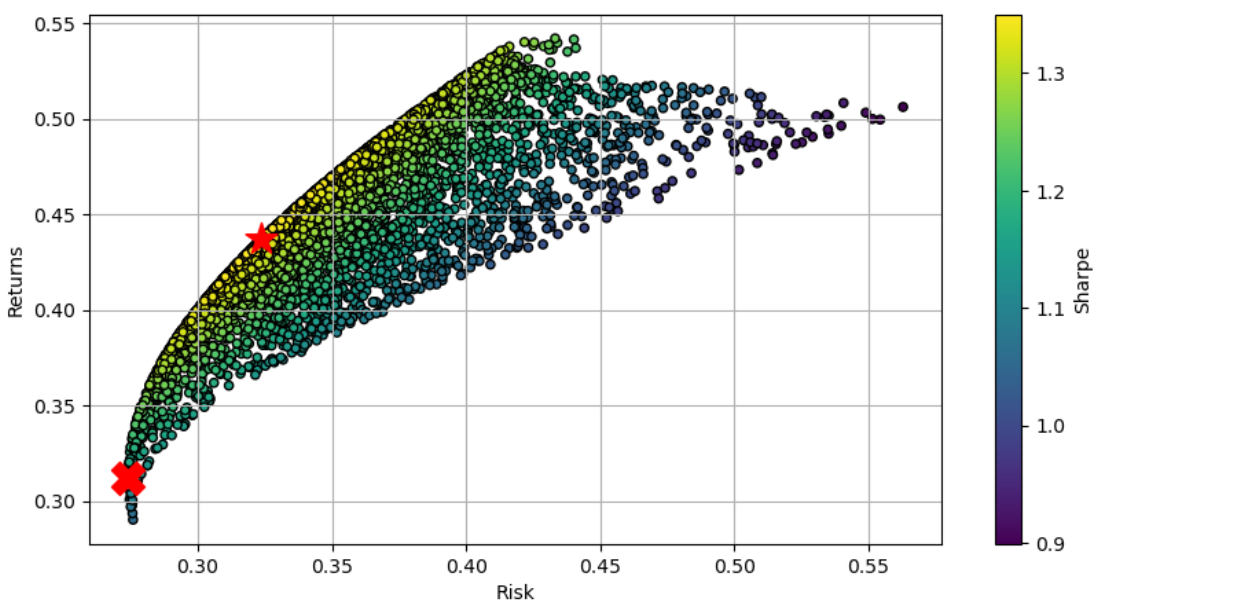
→ 최대 샤프 지수 포트폴리오를 빨간 별표로 최소 리스크 포트폴리오를 빨간 X로 표시
종목간 상관관계
import pandas as pd
import matplotlib.pyplot as plt
import FinanceDataReader as fdr
# 1. 데이터 로드 및 전처리
df = pd.read_excel('20210914.xlsx', index_col=0)[['종목명', '종가', '시가총액']] # Excel 파일에서 종목명, 종가, 시가총액 열을 로드하고 첫 번째 열을 인덱스로 사용
df['비중'] = df['시가총액'] / df['시가총액'].sum() * 100 # 각 종목의 시가총액 비중 계산
df.sort_values('비중', ascending=False) # 비중 기준으로 데이터프레임을 내림차순 정렬
# KOSPI와 삼성전자의 관계를 분석하기 위한 주석
# KOSPI = 삼성전자?
# 2. KOSPI 및 삼성전자 주가 데이터 가져오기
kospi = fdr.DataReader('KOSPI') # KOSPI 지수 데이터를 가져옴
samsung = fdr.DataReader('005930') # 삼성전자 주가 데이터를 가져옴
# 3. KOSPI와 삼성전자의 종가 데이터 결합
data = [kospi['Close'], samsung['Close']] # KOSPI와 삼성전자의 종가 데이터를 리스트로 만듦
df = pd.concat(data, axis=1, keys=['kospi', 'samsung']).dropna() # 데이터를 데이터프레임으로 결합하고 결측치 제거
# 4. KOSPI와 삼성전자의 산점도 그리기
df.plot.scatter(x='samsung', y='kospi') # 삼성전자의 종가를 x축, KOSPI 종가를 y축으로 산점도 그리기
plt.title('Samsung vs KOSPI Scatter Plot') # 산점도 제목 추가
plt.xlabel('Samsung Price') # x축 레이블 추가
plt.ylabel('KOSPI Price') # y축 레이블 추가
plt.grid() # 그리드 추가
plt.show() # 산점도 그래프 출력
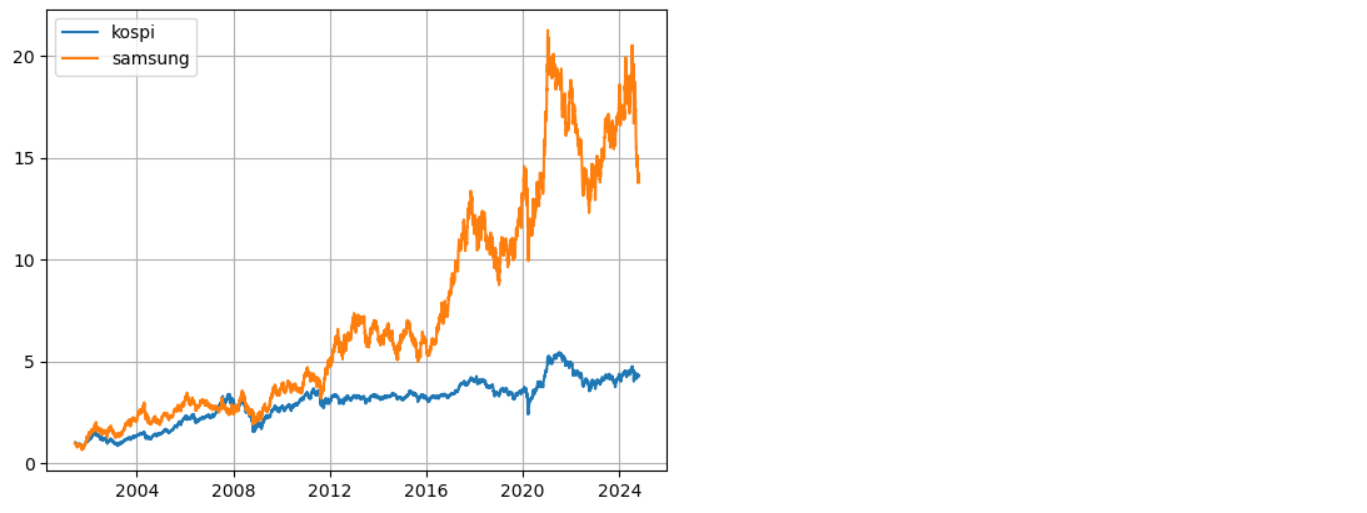
# 5. KOSPI와 삼성전자 주가의 비율 계산
A = df['kospi'] / df['kospi'].iloc[0] # KOSPI 주가의 비율 계산 (첫 날 주가 기준)
B = df['samsung'] / df['samsung'].iloc[0] # 삼성전자 주가의 비율 계산 (첫 날 주가 기준)
# 6. KOSPI와 삼성전자의 비율 시각화
plt.plot(A) # KOSPI 비율 그래프
plt.plot(B) # 삼성전자 비율 그래프
plt.legend(['KOSPI', 'Samsung']) # 범례 추가
plt.grid() # 그리드 추가
plt.title('Price Ratio Over Time') # 비율 그래프 제목 추가
plt.xlabel('Days') # x축 레이블 추가
plt.ylabel('Price Ratio') # y축 레이블 추가
plt.show() # 비율 그래프 출력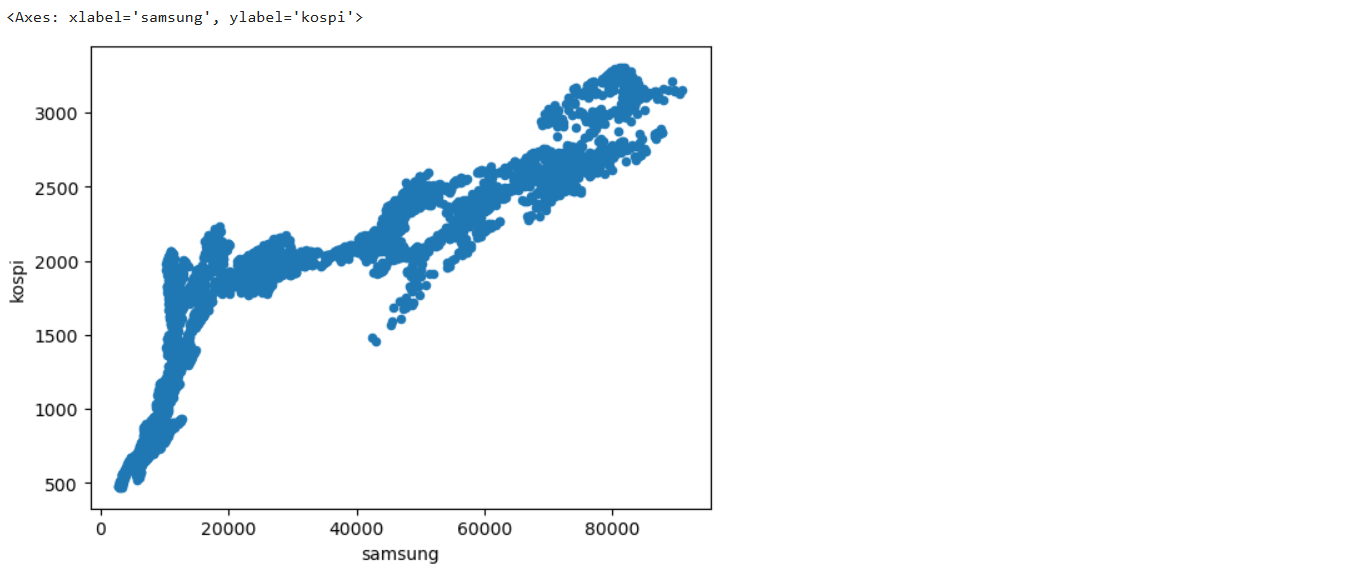
KOSPI 종목 중 SK하이닉스와 가장 상관관계가 높은 종목과 낮은 종목을 찾아보기
import os # 운영 체제와 상호작용하기 위한 모듈
import pandas as pd # 데이터 처리 및 분석을 위한 pandas 라이브러리
box = [] # 상관계수를 저장할 리스트 초기화
# SK하이닉스 주식 데이터 불러오기
sk = pd.read_csv("KOSPI/SK하이닉스.csv") # CSV 파일에서 SK하이닉스 주식 데이터 읽기
sk['Date'] = pd.to_datetime(sk['Date']) # 'Date' 컬럼을 datetime 형식으로 변환
sk = sk.set_index("Date") # 'Date' 컬럼을 인덱스로 설정
sk = sk['Close'] # 'Close' 컬럼만 선택하여 변수 sk에 저장
# KOSPI 폴더 내의 모든 파일에 대해 반복
for i in os.listdir("KOSPI"): # KOSPI 폴더 내 파일 리스트 가져오기
name = i.split('.')[0] # 파일명에서 확장자를 제거하여 주식명 저장
df = pd.read_csv("KOSPI/" + i) # CSV 파일에서 현재 주식 데이터 읽기
df['Date'] = pd.to_datetime(df['Date']) # 'Date' 컬럼을 datetime 형식으로 변환
df = df.set_index("Date") # 'Date' 컬럼을 인덱스로 설정
df = df['Close'] # 'Close' 컬럼만 선택하여 변수 df에 저장
# SK하이닉스와 현재 주식 데이터를 열 방향으로 결합
a = pd.concat([sk, df], axis=1, keys=['A', 'B'])
# 두 데이터프레임의 상관계수 계산 (절대값)
corr = abs(a.corr().iloc[0, 1])
# 상관계수와 주식명 리스트에 추가
box.append([name, corr])
# 상관계수를 데이터프레임으로 변환하고 Corr 컬럼 기준으로 정렬
result = pd.DataFrame(box, columns=['Name', 'Corr']).sort_values('Corr')
# 상관계수가 가장 낮은 주식 정보 출력
print(result.iloc[0])
print() # 빈 줄 출력
# 상관계수가 두 번째로 높은 주식 정보 출력
print(result.iloc[-2])
KOSPI(한국 종합주가지수)에 대한 다양한 통계 분석
import FinanceDataReader as fdr
import pandas as pd
# KOSPI 데이터 가져오기
kospi = fdr.DataReader('KOSPI')
# KOSPI 데이터 확인
print(kospi)
# KOSPI 종가의 최대값과 최소값 출력
max_close = kospi['Close'].max() # 최대 종가
min_close = kospi['Close'].min() # 최소 종가
print(max_close, min_close)
# 최대 종가의 날짜 찾기
date_max = kospi['Close'].idxmax() # 최대 종가가 발생한 날짜
print(date_max)
# 최소 종가의 날짜 찾기
date_min = kospi['Close'].idxmin() # 최소 종가가 발생한 날짜
print(date_min)
# 변동폭 계산 (현재 종가 - 이전 종가)
kospi['변동폭'] = kospi['Close'] - kospi['Close'].shift(1)
# 변동폭이 가장 큰 5일 데이터 정렬 후 상위 5개 출력
top_5_volatility = kospi.sort_values('변동폭', ascending=False).head(5)
print(top_5_volatility)
# 변동폭이 가장 작은 5일 데이터 출력
smallest_5_volatility = kospi['변동폭'].nsmallest(5)
print(smallest_5_volatility)
# KOSPI 데이터를 리셋하여 새로운 DataFrame 생성
kospi2 = kospi.reset_index()
print(kospi2.head())
# KOSPI 월별 정리 - 각 월의 첫 시가, 마지막 종가, 최고가, 최저가, 거래량 총합 계산
how = {
'Open': 'first', # 월의 첫 거래일 시가
'Close': 'last', # 월의 마지막 거래일 종가
'High': 'max', # 월의 최고가
'Low': 'min', # 월의 최저가
'Volume': 'sum' # 월의 거래량 총합
}
monthly_summary = kospi2.groupby(pd.Grouper(key='Date', freq='MS')).agg(how) # 월별 그룹화 및 집계 수행
print(monthly_summary)
# KOSPI 지수가 100 포인트를 달성했을 때의 날짜와 지수 찾기
box = []
for i in range(400, 3400, 100): # 400 포인트부터 3400 포인트까지 100 단위로 반복
cond = kospi['Close'] >= i # 현재 지수가 i 이상인 조건
if not cond.empty: # 조건이 존재할 경우
box.append([f'{i} 포인트 돌파!', # 이벤트 메시지
kospi.index[cond][0], # 해당 포인트를 처음 달성한 날짜
kospi.loc[cond, 'Close'].iloc[0]]) # 해당 날짜의 지수
# 이벤트 결과를 DataFrame으로 변환하여 출력
event_summary = pd.DataFrame(box, columns=['이벤트', '일자', '지수'])
print(event_summary)

KOSPI 지수에서 "포인트" : KOSPI 지수의 수준
KOSPI 지수는 주식 시장의 전체적인 상태를 나타내는 수치로, 보통 포인트라는 단위로 표시
예를 들어, KOSPI 지수가 2400포인트라면 KOSPI의 지수 값이 2400을 의미하는 것이고,
이 값이 상승하거나 하락할 때마다 그 변동을 포인트 단위로 표현
KOSPI 기간 수익률
: KOSPI 지수의 처음과 마지막 종가를 비교하여 기간 동안 얼마나 상승했는지 백분율로 계산
rate = kospi.iloc[-1, 3] / kospi.iloc[0, 3] # 마지막 행의 4번째 열(종가) / 첫 번째 행의 4번째 열(종가)
rate = (rate - 1) * 100 # 기간 수익률을 백분율로 변환
rate
연 복리 수익률 (CAGR)
: 특정 기간 동안의 평균 연간 성장률을 측정하는 지표
diff = kospi.index[-1] - kospi.index[0] # 기간 계산 (마지막 날짜 - 첫 번째 날짜)
year = diff.days / 365 # 기간을 연도로 환산
cagr = rate ** (1/year) - 1 # 연 복리 수익률 계산
cagr


최대 낙폭(MDD)
삼성전자(종목 코드: 005930)의 최대 낙폭(MDD, Maximum Drawdown)을 계산하고 시각화
최대 낙폭(MDD)이란?
- 낙폭(Drawdown)은 특정 시점에서 주가가 이전 최고점에서 얼마나 하락했는지를 백분율로 나타냄.
- 최대 낙폭(MDD)은 투자 기간 중 가장 큰 낙폭을 의미(리스크를 평가하는 중요한 지표)
kospi = fdr.DataReader('005930') # 삼성전자 데이터를 불러옴
kospi['전고점'] = kospi['Close'].cummax() # 누적된 고점을 계산
# 낙폭 계산
kospi['DD'] = (1 - kospi['Close'] / kospi['전고점']) * 100 # 낙폭을 백분율로 계산
(1 - kospi['Close'] / kospi['전고점']) * 100: 주가가 전고점 대비 몇 퍼센트 하락했는지 계산
MDD = kospi['DD'].max() # 낙폭 중 가장 큰 낙폭 (최대 낙폭)
MDD
fig = plt.figure(figsize = (15, 5))
ax1 = fig.add_subplot(2, 1, 1)
ax2 = fig.add_subplot(2, 1, 2)
# 주가와 낙폭을 각각 그리기
ax1.plot(kospi.index, kospi['Close'], label = 'Close') # 주가(종가) 그래프
ax2.plot(kospi.index, kospi['DD'] * -1, label = 'Drawdown') # 낙폭 그래프 (음수로 그려짐)
ax2.fill_between(kospi.index, kospi['DD'] * -1, alpha = 0.5) # 낙폭 영역을 음영 처리
# 그리드와 범례 추가
ax1.grid()
ax2.grid()
ax1.legend()
ax2.legend()
# 그래프 표시
plt.show()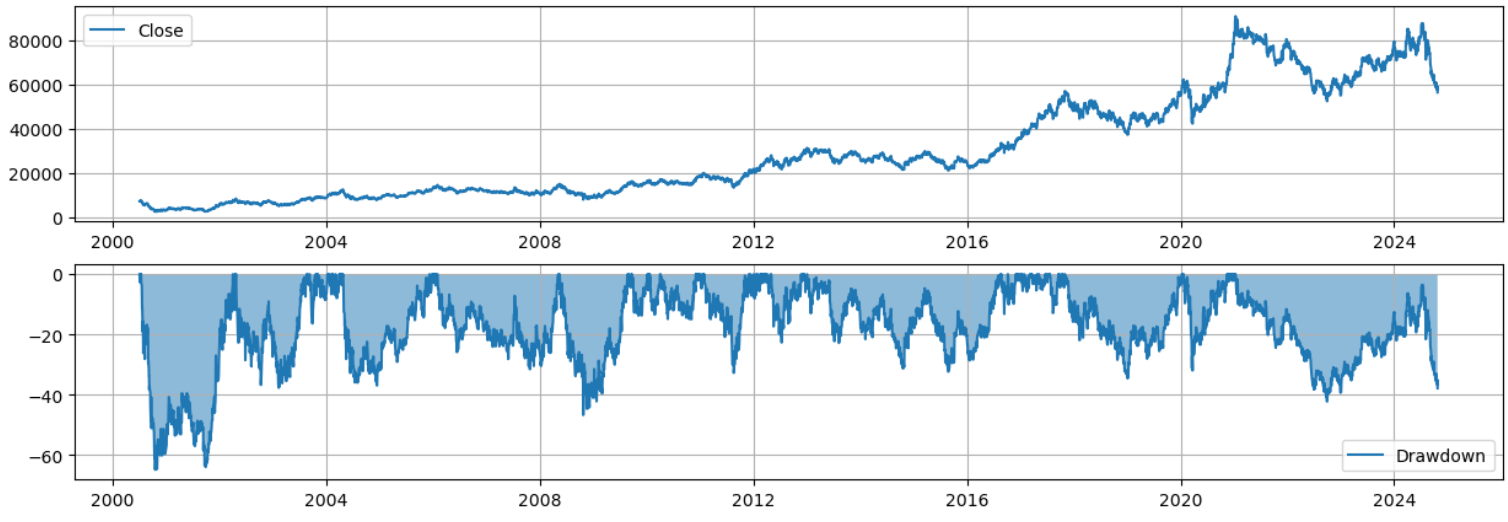
할로윈 투자 전략
: 11월에 매수하고 다음 해 4월에 매도하는 전략
할로윈 투자 전략을 백테스팅하는 과정과 매월 투자했을 경우의 누적 수익률을 계산하는 과정
1. 누적 수익률 계산
2001년부터 2023년까지 매년 11월에 매수하고 다음 해 4월에 매도하는 전략으로 누적 수익률을 계산
# 할로윈 투자 전략 백테스팅 (2001 ~ 2023년) : 11월에 매수하고 다음 해 4월에 매도하는 전략
cum_rate = 1 # 누적 수익률을 1로 초기화
for year in range(2001, 2024): # 2001년부터 2023년까지 반복
buy_mon = str(year) + '-11' # 매수 시점: 해당 연도의 11월
sell_mon = str(year + 1) + '-04' # 매도 시점: 다음 연도의 4월
buy_price = kospi.loc[buy_mon].iloc[0]['Open'] # 해당 11월의 첫 번째 영업일의 시가 매수
sell_price = kospi.loc[sell_mon].iloc[-1]['Close'] # 해당 4월의 마지막 영업일의 종가 매도
rate = sell_price / buy_price # 해당 기간의 수익률 계산
cum_rate = cum_rate * rate # 누적 수익률 계산
# 최종 누적 수익률 출력
cum_rate # 약 18배의 누적 수익률
→ 누적 수익률 약 18배
2. 연평균 수익률(CAGR) 계산
# 연평균 수익률(CAGR) 계산 (연 복리 수익률)
CAGR = (cum_rate ** (1/24)) - 1 # 24년 기간 동안의 연평균 수익률 계산
CAGR # 연평균 수익률 출력
→ 24년 기간 동안 매년 발생한 평균적인 수익률 12배
3. 단순 보유 시 수익률 비교
# 단순 보유했을 때의 누적 수익률 계산
simple_rate = kospi.iloc[-1]['Close'] / kospi.iloc[0]['Open'] # 처음부터 끝까지 단순히 주식을 보유했을 때의 누적 수익률
simple_rate # 약 8배
→ 같은 기간 동안 주식을 단순히 보유했을 경우의 누적 수익률은 약 8배
# 단순 보유 시의 연평균 수익률 계산
simple_rate ** (1/24) - 1 # 24년간 단순 보유했을 때의 연평균 수익률
# 연평균 수익률 약 9%
3. 정말로 11월에 사면 좋은지?
# 정말로 11월에 사는 것이 더 좋은지 확인하기 위해 각 달에 매수했을 경우 비교
import datetime
from dateutil.relativedelta import relativedelta
# 시작 날짜를 2001년 11월 1일로 설정
start = datetime.datetime(year = 2001, month = 11, day = 1)
# 시작 날짜로부터 5개월 후인 4월로 설정
end = start + relativedelta(month = 5)
start.strftime('%Y - %m') # 날짜 형식 출력# 6개월 주기로 매수, 매도하는 수익률을 계산하는 함수
def month6(df, start_year=2001, end_year=2021, month=11):
cum_rate = 1 # 누적 수익률 초기화
for year in range(start_year, end_year+1): # 주어진 기간 동안 매년 반복
start = datetime.datetime(year=year, month=month, day=1) # 매수 시작 시점
end = start + relativedelta(months=5) # 매도 시점은 매수 시점으로부터 5개월 후
buy_mon = start.strftime("%Y-%m") # 매수 시점(연도-월)
sell_mon = end.strftime("%Y-%m") # 매도 시점(연도-월)
# 매수 시점의 첫 번째 영업일 시가
buy_price = df.loc[buy_mon].iloc[0]['Open']
# 매도 시점의 마지막 영업일 종가
sell_price = df.loc[sell_mon].iloc[-1]['Close']
rate = sell_price / buy_price # 해당 기간 수익률 계산
cum_rate = cum_rate * rate # 누적 수익률 계산
return cum_rate # 최종 누적 수익률 반환# 매달 투자했을 때의 누적 수익률을 계산하는 코드
data = {}
for month in range(1, 13): # 1월부터 12월까지 모든 달에 대해 반복
ret = month6(kospi, 2001, 2021, month) # 각 달에 매수했을 경우의 누적 수익률 계산
print(month, ret) # 해당 달의 수익률 출력
data[month] = ret # 결과를 딕셔너리에 저장
# 11월에 투자했을 때의 수익률 계산
month6(kospi, 2001, 2023, 11)
# 월별 누적 수익률을 시각화 (막대 그래프 그리기)
plt.bar(data.keys(), data.values()) # 월별로 수익률을 막대로 표현
plt.xlabel('Month') # x축 라벨: Month (월)
plt.ylabel('Return') # y축 라벨: Return (수익률)
plt.xticks([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]) # x축 값 설정 (1월~12월)
plt.grid(axis='y') # y축에 그리드 추가
plt.show() # 그래프 출력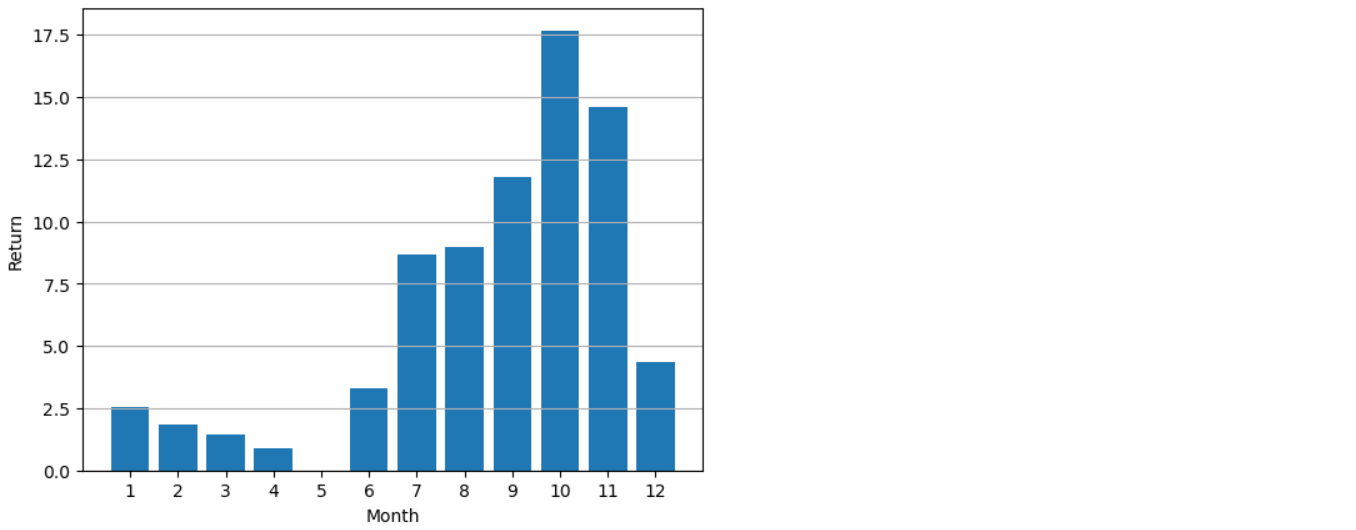
'파이썬 & 머신러닝과 딥러닝' 카테고리의 다른 글
| 강화학습 - 밴디트 알고리즘(슬롯 확률 시뮬레이션, 상승장 종목 찾기) (2) | 2024.10.24 |
|---|---|
| 변동성 돌파 전략, 마켓 타이밍 전략 (4) | 2024.10.23 |
| 금융 데이터 전처리 (주식 데이터월별, 분기별, 주별 데이터 집계, 거래량 변화 탐지, 모멘텀 전략 및 수익률 계산, 볼린저 밴드) (1) | 2024.10.21 |
| Okt 형태소 분석기(빈도기반), 워드클라우드, 상대빈도분석(오즈비 분석), TF-IDF 분석 (1) | 2024.10.14 |
| 자연어 처리(NLP) - 감성분석, OpenAI (6) | 2024.10.11 |



