비율 검정
모집단의 비율에 대한 가설을 검정하는 통계적 방법
특정 비율이 주어진 값과 같은지 또는 두 비율이 동일한지 여부를 확인하는 데 사용
비율검정은 주로 이항 분포를 기반으로 하며,
여기서 성공 또는 실패와 같은 두 가지 가능한 결과만 있는 경우에 적용
1. 단일 비율 검정 (One-Proportion Z-Test)
- 목적: 단일 모집단 비율이 특정 값과 다른지 확인 -> 한 집단의 비율이 특정 비율과 같은지 비교
- 가설 수립:
- 귀무 가설 (H0): 모집단 비율 p는 특정 값 p0와 같다.
- 대립 가설 (H1): 모집단 비율 p는 특정 값 p0와 다르다 (양측 검정).
- 검정 통계량:
- 검정 통계량 Z는 다음과 같이 계산

- 해석:
- 계산된 Z 값과 표준 정규 분포를 사용하여 p 값을 구함
- p 값이 유의수준 (예: 0.05)보다 작으면 귀무 가설을 기각
2. 두 비율 검정 (Two-Proportion Z-Test)
- 목적: 두 모집단의 비율이 동일한지 확인 -> 두 집단간 비율 비교
- 가설 수립:
- 귀무 가설 (H0): 두 모집단의 비율 p1과 p2는 같다.
- 대립 가설 (H1): 두 모집단의 비율 p1과 p2는 다르다 (양측 검정).
- 검정 통계량:
- 검정 통계량 Z는 다음과 같이 계산됨

- 해석:
- 계산된 Z 값과 표준 정규 분포를 사용하여 p 값을 구함
- p 값이 유의수준 (예: 0.05)보다 작으면 귀무 가설을 기각합
비율검정_연습
1. 1 Proportion Test
고급강 A제품을 가공하는 국내 고객사는 전체 중에 10% 정도가 품질만족을 나타내고 있다.
한 해 동안 A제품의 품질개선의 노력을 통하여 전체고객 중 100여개의 업체를 표본으로하여
가공품질을 확인한 결과, 15개의 업체가 품질만족을 나타냈다.
그러면 기존보다 품질만족의 비율에 차이가 있는가? (유의수준 0.05)
# 1 Proportion Test
count = 15
n_obs = 100
value = 0.1
# Proportion Test 실행
z, p = proportions_ztest(count, n_obs, value)
# Proportion 결과 출력
print('1 Proportion Test')
print('z: {0:0.3f}'.format(z))
print('p: {0:0.3f}'.format(p))
-> 결과적으로 고급강 A제품에 대해 품질개선 결과 기존 대비 사용비율이 차이가 있다고 할 수 없다
1-2. 동전이 정상적인지 검정하기 위해 100번 던져본 결과, 앞면 40번, 뒷면 60번 나왔다.
이 동전이 정상인지를 유의수준 0.05로써 검정
정상적인 동전을 던질 때, 앞면이 나올 확률을 50% 이다 (귀무가설)
# 1 Proportion Test
count = 40 # 앞면 횟수
n_obs = 100 # 총횟수
value = 0.5 # 귀무가설 비율
# Proportion Test 실행
z, p = proportions_ztest(count, n_obs, value)
# Proportion 결과 출력
print('1 Proportion Test')
print('z: {0:0.3f}'.format(z))
print('p: {0:0.3f}'.format(p))
-> z-score가 -2.041이라는 것은
관찰된 비율이 귀무가설에서 기대하는 비율 (0.5)에서 표준편차의 약 2.041배 만큼 낮게 위치한다는 의미
-> 유의수준 0.05보다 작으면 귀무가설을 기각하게 되어, 이 경우에는 동전이 정상적이지 않다
2-1. 동일한 제품을 생선하는 두 공장에서 불량품을 측정한 결과가 아래와 같다
두 공정의 불량률이 같다고 할 수 있는가? (유의수준 0.05)
- 공장A : N1 = 1000, X1 = 4
- 공장B : N2 = 1200, X2 = 1
귀무가설 : 불량률 같다
대립가설 : 불량률 다르다
import numpy as np
# 2 Proportion Test
count = np.array([4, 1])
nobs = np.array([1000, 1200])
# Proportion test 실행
z, p = proportions_ztest(count, nobs)
# Proportion test 결과 출력
print("2 Proportion test")
print('z : {0:0.3f}'.format(z))
print('p:{0:0.3f}'.format(p))
-> 결론 : P-value > 0.05이므로 두 공장의 불량률은 차이가 있다고 할 수 있다.
2-2. 동일한 제품을 생선하는 두 공장에서 불량품을 측정한 결과가 아래와 같다
두 공정의 불량률이 같다고 할 수 있는가? (유의수준 0.05)
- 공장A : N1 = 1200, X1 = 14
- 공장B : N2 = 1200, X2 = 5
import numpy as np
# 2 Proportion Test
count = np.array([14, 5])
nobs = np.array([1200, 1200])
# Proportion test 실행
z, p = proportions_ztest(count, nobs)
# Proportion test 결과 출력
print("2 Proportion test")
print('z : {0:0.3f}'.format(z))
print('p:{0:0.3f}'.format(p))
-> p-value가 0.05보다 작기 때문에 대립가설 채택
불량률이 같다고 할 수 없다
분산 검정
두 개의 분산이 동일한지 확인하는 방법
각각의 집단 간의 분산 비교를 통해, 주어진 가설이 옳은지 검정합니다.
2-Variances F-test
2-Variances F-test는 두 집단 간의 분산이 동일한지 비교하는 데 사용
이는 두 집단의 분산 비율이 1인지 검정
F-검정은 다음 가정을 따른다
- 두 표본은 독립적입니다.
- 각 표본은 정규 분포를 따릅니다.
F-검정의 절차:
- 가설 수립:
- 귀무가설(H0): 두 집단의 분산이 동일하다.
- 대립가설(H1): 두 집단의 분산이 동일하지 않다.
- F-통계량 계산

- 자유도 계산:
- 분자 자유도(dfn) = n1−1
- 분모 자유도(dfd) = n2−1
- p-값 계산:
- p값은 F-분포를 사용하여 계산
import numpy as np
from scipy.stats import f
# 두 집단의 데이터 예시
group1 = [10, 12, 14, 15, 17, 18, 19]
group2 = [22, 24, 26, 27, 29, 30, 32]
# 각 집단의 분산 계산
var1 = np.var(group1, ddof=1)
var2 = np.var(group2, ddof=1)
# F-통계량 계산
f_stat = var1 / var2
# 자유도 계산
dfn = len(group1) - 1
dfd = len(group2) - 1
# p-값 계산
p_value = 1 - f.cdf(f_stat, dfn, dfd)
print(f'F-statistic: {f_stat}, p-value: {p_value}')
Equal Variance Test
Equal Variance Test는 Levene's Test와 같은 방법을 포함하여
두 개 이상의 집단 간의 분산이 동일한지 여부를 검정
Levene's Test는 데이터가 정규 분포를 따르지 않더라도 사용할 수 있다.
-> 3 집단간의 분산 비교
Levene's Test 절차:
- 가설 수립:
- 귀무가설(H0): 두 집단의 분산이 동일하다.
- 대립가설(H1): 두 집단의 분산이 동일하지 않다.
- 검정 통계량 계산:
- Levene's Test는 각 관측값에서 각 그룹의 중앙값을 뺀 절대값을 사용하여 변형된 ANOVA를 수행합니다.
- p-값 계산:
- ANOVA를 통해 얻은 통계량을 사용하여 p-값을 계산
import scipy.stats as stats
# 여러 집단의 데이터 예시
group1 = [10, 12, 14, 15, 17, 18, 19]
group2 = [22, 24, 26, 27, 29, 30, 32]
group3 = [32, 34, 36, 37, 39, 40, 42]
# Levene's Test 수행
stat, p_value = stats.levene(group1, group2, group3)
print(f'Levene’s Test statistic: {stat}, p-value: {p_value}')
요약
- 2-Variances F-test는 두 집단의 분산이 동일한지 여부를 확인하는 데 사용. -> 주로 정규 분포를 가정.
- Equal Variance Test는 여러 집단의 분산이 동일한지 여부를 확인하는 데 사용
- Levene's Test와 같은 방법은 데이터가 정규 분포를 따르지 않더라도 사용할 수 있다.
카이제곱검정
범주형 데이터 간의 관계를 분석하는 통계적 방법으로, 주로 세 가지 목적으로 사용됨
: 동일성 검정, 독립성 검정, 적합도 검정
1. 동일성 검정 (Test of Homogeneity)
목적: 두 개 이상의 독립된 모집단이 동일한 범주형 변수의 분포를 가지고 있는지를 검정
예시: 여러 공장에서 제조한 제품의 결함율이 동일한지 비교할 때 사용할 수 있다.
절차:
- 각 모집단에서 표본을 추출하여 범주형 데이터를 관찰
- 관측된 빈도와 기대 빈도 사이의 차이를 비교하여 검정 통계량을 계산
- 검정 통계량에 대해 카이제곱 분포를 사용하여 유의확률(p-value)을 계산
- 유의수준에 따라 검정 결과를 해석
2. 독립성 검정 (Test of Independence)
목적: 두 범주형 변수 간의 관계가 독립적인지 여부를 검정
예시: 성별과 흡연 여부 간의 관계를 검정하여 성별에 따라 흡연 여부가 다른지를 알아볼 때 사용할 수 있다.
절차:
- 관측된 빈도와 기대 빈도 사이의 차이를 비교하여 검정 통계량을 계산
- 검정 통계량에 대해 카이제곱 분포를 사용하여 유의확률(p-value)을 계산
- 유의수준에 따라 검정 결과를 해석
3. 적합도 검정 (Goodness of Fit Test)
목적: 관측된 데이터가 특정 이론적 분포와 일치하는지 여부를 검정
예시: 주사위를 던졌을 때 나오는 눈의 수가 고르게 나오는지 검정할 때 사용할 수 있다.
절차:
- 관측된 빈도와 기대 빈도 사이의 차이를 비교하여 검정 통계량을 계산
- 검정 통계량에 대해 카이제곱 분포를 사용하여 유의확률(p-value)을 계산
- 유의수준에 따라 검정 결과를 해석
주요 포인트:
- 검정 통계량 계산: 관측된 빈도와 기대 빈도 사이의 차이를 통해 계산됨.
- 유의확률(p-value): 검정 통계량을 기반으로 하여 귀무가설을 기각할지 말지를 결정하는데 사용. 작은 p-value는 귀무가설을 기각할 증거
- 자유도(df)
자유도 : 모집단에서 얻은 표본 데이터로부터 계산된 통계량이 자유롭게 변동할 수 있는 정도
카이제곱검정에서 자유도는 ( 범주의 수 - 1 )
검정에 사용되는 표본의 수와 관련이 있으며,
독립성 검정과 적합도 검정에서는 (행의수-1)*(열의수-1)의 자유도가 사용됨
행과 열의 수가 증가하면 자유도는 증가하게 되며, 이는 χ² 분포에서의 카이제곱 통계량의 크기를 작게 만든다.
카이제곱 검정통계량이 작다는 것은 실측치와 기대치 차이가 작아 귀무가설을 채택하게 됨
-> 귀무가설 차이 없다고 나올 수 있고 차이 보고싶은 열만 가져와서 돌려야함
카이제곱 검정통계량이 크가는 것은 실측치 대비 기대치의 크기가 크다는 것을 의미함으로 귀무가설을 기각
즉, 자유도가 증가할수록 검정의 정확성과 신뢰도가 증가하는 경향이 있다
표준편차를 모르는 경우에는 표본의 크기에 따라서 자유도가 결정된다.
일반적으로 표준편차를 모르는 상황에서는 t-분포를 사용하여 추론을 수행하게 되는데,
이때의 자유도는 다음과 같이 결정된다.
표준편차를 모르는 상황에서 표본의 표준편차(s)를 사용하여 t-통계량을 계산하는 경우,
자유도는 표본 크기(n)에서 1을 뺀 값이 됩니다. 즉, 자유도 df=n−1 (여기서 n은 표본의 크기)
이 자유도는 t-분포의 모양을 결정하며, 표본의 크기가 클수록 t-분포는 표준 정규분포에 가까워지게 됨.
따라서, 표본의 크기가 클수록 t-분포의 꼬리가 더 얇아지고, 통계적 추론에서의 신뢰도가 증가다.
카이제곱_연습
chi : 얻은 검정통계량, dof : 자유도 expected : 기대치
1. 근무조별로 철강제품을 생산하고 있는데, 생산 제품의 규격이 3가지 종류가 있다.
근무조별로 제품을 생산하는 부하는 차이가 있는가? (유의수준 0.05)
귀무가설 : 차이가 없다
대립가설 : 차이가 있다
# chi-square
df = pd.DataFrame({'Work_1' : [270, 228, 277], 'Work_2':[260, 285, 284],
'Work_3' : [236, 225, 231], 'Work_4':[234, 262, 208]})
# chi-square 검정
chi, pval, dof, expected = stats.chi2_contingency(df)
# chi-square test 결과 출력
print('chi_square test')
print('chisq: {0:0.3f}'.format(chi))
print('p: {0:0.3f}'.format(pval))
print('degree pf freedom: {}'.format(dof))
print('expected value: \n{}'.format(expected.round(3)))
-> p < 0.05 이므로 대립가설 채택
유의수준 5%에서 근무조별로 제품을 생성하는데 부하 차이가 있다고 할 수 있다.
1-2. 노트북 컴퓨터의 6가지 제품(A,B,C,D,E,F)에 대하여 7가지 제품의 이미지를 중복선택 할 수 있도록
32명의 소비자를 대상으로 설문조사한 테이블이다.
각 제품에 대해 이미지에 대해 차이가 있겠는가? (유의수준 0.05)
귀무가설 : 차이가 없다
대립가설 : 차이가 있다
# chi-square
df = pd.DataFrame({'A' : [18,1,8,7,10,9,10],'B' : [8,2,14,5,5,9,4], 'C' : [4,1,3,4,9,5,4],
'D' : [4,1,2,3,2,7,3], 'E' : [3,1,3,1,1,1,1], 'F' : [3,25,8,10,2,1,7]})
# chi-square 검정
chi, pval, dof, expected = stats.chi2_contingency(df)
# chi-square test 결과 출력
print(' chi-square test ')
print('chisq: {0:0.3f}'.format(chi))
print('p: {0:0.3f}'.format(pval))
print('degree pf freedom : {}'.format(dof))
print('expected value: \n{}'.format(expected.round(3)))
-> p < 0.05 이므로 대립가설 채택
차이가 1개 이상 있다
ANOVA (분산분석, Analysis of Variance)
ANOVA는 데이터를 그룹 별로 분류하고,
그룹 간의 변동과 그룹 내의 변동을 비교하여
통계적으로 유의미한 차이가 있는지를 판단
일반적으로 ANOVA는 다음과 같은 가정 하에 진행:
- 독립성: 각 그룹의 데이터는 독립적이다.
- 정규성: 각 그룹의 데이터는 정규분포를 따라야 함
- 등분산성: 각 그룹의 데이터는 분산이 동일하다.
ANOVA의 종류
- 일원배치분산분석(One-Way ANOVA):
- 하나의 요인(독립 변수)을 가진 실험에서 그룹 간 평균 차이를 분석
- 예를 들어, 서로 다른 교육 방법을 적용한 그룹의 성적 비교.
- 이원배치분산분석(Two-Way ANOVA):
- 두 개의 요인(독립 변수)을 가진 실험에서 그룹 간 평균 차이를 분석
- 예를 들어, 서로 다른 교육 방법과 성별에 따른 성적 비교.
ANOVA의 계산 방법
ANOVA는 다음과 같은 세 가지 변동 요소를 계산하여 진행됩니다:
- 총 변동(Total Variation):
- 전체 데이터의 변동을 나타내며, 각 데이터 포인트와 전체 평균 간의 차이의 제곱의 합으로 계산
- 군간 변동(Between-Group Variation):
- 각 그룹의 평균과 전체 평균 간의 차이를 제곱하여, 그룹 간의 변동을 나타냄
- 군간 변동이 클수록 그룹 간 평균 차이가 크다는 것을 의미
- 그룹 내 변동(Within-Group Variation):
- 각 그룹 내 데이터 포인트와 해당 그룹의 평균 간의 차이의 제곱의 합으로, 그룹 내의 무작위 변동을 나타냄냄
ANOVA 검정 통계량
ANOVA에서는 군간 변동과 그룹 내 변동의 비율인 F-비를 사용하여 검정. F-비는 다음과 같이 계산:
F = 군간 변동의 평균 제곱 / 군내 변동(그룹 내 변동)의 평균 제곱 = SSF(Factor) / SSE(Error)
ANOVA의 결과 해석
ANOVA의 결과는 F-비와 그에 따른 p-value를 통해 해석:
- F-비: 군간 변동과 그룹 내 변동의 비율을 나타내며, 클수록 그룹 간 평균 차이가 크다는 것을 의미.
- p-value: 귀무 가설(모든 그룹의 평균이 동일하다는 가설)을 기각할 수 있는 유의성 수준. 작을수록 그룹 간의 평균 차이가 통계적으로 유의미하다는 증거
ANOVA 검정_연습
1. ㅇㅇ회사 마케팅실 그룹별 직원들의 토익성적에 차이가 있는지 알고싶다.
A Group, B Group, C Group 간의 토익 점수의 차이 여부를 검정 (유의수준 0.05)
# ANOVA
df = pd.DataFrame({'A' : [892,623,721,678,723,790,720,670,690,771],
'B' : [721,821,910,678,723,790,711,790,745,891],
'C' : [750,915,888,721,894,834,841,912,845,889]})
# group별 boxplot
df.boxplot(['A','B','C'])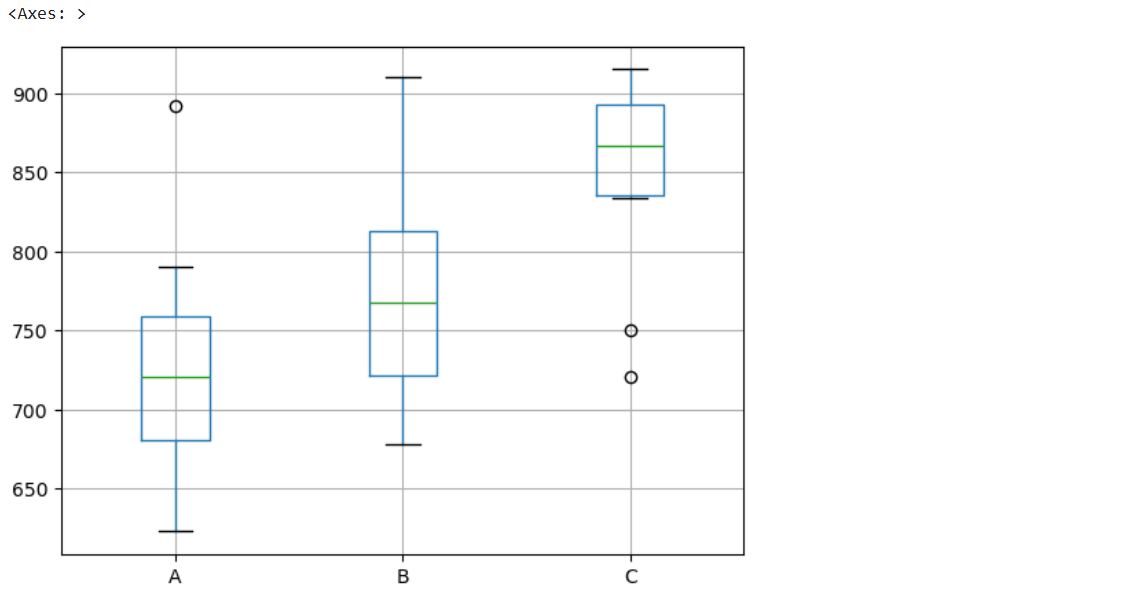
# ANOVA 실행
f_result = stats.f_oneway(df['A'], df['B'], df['C'])
# ANOVA의 f값, p값 저장
f, p = f_result.statistic.round(3), f_result.pvalue.round(3)
# ANOVA의 f값, p값 출력
print('One-way ANOVA')
print('F통계량 : {}'.format(f))
print('p-value : {}'.format(p))
-> 유의수준 5%에서 p-value값이 0.003이므로 그룹간의 토익점수와 평균은 차이가 있다
1-2. 철강의 청정도를 높이기 위해 제강공정에서 2차 정련을 실시하는데,
강종별로 2차 정련시간의 차이가 있는지와 타입별로 2차정련 시간에 차이가 있는지 검정
(유의수준 0.05, data set : ANOVA.csv)
# ANOVA prc2
df = pd.read_csv('ANOVA.csv')
df
# 강종별 ANOVA
anova_gangjong = stats.f_oneway(
df[df['gangjong'] == 'a']['time'],
df[df['gangjong'] == 'b']['time'],
df[df['gangjong'] == 'c']['time'],
df[df['gangjong'] == 'd']['time']
)
print("ANOVA for gangjong:")
print("F-statistic:", anova_gangjong.statistic)
print("P-value:", anova_gangjong.pvalue)
# 타입별 ANOVA
anova_type = stats.f_oneway(
df[df['type'] == 'a']['time'],
df[df['type'] == 'b']['time']
)
print("\nANOVA for type:")
print("F-statistic:", anova_type.statistic)
print("P-value:", anova_type.pvalue)
-> 0.05 보다 작아서 하나 이상 유의미한 차이가 있는데 뭔지를 모르니까 2-sample t-test 로 뭔지 알아내기
# 강종별 그룹 분리
group_a = df[df['gangjong'] == 'a']['time']
group_b = df[df['gangjong'] == 'b']['time']
group_c = df[df['gangjong'] == 'c']['time']
group_d = df[df['gangjong'] == 'd']['time']
# 강종별 2-sample t-test
t_test_ab = stats.ttest_ind(group_a, group_b)
t_test_ac = stats.ttest_ind(group_a, group_c)
t_test_ad = stats.ttest_ind(group_a, group_d)
t_test_bc = stats.ttest_ind(group_b, group_c)
t_test_bd = stats.ttest_ind(group_b, group_d)
t_test_cd = stats.ttest_ind(group_c, group_d)
print("강종별 2-sample t-test 결과:")
print("강종 a vs 강종 b:", "Statistic =", t_test_ab.statistic, "P-value =", t_test_ab.pvalue)
print("강종 a vs 강종 c:", "Statistic =", t_test_ac.statistic, "P-value =", t_test_ac.pvalue)
print("강종 a vs 강종 d:", "Statistic =", t_test_ad.statistic, "P-value =", t_test_ad.pvalue)
print("강종 b vs 강종 c:", "Statistic =", t_test_bc.statistic, "P-value =", t_test_bc.pvalue)
print("강종 b vs 강종 d:", "Statistic =", t_test_bd.statistic, "P-value =", t_test_bd.pvalue)
print("강종 c vs 강종 d:", "Statistic =", t_test_cd.statistic, "P-value =", t_test_cd.pvalue)
# 타입별 그룹 분리
type_a = df[df['type'] == 'a']['time']
type_b = df[df['type'] == 'b']['time']
# 타입별 2-sample t-test
t_test_type = stats.ttest_ind(type_a, type_b)
print("\n타입별 2-sample t-test 결과:")
print("타입 a vs 타입 b:", "Statistic =", t_test_type.statistic, "P-value =", t_test_type.pvalue)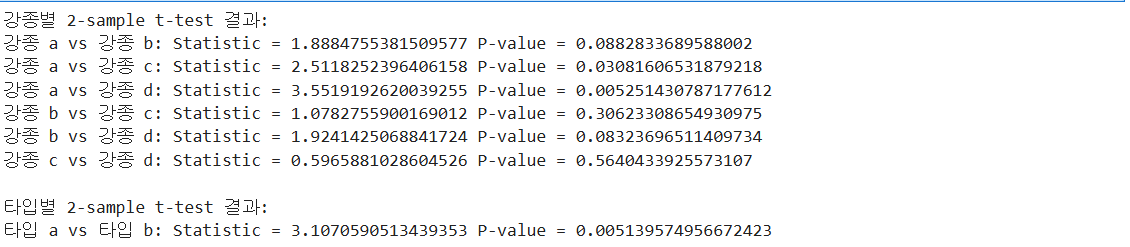
# 강종 a vs 강종 c: p-value = 0.0308 (유의수준 0.05보다 작으므로 차이가 있다고 할 수 있음)
# 강종 a vs 강종 d: p-value = 0.0053 (유의수준 0.05보다 작으므로 차이가 있다고 할 수 있음)
# 타입 a와 타입 b 사이에는 통계적으로 유의한 시간 차이가 있다.
상관분석(Correlation Analysis)
두 변수 간의 선형적 관계의 강도와 방향을 파악하는 통계적 기법
-> 한 변수가 증가할 때 다른 한 변수가 선형적인 증가 또는 감소하는지를 나타낸 것 (산점도 활용)
상관분석에서는 일반적으로 자유도라는 개념은 사용되지 않
상관분석에서 중요한 것은 **상관 계수(Correlation Coefficient)**
선형관계의 척도
- 상관 계수 (Correlation Coefficient):
- 두 변수 간의 선형적 관계를 측정하는 지표로, 주어진 데이터로부터 계산됨
- 두 변수 X와 Y 사이의 선형적 관계를 측정하는 값
- 보통 피어슨 상관 계수(Pearson Correlation Coefficient)사용 (-1에서 1 사이의 값을 가짐)
- 양의 상관 관계: 한 변수가 증가할 때 다른 변수도 증가하는 경우 (상관 계수가 양수)
- 음의 상관 관계: 한 변수가 증가할 때 다른 변수는 감소하는 경우 (상관 계수가 음수)
- 무상관: 두 변수 간에 선형적 관계가 없는 경우 (상관 계수가 0)
- 상관 분석의 목적:
- 변수 간 관계를 이해하고 예측 모델링에 유용한 변수를 선택하는 데 도움을 줌
- 데이터 분석에서 변수 간의 연관성을 확인하여 인사이트를 도출하는 데 사용.
- 주의할 점:
- 상관 분석은 선형적인 관계만을 측정하며, 인과 관계를 설명할 수는 없다.
- 이상치나 비선형적인 관계가 있을 경우 정확한 해석을 제공하지 못할 수 있다.
- 공분산 (Covariance):
- 두 변수 간의 관계를 측정하는 지표
- 공분산은 다음과 같이 정의
- 공분산의 부호는 두 변수 간의 방향성을 나타냄
- 양수일 경우 두 변수가 함께 증가 또는 감소하는 경향이 있으며,
- 음수일 경우 한 변수가 증가하면 다른 변수가 감소하는 경향이 있다.
- 그러나 공분산의 절대값 자체로는 관계의 강도를 정확히 측정하지 못할 수 있다.
상관분석_연습
1. 부품수리시간과 부품수 간에 관계를 분석하기 위한 상관분석을 하세요
df1 = [1,2,3,4,4,5,6,6,7,8]
df2 = [23,29,49,64,74,87,96,97,109,119]
# Correlation Analysis 실행
corr, pval = stats.pearsonr(df1, df2)
# Correlation, p-value 결과 출력
print('Correlation Analysis')
print('corr: {0:0.3f}'.format(corr))
print('p-value : {0:0.3f}'.format(pval))
-> 부품수리시간과 부품수 간의 '매우 강한 상관성'이 있다고 할 수 있다.
1-2. 초코칩의 강도와 재료반죽 온도간에 관계를 분석하기 위한 상관분석을 하세요
strength = [37.6,38.6,37.2,36.4,38.6,39,37.2,36.1,35.9,37.1,36.9,37.5,36.3,38.1,39,36.9,36.8,37.6,33,33.5]
temperature = [14,15,14,16,17,14,17,16,15,16,14,16,18,13,15,17,14,16,20,21]
# Correlation Analysis 실행
corr, pval = stats.pearsonr(strength, temperature)
# Correlation, p-value 결과 출력
print('Correlation Analysis')
print('corr: {0:0.3}'.format(corr))
print('p-value: {0:0.3}'.format(pval))
-> 강도와 재료반죽 온도간의 상관관계 있다.
회귀분석(Regression Analysis)
한 변수(또는 여러 변수)가 다른 변수(들)에 어떤 영향을 미치는지를 분석하는 통계적 방법론
주로 종속 변수(dependent variable)와 독립 변수(independent variable) 사이의 관계를 모델링하고 예측하는 데 사용
종속 변수는 예측하고자 하는 변수이며, 독립 변수는 종속 변수에 영향을 미치는 변수들임
회귀분석의 종류
- 단순 선형 회귀분석(Simple Linear Regression)
- 하나의 독립 변수와 하나의 종속 변수 간의 선형 관계를 분석
- 예를 들어, 집의 크기(X)가 주택 가격(Y)에 어떤 영향을 미치는지 분석 가능
- 다중 선형 회귀분석(Multiple Linear Regression)
- 여러 개의 독립 변수들이 종속 변수에 영향을 미치는지를 분석
- 목표변수가 연속형 변수고 최소자승법, 가중 최소 자승법으로 모델 탐색
- 최소자승법 : 잔차의 제곱합이 최소가 되는 적합선(회귀선) 찾
- 예를 들어, 집의 크기(X1), 위치(X2), 방의 개수(X3) 등이 주택 가격(Y)에 동시에 영향을 미치는지를 분석 가능
- 다항 회귀분석(Polynomial Regression)
- 독립 변수와 종속 변수 사이의 비선형 관계를 모델링
- 예를 들어, 시간(X)에 따른 판매량(Y)을 분석할 때, 시간의 제곱 또는 세제곱 항을 추가하여 모델을 구성 가
- 로지스틱 회귀분석(Logistic Regression)
- 종속 변수가 이항 변수(0 또는 1)인 경우에 사용됩니다.
- 목표변수가 범주형(이산, 순서, 명목) 변수고 최대 우도법으로 모델 탐
- 예를 들어, 고객이 제품을 구매할 확률이 세일 여부에 따라 어떻게 변하는지를 분석 가능
회귀분석의 진행 과정
- 가정 설정(Assumption Setting)
- 데이터의 성격에 맞는 회귀모델을 선택하고 적절한 가정을 설정
- 모델 추정(Model Estimation)
- 선택한 회귀모델을 통해 데이터를 분석하여 회귀계수(coefficient)를 추정
- 모델 평가(Model Evaluation)
- 추정된 모델의 적합성을 평가하고 검정
- 예측 성능, 모델의 유효성, 잔차 분석 등을 통해 모델의 신뢰성을 검증
- 결과 해석(Result Interpretation)
- 추정된 회귀계수의 의미를 해석하고, 독립 변수가 종속 변수에 미치는 영향을 분석
- 가설 검정을 통해 독립 변수가 유의미한지 판단
회귀분석의 장점
- 예측: 다른 변수들의 값을 알 때 종속 변수의 값을 예측 가능
- 인과 관계 분석: 독립 변수가 종속 변수에 어떤 영향을 미치는지를 분석 가능
- 요인 분석: 여러 독립 변수 중에서 어떤 변수가 종속 변수에 가장 큰 영향을 미치는지를 분석 가
- 계수 추정: 회귀분석을 통해 얻은 회귀 계수(coefficient)는 독립 변수가 종속 변수에 얼마나 큰 영향을 미치는지 나타냄 예를 들어, 회귀분석에서 독립 변수 x의 계수가 양수일 경우, x가 증가할 때 종속 변수 y도 증가하는 경향이 있다고 해석 가능
- 변수의 중요도 평가: 다중 회귀분석을 통해 여러 개의 독립 변수 중에서 y에 가장 큰 영향을 미치는 변수를 식별 가능 예를 들어, 제품 판매량을 예측하는 모델에서 가격, 광고 비용, 경쟁사 가격 등 여러 변수 중에서 어느 변수가 판매량에 가장 큰 영향을 미치는지를 분석하여 마케팅 전략을 수립 가능
- 예측 정확도 향상: 회귀분석을 통해 독립 변수와 종속 변수 사이의 관계를 정량화 가능. 이를 통해 기존 데이터를 바탕으로 새로운 데이터에 대한 예측을 더 정확하게 수행할 수 있다. 예를 들어, 고객의 특성(x)이 상품 구매(y)에 얼마나 큰 영향을 미치는지를 분석하여 개별 고객의 구매 가능성을 예측할 수 있다.
다중회귀분석
다중 선형 회귀분석 절차
- 데이터 수집 및 전처리:
- 종속 변수와 여러 개의 독립 변수들을 포함하는 데이터를 수집
- 데이터를 정제하고 결측치 처리, 변수 스케일링 등의 전처리 작업을 수행
- 모델 설정:
- 종속 변수 Y와 독립 변수 X₁, X₂, ..., Xₚ 사이의 관계를 설정하는 선형 회귀 모델을 정의함
- 일반적으로 Y = β₀ + β₁X₁ + β₂X₂ + ... + βₚXₚ + ε 형태로 모델을 설정
- 여기서 ε는 오차를 나타냄
- 선형회귀분석을 하려면 이론상 오차는 독립, 등분산성, 정규성 만족해야함 .
- 회귀계수 추정:
- 주어진 데이터를 사용하여 최소자승법(Least Squares Method)을 이용해 회귀계수(β₀, β₁, β₂, ..., βₚ)를 추정
- 추정된 회귀계수는 각 독립 변수가 종속 변수에 미치는 영향의 방향과 크기를 나타냄
- 모델 적합성 평가:
- 회귀 모델의 적합성을 평가하기 위해 결정계수(R²)나 수정된 결정계수, 추정의 표준오차(Se = 잔차들의 표준편차), ANOVA 검정(분산분석의 F-검정을 활용해 유의성 검정) 을 통해 모델이 데이터를 얼마나 잘 설명하는지 평가
- 이 과정에서 모델이 데이터에 과적합(overfitting)되지 않았는지 확인하는 것이 중요
- 다중공산성(Multicollinearity) 검사:
- 독립 변수들 간의 상관 관계가 너무 강해서 모델에서 문제를 일으킬 수 있는 다중공산성을 검사
- 다중공산성을 확인하기 위해 VIF(Variance Inflation Factor) 등의 지표를 사용
- 잔차 가정 확인:
- 회귀 모델의 잔차(residuals)가 정규성, 등분산성, 독립성을 만족하는지 확인
- 경향선 없이 무작위로 찍히면 등분산성을 만족한다.
- 잔차가 정규분포를 따르는지 확인하는 Q-Q plot, 잔차의 등분산성을 검사하는 방법 등을 사용
회귀계수 계산
회귀분석에서는 최소자승법(OLS, Ordinary Least Squares)을 사용하여 회귀계수를 추정
(자료를 적합하는 직선 무수히 많음 -> 어떤 적합선을 선택할건지 -> 예측값과 실제값 차이를 최소회하는 적합선 탐색
: 잔차는 적합선 상의 예측값(직선 위의 값)과 실제 관측값과의 차이
: 잔차의 제곱합이 최소가 되는 적합선을 찾는 방법
1. 잔차제곱합 2. 잔차제곱합의 최소화, 3. 절편과 기울기의 편미분 4.절편과 기울기값 도출)
각 독립 변수의 회귀계수는 종속 변수와의 관계를 설명하는 중요한 지표다.
회귀계수는 회귀모델을 통해 추정된 변수들 간의 관계의 방향성과 강도를 나타냄
다중공산성(Multicollinearity) 확인
다중공산성은 독립 변수들 간의 강한 상관 관계로 인해 회귀 모델이 부정확하거나 불안정해지는 현상
다중공산성을 확인하기 위해 VIF(Variance Inflation Factor)를 사용
일반적으로 VIF가 10 이상이면 다중공산성이 존재한다고 판단 가능
모델적합성 확인
모델적합성은 회귀 모델이 주어진 데이터를 얼마나 잘 설명하는지를 평가하는 것
주로 결정계수(R²)를 사용하여 모델이 데이터를 얼마나 잘 설명하는지를 평가
R² 값이 클수록 모델이 데이터를 잘 설명한다고 할 수 있다.
결정계수가 음수가 나온 경우 셔플 or 랜덤값으로 test data 섞기
잔차 가정 확인
잔차(residuals)는 회귀모델에서 관측값과 예측값의 차이를 의미
잔차가 회귀모델의 가정을 만족하는지 확인하는 것은 모델의 신뢰성을 평가하는 중요한 과정
정규성, 등분산성, 독립성 등의 가정을 만족하지 않는 경우, 모델의 해석이나 예측력이 떨어질 수 있다.
-> 결정계수 x변수 의미 없든있든 많아지면 무조건 커짐
수정 결정계수 : 의미있는 x변수만
데이터분할 : .train_test_split(test_size, shuffle, random_state)
모델 훈련 : 적용모델.fit(X, Y)
모델 적용 : 적용모델.predict(X) -> fit으로 생성된 모델에 test 데이터(X)를 입력하여 모델의 값 예측
결과예측 : score -> 회귀모델에서 사용시 결정계수 반환, 분류모델에서 사용시 정확도 반환
상관계수 계산 : pandas.DataFrame.corr
회귀분석 : OLS
다중선형 회귀분석_연습
# 다중선형 회귀분석_연습
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from statsmodels.api import qqplot, add_constant
import statsmodels.formula.api as smf
from statsmodels.tools.eval_measures import rmse
from sklearn.metrics import r2_score
from statsmodels.stats.outliers_influence import variance_inflation_factorimport matplotlib
matplotlib.rc('font', family='Malgun Gothic')
matplotlib.rc('axes', unicode_minus=False)
# 그래프 출력
%matplotlib inline
# 실행결과 경고메시지 출력 제외
import warnings
warnings.filterwarnings('ignore')df_raw = pd.read_csv('body.csv')
df_raw.head()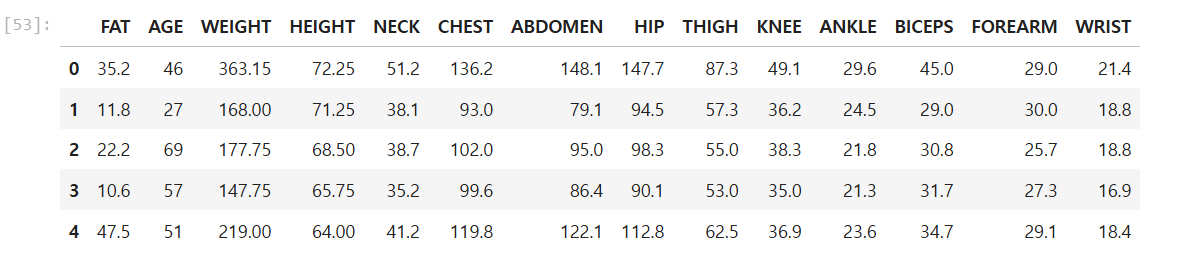
# 2. 변수간의 경향성 파악 - 그래프 분석
# 산점도 행렬
sns.pairplot(df_raw, y_vars = 'FAT', x_vars = ['WEIGHT', 'NECK', 'CHEST', 'ABDOMEN'])
# 회귀 적합선 추가 : kind = 'reg'
sns.pairplot(df_raw, y_vars = 'FAT', x_vars = ['WEIGHT', 'NECK', 'CHEST', 'ABDOMEN'], kind = 'reg')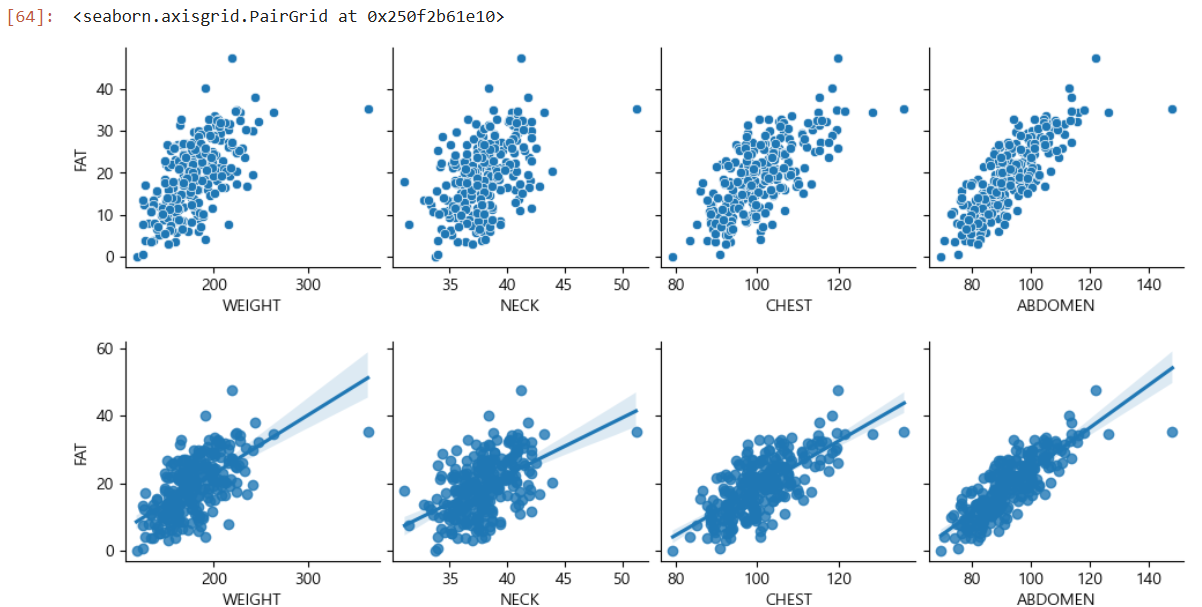
# 2. 변수간의 경향성 파악 - 그래프 분석
# 산점도 행렬
sns.pairplot(df_raw)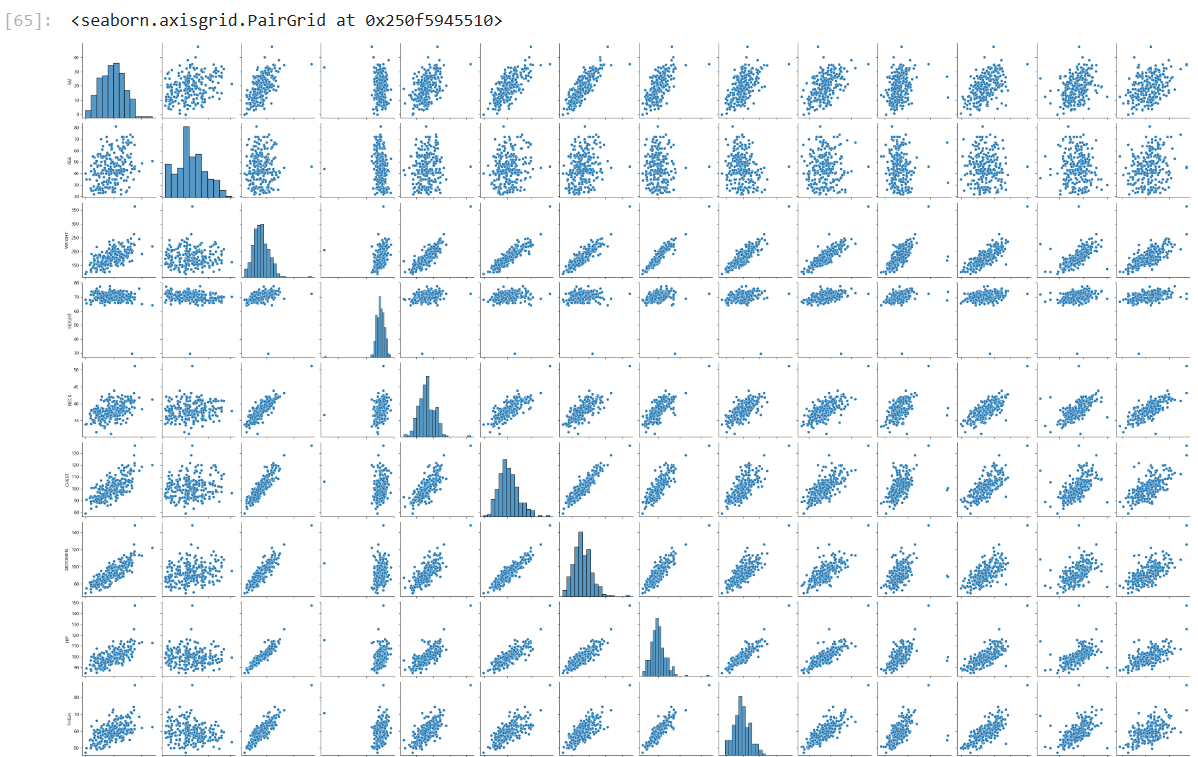
# 2. 변수간의 경향성 파악 - 상관관계 분석
df_raw.corr().round(3)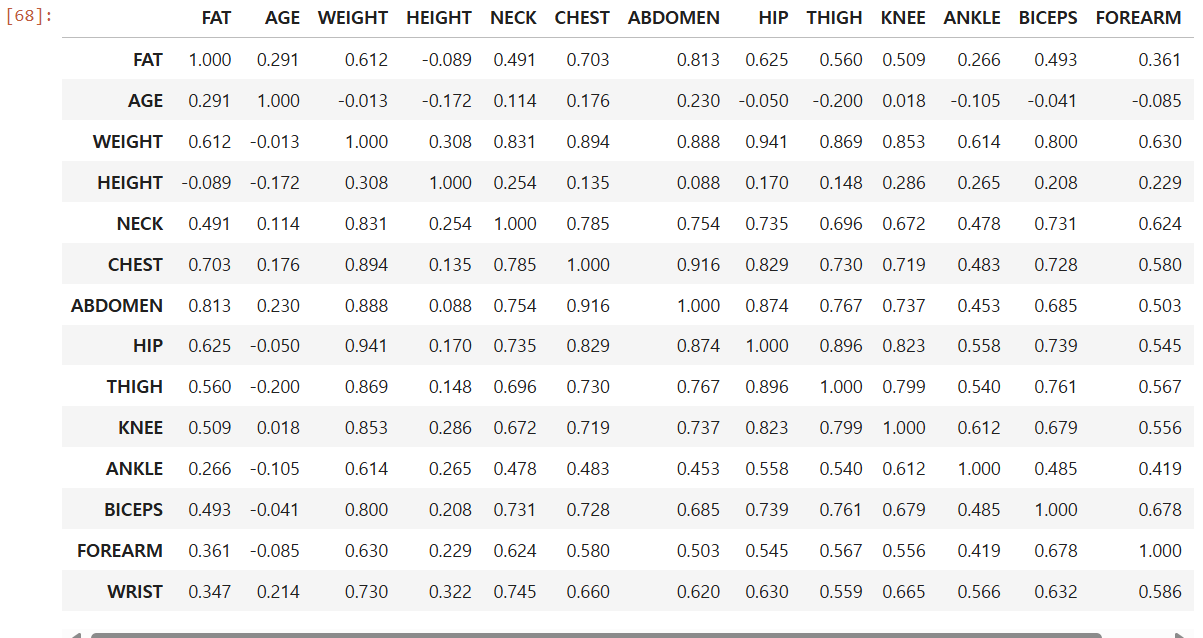
# 3. 회귀모델 생성 : 설명변수 전체
# 학습용 / 평가용 데이터 분리
df_train, df_test = train_test_split(df_raw, test_size = 0.3, random_state = 1234)
print('학습용 데이터 크기 : {}'.format(df_train.shape))
print('평가용 데이터 크기 : {}'.format(df_test.shape))
# 3. 회귀모델 생성 : 설명변수간의 다중공산성 확인
df_raw_x = df_train[['WEIGHT', 'ABDOMEN', 'FOREARM', 'WRIST']]
# statsmodels의 상수항 추가 함수 적용
df_raw_x_const = add_constant(df_raw_x)
# DataFrame으로 저장
df_vif = pd.DataFrame()
df_vif['variable'] = df_raw_x_const.columns
df_vif['VIF'] = [variance_inflation_factor(df_raw_x_const.values, i) for i in range(df_raw_x_const.shape[1])]
# VIF 정렬
df_vif.sort_values('VIF', inplace = True)
df_vif.round(3)
# 3. 회귀모델 생성 : 유의하지 않은 변수 제거 (p-value < 0.05 변수 선택)
# 선형회귀분석
reg_model = smf.ols(formula = 'FAT ~ AGE + WEIGHT + HEIGHT + NECK + CHEST+ ABDOMEN \
+ HIP + THIGH + KNEE + ANKLE + BICEPS + FOREARM + WRIST', data = df_train)
# 적합
reg_result = reg_model.fit()
print(reg_result.summary())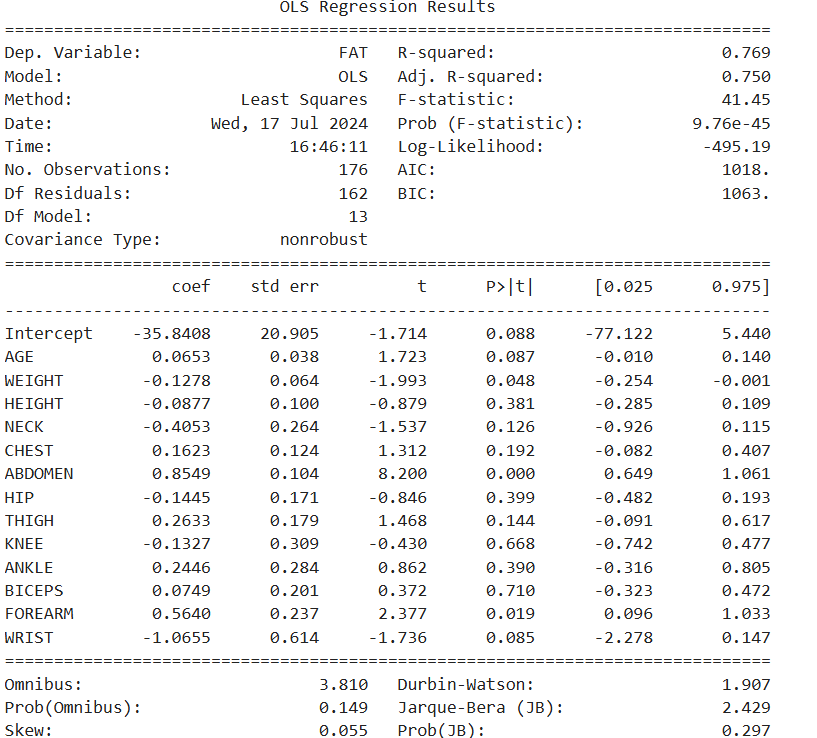
# 3. 회귀모델 생성 : 유의하지 않은 변수 제거 (p-value < 0.05 변수 선택)
# 선형회귀분석
reg_model = smf.ols(formula = 'FAT ~ AGE + WEIGHT + HEIGHT + NECK + CHEST+ ABDOMEN \
+ HIP + THIGH + KNEE + ANKLE + FOREARM + WRIST', data = df_train)
# 적합
reg_result = reg_model.fit()
print(reg_result.summary())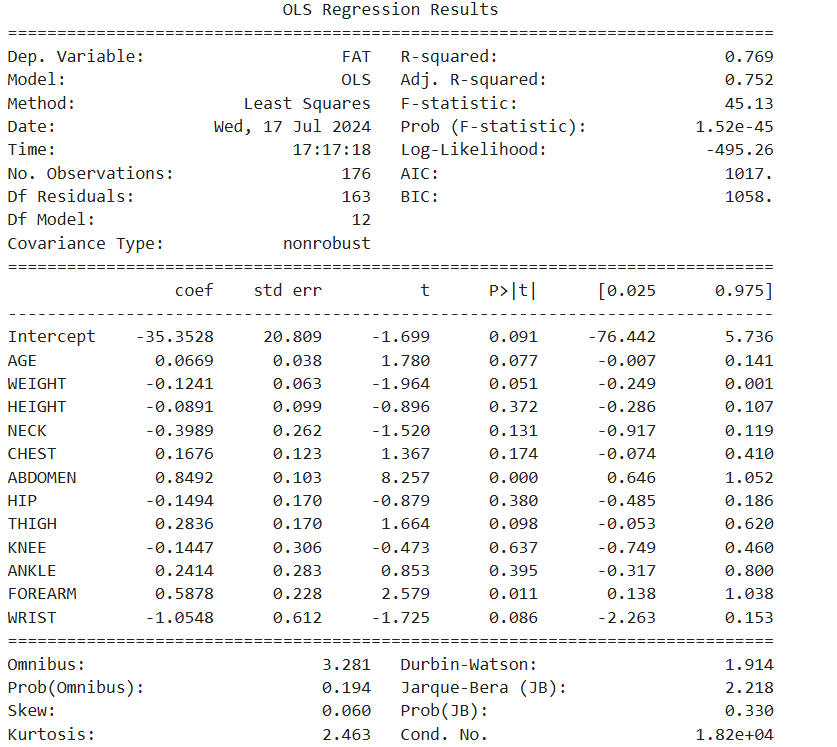
# 3. 회귀모델 생성 : 유의하지 않은 변수 제거 (p-value < 0.05 변수 선택)
# 선형회귀분석
reg_model = smf.ols(formula = 'FAT ~ AGE + WEIGHT + HEIGHT + NECK + CHEST+ ABDOMEN \
+ HIP + THIGH + ANKLE + FOREARM + WRIST', data = df_train)
# 적합
reg_result = reg_model.fit()
print(reg_result.summary())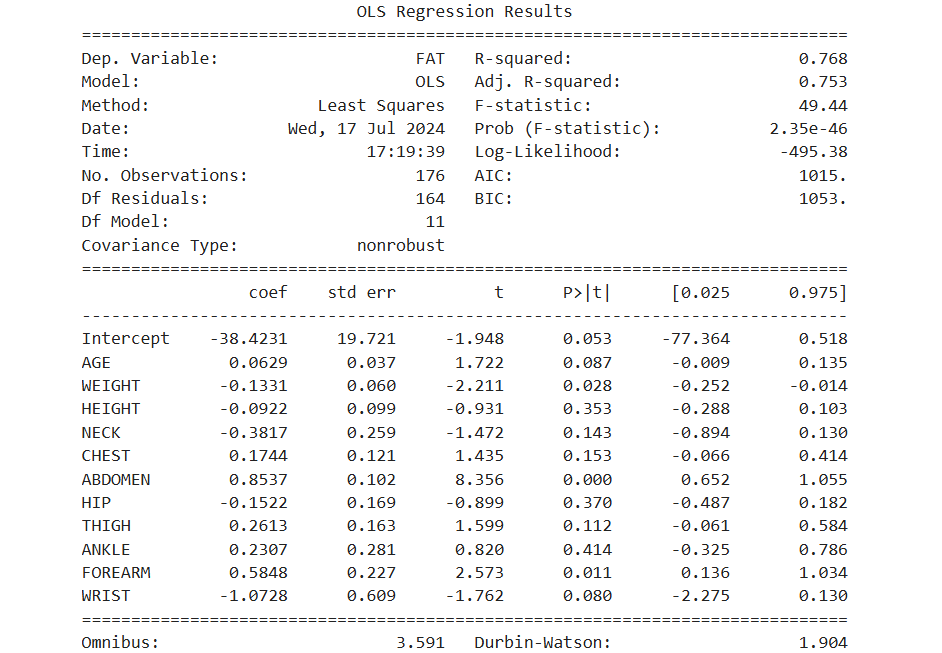
# 3. 회귀모델 생성 : 유의하지 않은 변수 제거 (p-value < 0.05 변수 선택)
# 선형회귀분석
reg_model = smf.ols(formula = 'FAT ~ AGE + WEIGHT + HEIGHT + NECK + CHEST+ ABDOMEN \
+ HIP + THIGH + FOREARM + WRIST', data = df_train)
# 적합
reg_result = reg_model.fit()
print(reg_result.summary())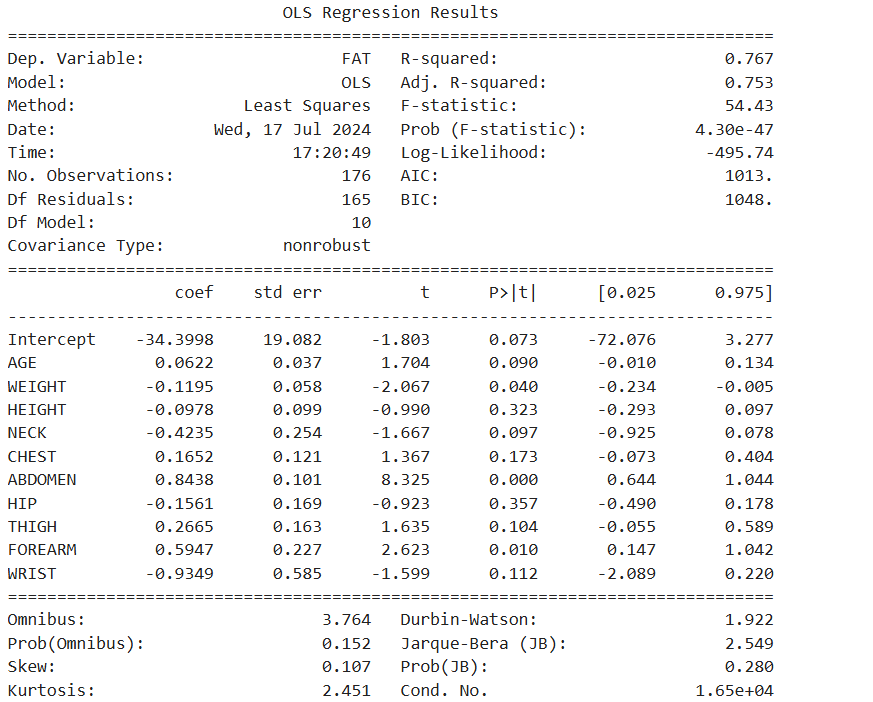
# 3. 회귀모델 생성 : 유의하지 않은 변수 제거 (p-value < 0.05 변수 선택)
# 선형회귀분석
reg_model = smf.ols(formula = 'FAT ~ AGE + WEIGHT + HEIGHT + NECK + CHEST+ ABDOMEN \
+ THIGH + FOREARM + WRIST', data = df_train)
# 적합
reg_result = reg_model.fit()
print(reg_result.summary())
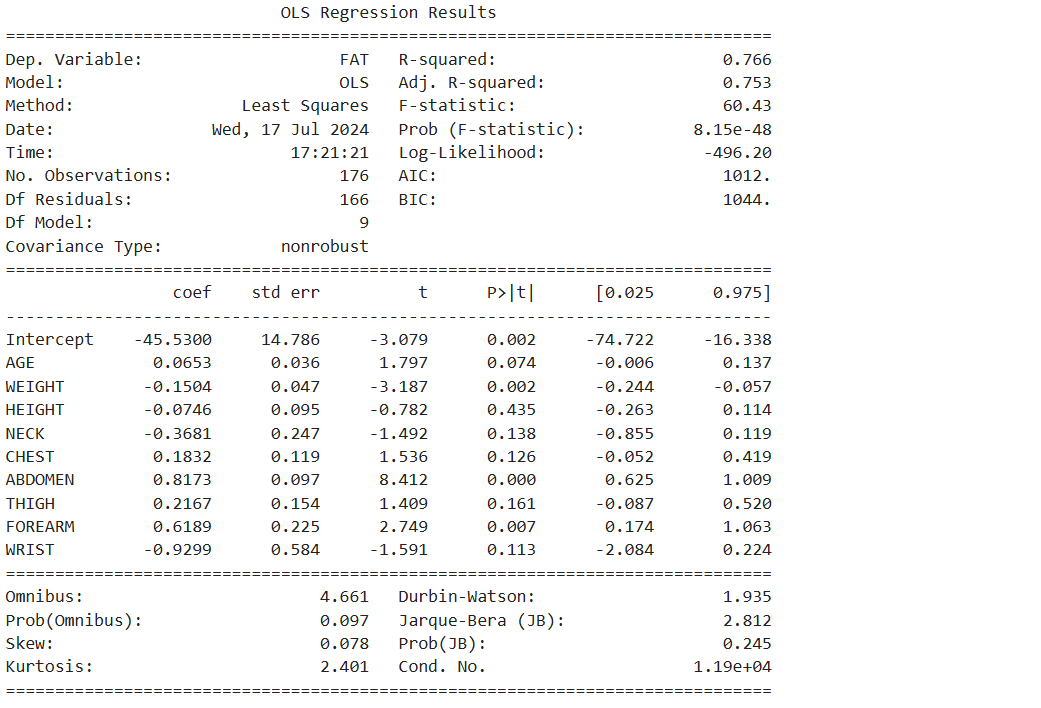
# 3. 회귀모델 생성 : 유의하지 않은 변수 제거 (p-value < 0.05 변수 선택)
# 선형회귀분석
reg_model = smf.ols(formula = 'FAT ~ AGE + WEIGHT + NECK + CHEST+ ABDOMEN \
+ HIP + THIGH + FOREARM + WRIST', data = df_train)
# 적합
reg_result = reg_model.fit()
print(reg_result.summary())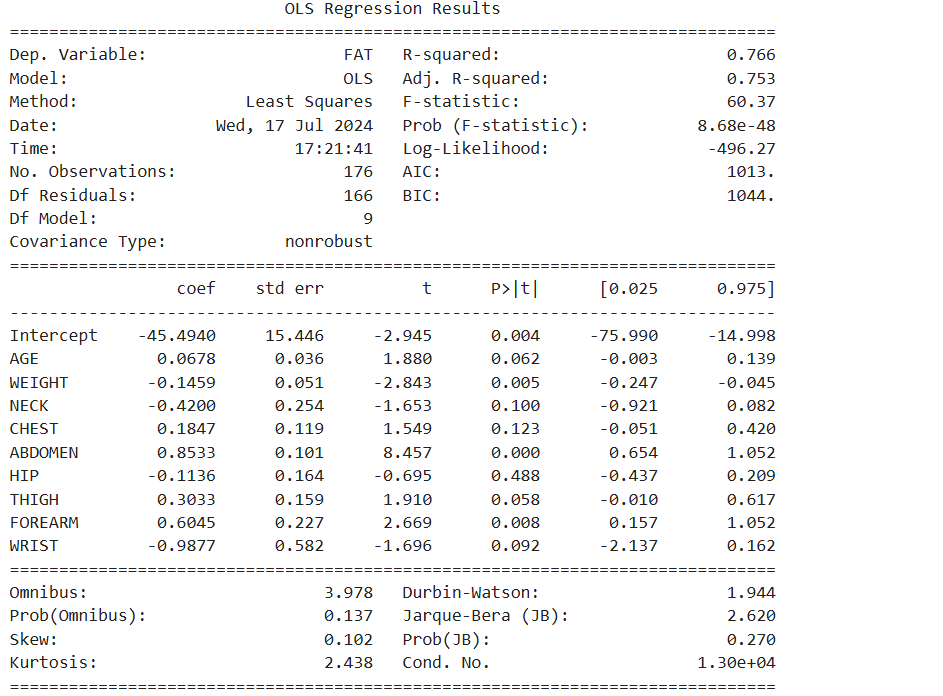
# 3. 회귀모델 생성 : 유의하지 않은 변수 제거 (p-value < 0.05 변수 선택)
# 선형회귀분석
reg_model = smf.ols(formula = 'FAT ~ AGE + WEIGHT + HEIGHT + NECK + CHEST+ ABDOMEN \
+ THIGH + FOREARM + WRIST', data = df_train)
# 적합
reg_result = reg_model.fit()
print(reg_result.summary())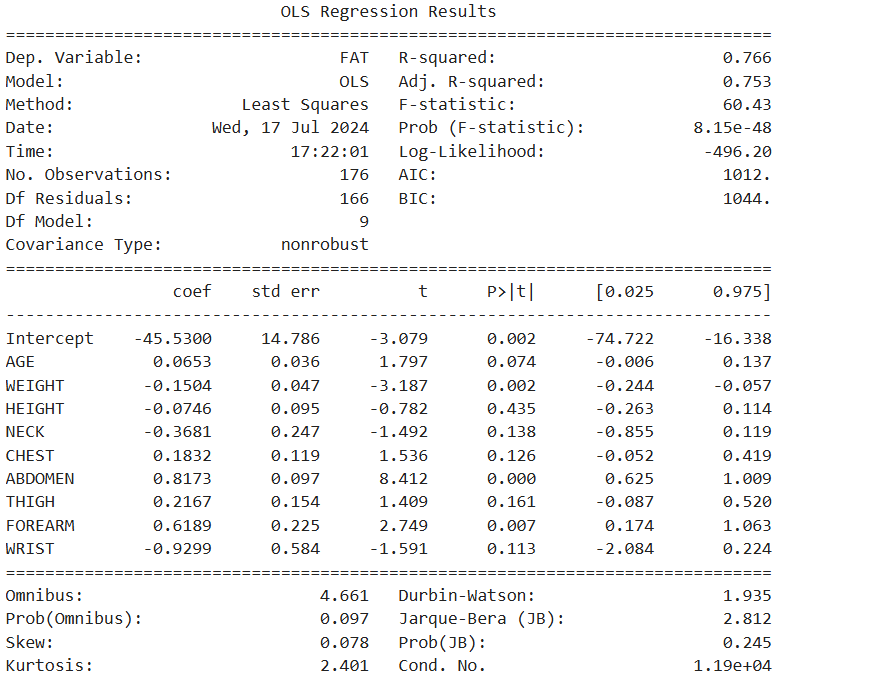
# 3. 회귀모델 생성 : 유의하지 않은 변수 제거 (p-value < 0.05 변수 선택)
# 선형회귀분석
reg_model = smf.ols(formula = 'FAT ~ AGE + WEIGHT + NECK + CHEST+ ABDOMEN \
+ THIGH + FOREARM + WRIST', data = df_train)
# 적합
reg_result = reg_model.fit()
print(reg_result.summary())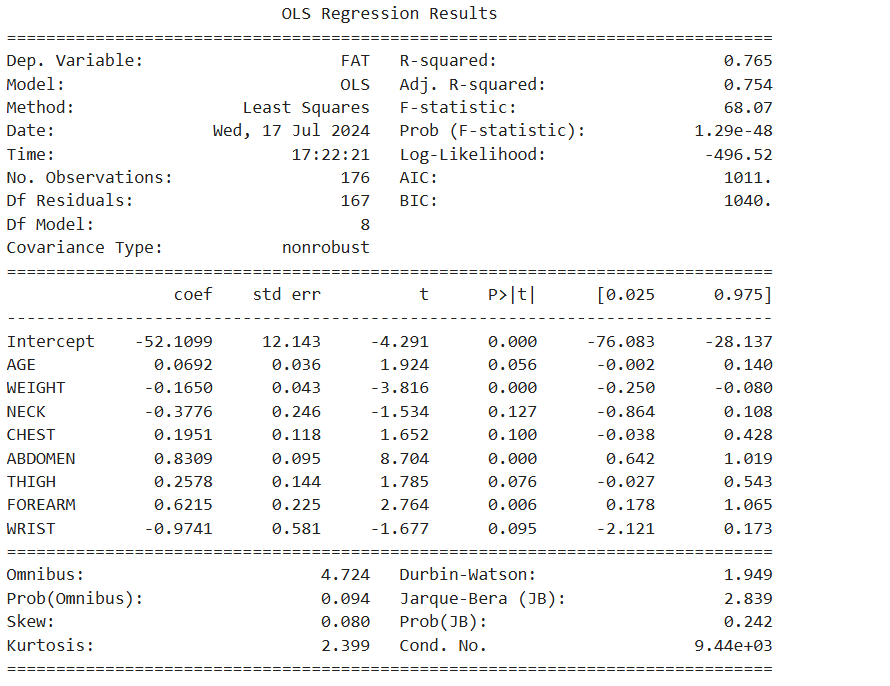
# 3. 회귀모델 생성 : 유의하지 않은 변수 제거 (p-value < 0.05 변수 선택)
# 선형회귀분석
reg_model = smf.ols(formula = 'FAT ~ AGE + WEIGHT + CHEST+ ABDOMEN \
+ THIGH + FOREARM + WRIST', data = df_train)
# 적합
reg_result = reg_model.fit()
print(reg_result.summary())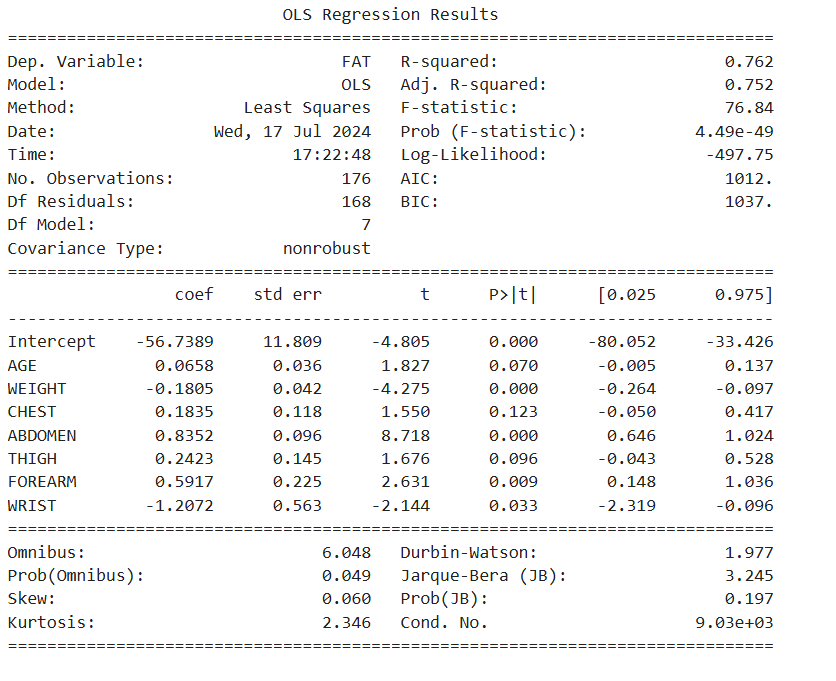
# 3. 회귀모델 생성 : 유의하지 않은 변수 제거 (p-value < 0.05 변수 선택)
# 선형회귀분석
reg_model = smf.ols(formula = 'FAT ~ AGE + WEIGHT + ABDOMEN \
+ THIGH + FOREARM + WRIST', data = df_train)
# 적합
reg_result = reg_model.fit()
print(reg_result.summary())
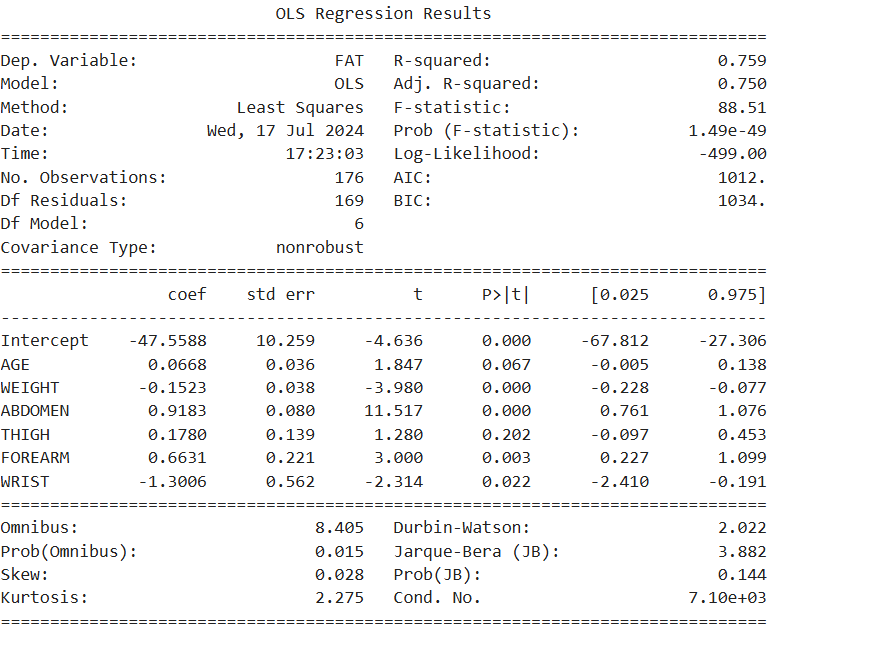
# 3. 회귀모델 생성 : 유의하지 않은 변수 제거 (p-value < 0.05 변수 선택)
# 선형회귀분석
reg_model = smf.ols(formula = 'FAT ~ AGE + WEIGHT + ABDOMEN + FOREARM + WRIST', data = df_train)
# 적합
reg_result = reg_model.fit()
print(reg_result.summary())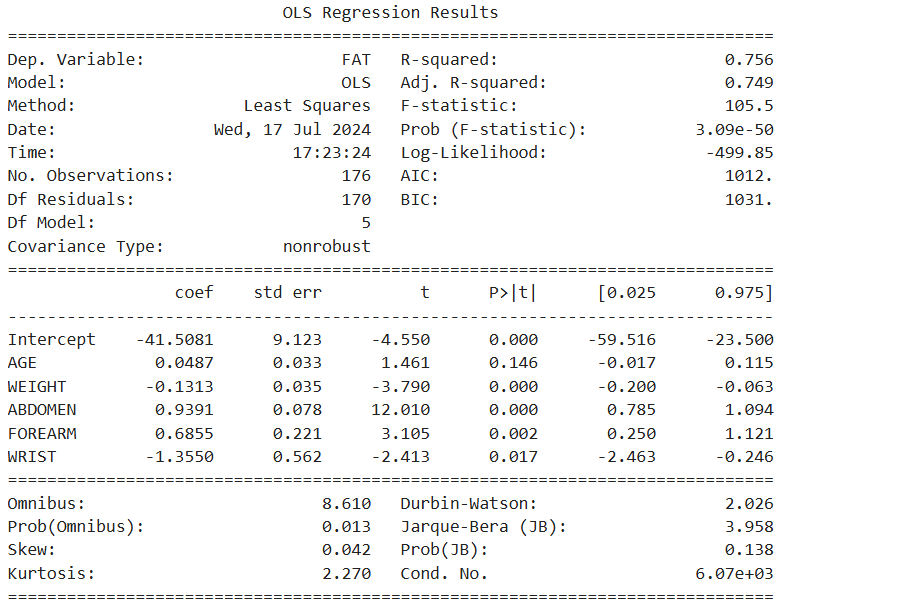
# 3. 회귀모델 생성 : 유의하지 않은 변수 제거 (p-value < 0.05 변수 선택)
# 선형회귀분석
reg_model = smf.ols(formula = 'FAT ~ WEIGHT + ABDOMEN + FOREARM + WRIST', data = df_train)
# 적합
reg_result = reg_model.fit()
print(reg_result.summary())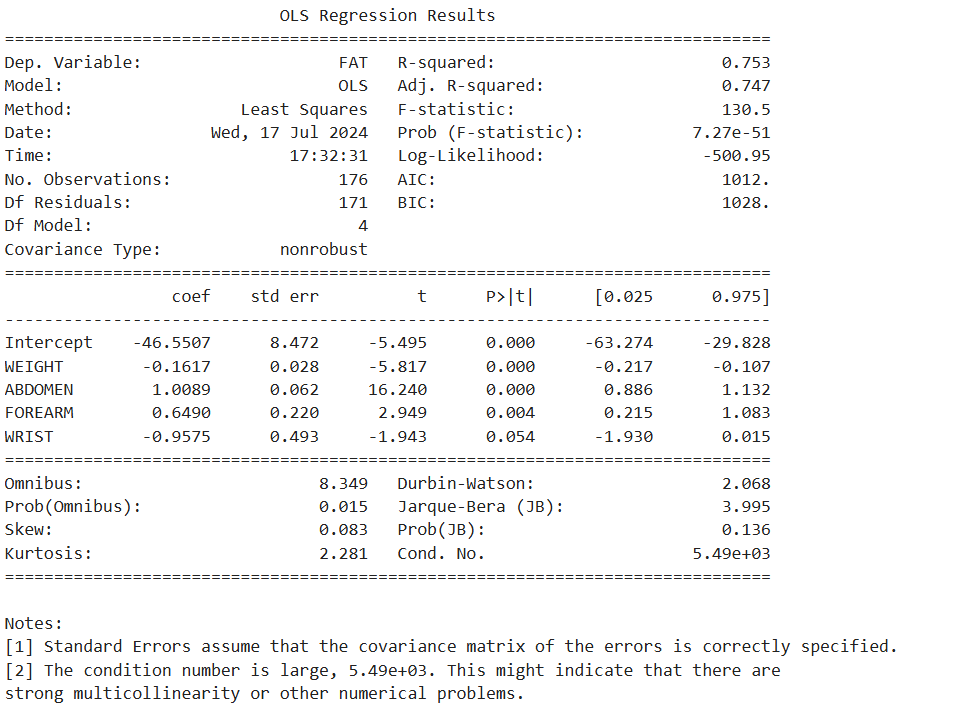
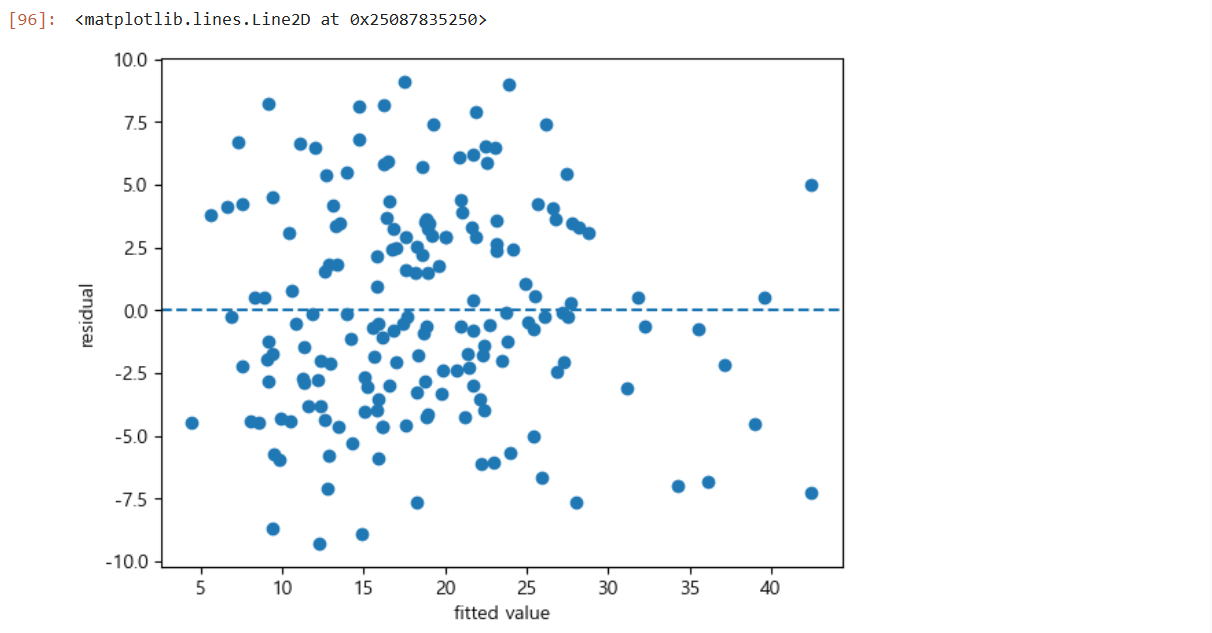
# 4. 오차의 기본가정 검토
# 잔차의 등분산성 : X - 예측값, Y - 잔차
plt.scatter(reg_result.fittedvalues, reg_result.resid)
plt.xlabel('fitted value')
plt.ylabel('residual')
plt.axhline(y = 0, linestyle = '--')
# 잔차가 y = 0을 기준으로 Random하게 산포되어 있으므로 등분산성 만족
# 독립성 검정
# 잔차의 독립성 : X-데이터순서, Y-잔차
plt.scatter(df_train.index, reg_result.resid, marker = 'o')
plt.xlabel('Data')
plt.ylabel('residual')
plt.axhline(y = 0, linestyle = '-')
plt.axhline(y = 3 * np.std(reg_result.resid), linestyle = '--')
plt.axhline(y = -3 * np.std(reg_result.resid), linestyle = '--')
# 잔차가 관리도의 관리기준을 초과하는 데이터가 없고 경향성이 없으므로 독립성 만족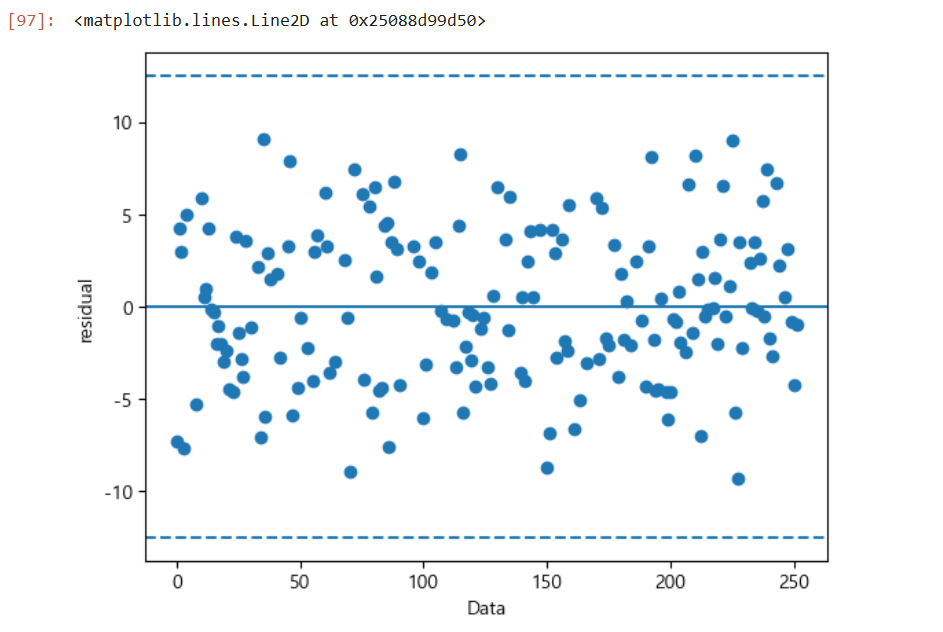
# 4. 오차의 기본가정 검토
# 정규성 검정
# 잔차 정규성 검정 : Q-Q plot
qqplot(reg_result.resid, line = 'q')
# 잔차항이 정규분포를 따르는지 검정
# 정규확률도의 각 점들이 직선을 따라 분포하므로 정규분포를 따르는 것으로 판단
# -> 실제 검정 결과에도 정규성을 따르는 것으로 도출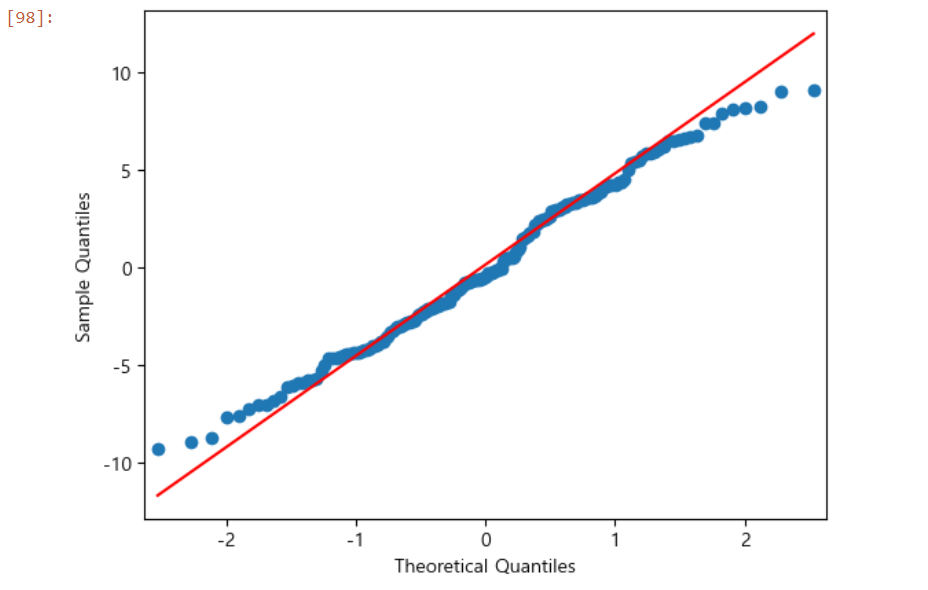
# 최종 도출
# 최종 모델의 회귀식
# FAT = -46.55 - 0.16WEIGHT + 1.01 ABDOMEN + 0.65 FOREARM - 0.96 WRIST# 결론도출
# 변수중요도 확인
# 설명변수 중요도
selected_cols = ['WEIGHT', 'ABDOMEN', 'FOREARM', 'WRIST']
df_reg_coef = pd.DataFrame({'Coef': reg_result.params[selected_cols]}, index=selected_cols)
df_reg_coef.plot.barh(y='Coef', legend=False)
# 중요도는 회귀계수의 절대값 크기
# 손목 두께가 얇을수록 비만도 높음, 복부둘레 커질수록 비만도 높음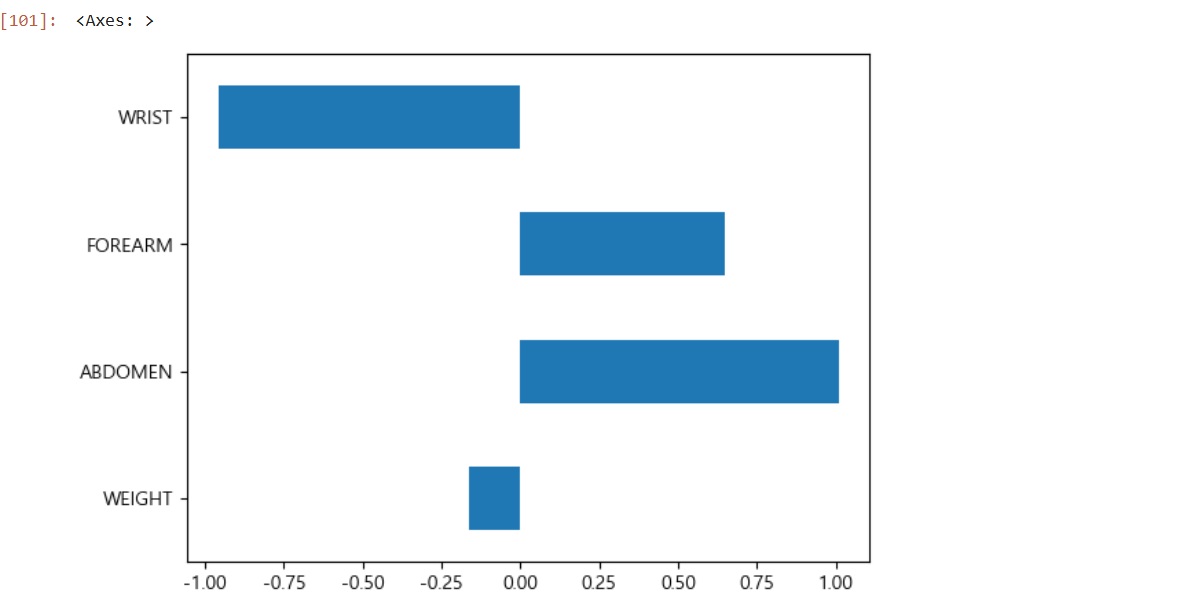
# 평가용 데이터 결정계수 확인
y_pred = reg_result.predict(df_test)
print('평가용 데이터의 설명력 : ', r2_score(df_test['FAT'], y_pred))
'파이썬 & 머신러닝과 딥러닝' 카테고리의 다른 글
| 데이터 정규화, 표준화, 백분위수, 주성분 분석 (PCA), 회귀분석, 회귀 성능 평가(MAE, MSE, RMSE, R² 스코어) (1) | 2024.08.08 |
|---|---|
| 통계적 공정관리 (0) | 2024.07.19 |
| 통계의 이해(기술통계, 확률분포, 중심극한정리, 추론통계, 구간추정, 가설검정, 정규성검정, 평균검정) (0) | 2024.07.16 |
| 데이터 수집 및 정제 (데이터 결합, 데이터 변환, 데이터 정제), 시각화 (0) | 2024.07.15 |
| 파이썬 분석 도구 및 주요 함수의 이해, 데이터 수집 및 정제 (데이터 선택) (1) | 2024.07.12 |



