파이썬 머신러닝 완벽 가이드(권철민) - 딥러닝x , 머신러닝의 추천 시스템(인프런에 강의 O)
KNN
- C - wqistic R (분류)
- R - Linear R (회귀)
회귀는 선을 그어 수치를 예측하는 것
3-1 K-최근접 이웃 회귀
농어의 무게를 예측하라
- 농어의 정보(길이, 높이, 두께)로 농어의 무게 예측
지도 학습 알고리즘
- 분류 : 도미와 빙어를 구분하는 문제
(2진 분류, 3진 분류, N진 분류)
- 회귀 : 임의의 어떤 수치(농어의 무게)를 예측하는 것
(타겟 : 임의의 숫자값)
회귀 : 두 변수 x, y사이의 상관관계를 분석하는 방법
x와 y사이를 나타내는 회귀 : 최적의 선식을 구한다.
(x가 독립변수 y가 종속변수 (ex) x축이 공부 시간, y축이 성적) )
일차 함수식이 y = f(x)에서 y=f(i,j,k,l,m....) 이 된다. -> 관계를 묘사하는 선식(직선)을 찾아야한다.
K-최근접 이웃 회귀
k-최근접 이웃 분류는 KNN에서 가장 가까운 k개 샘플을 선택해 다수결을 결과 클래스로 예측
k-최근접 이웃 회귀는 KNN에서 가장 가까운 k개 샘플 값의 평균
농어(peach)의 길이로 무게 예측
하나의 특성으로 하나의 타겟 예측해보자
-> 농어의 길이만을 사용하여 무게를 예측
길이와 무게 데이터를 넘파일 배열로 변환
특성 중 하나, 이 경우 weight를 타겟으로

훈련 세트 준비
훈련세트와 테스트 세트의 구분
2차원 리스트 형태로 데이터 변환
(사이킷런에 사용할 데이터 세트는 2차원 배열이여야 함.)

크기 인자 -1 지정 -> 나머지 원소 개수로 모두 채우라는 의미
reshape() : 배열 차원 변환 넘파이 함수
회귀는 임의의 숫자가 타겟이 되기 때문에
stratify (비율 고르게 해달라는 함수) 값 사용하지 않는다.
회귀 모델 훈련
회귀 모델과 결졍 계수 (R^2)
회귀 문제의 score() 결과값은 결정 계수
결정계수(R^2)
score점수 99.28% 맞혔다가 백분율이 아니라 결정계수
-> 회귀에서 score은 결정계수
(회귀 모델의 정확도는 사실상 정확한 값을 맞추기 어려워 결정계수 사용)
(분류 모델의 정확도 : 맞은 개수(%))



mean_absolute_error (또 다른 측정 도구) : 평균 절대값 오차
(입력으로 준 모든 데이터에 대해서 오차를 평균 절대값으로 출력)
test_target과 test_prediction 사이의 오차를 mae에 넣어서 출력
-> 평균적으로 19g의 오차가 발생 (직관적 이해 용이)
분류, 회귀 시스템의 정확도를 평가하는 다양한 방법
분류 - Accuracy(%), precision, recall, F1 score, Roc(Auc)
회귀 - R^2, MAE, MSE, RMSE, MAPE(MAE의 백분율)
과대 적합과 과소 적합
훈련 데이터와 테스트 데이터의 결정 계수(score 점수)를 확인해보기
k-최근접 이웃 회귀 모델의 결정 계수 결과값에 대한 고찰
일반적으로 테스트 점수가 좀 더 낮은게 일반적 (시험 예상 문제와 실전 문제)
하지만, 아래 결과 테스트 점수가 더 높음 (train은 96인데 test는 99)

과대 적합 : 훈련 점수가 더 좋은데 테스트 점수가 안좋은 것 (너무 복잡해서 단순화 하기)
과소 적합 : 훈련 점수가 안좋은데 운좋게 테스트 점수가 좋은 것 or 둘 다 낮은 것 (너무 단순화된 상태)

이웃 개수 줄이기
이웃의 개수가 많은게 단순한 것 -> 이웃의 개수가 많으면 평균으로 예측하게 됨 (일반화)
현 상황 과소 적합에서 이웃 개수 줄이기 (이웃의 개수가 줄인게 복잡한 것)

-> 이웃의 개수가 줄이니 훈련 세트 점수가 더 좋아짐
과대 적합 : 이웃의 개수가 적으면 국지적 패턴에 민감 -> 훈련세트에만 최적화
과소 적합 :이웃의 개수가 많으면 일반화가 된다
-> 전체 이웃의 개수를 사용하면 하나의 값만 예측됨(훈련세트 학습이 되지 않은 상태)
최적의 이웃의 개수 n 구하는 방법?
하이퍼파라미터 결정법 (5장)
확인 문제
이웃의 개수를 조정해가면서 선식(예측 결과 그래프)을 그리기

3-2 선형 회귀
아주 큰 농어
최근접 이웃 회귀의 문제점
길이가 50일 때(혹은 100일 대) 무게 얼마?


최근접 이웃 회귀 vs (일반적) 선형 회귀
50cm 농어의 이웃
최근접 이웃 회귀의 한계를 살펴보자

-> 위 코드 설명
넘파이 데이터 준비, 훈련세트와 테스트 구분
knr 모델 객체 선언 (이웃개수 3)
훈련(fit) 수행 및 50cm 무게 예측 -> 1033g


45cm 보다 크면 이웃이 무조건 3개 밖에 안됨
-> 최근접 이웃 회귀는 가까운 이웃을 선정하고 이웃들의 평균값으로 예측함
-> 훈련세트 샘플 범위 밖의 값을 예측하기가 힘들다
-> K-최근접 이웃 회귀를 선형 회귀로 극복
선형 회귀 (linear regression)
: 특성이 하나인 경우, 어떤 직선을 학습하는 것
이러한 직선을 찾는 것 : 선형 회귀


직선의 방정식을 구하는 것은 결국 직선 방정식에서 a, b를 찾는 과정

lr.coef_, lr.intercept_ : 직선 식을 찾는 것
참고) Scikit-learn.org에서 해당 속성(Attribute) 확인
식이 있으면 절편은 하나,
계수는 여러개 가능 -> 리스트 형태
학습하나 값을 모델 객체에 저장시, 속성 이름 끝에 _ 추가
즉, 지정한 값이 아닌 학습한 값 -> 모델 파라미터 (인공지능이 찾은 값)
파라미터
- 모델 파라미터 (_붙은 Attribute : 인공지능이 학습해서 절편을 알아내는 것),
- 하이퍼 파라미터 (이웃을 몇 개로 할 때 최적의 결과가 나오는지 정답이 없고 설계자가 직접 설정)
Out = ax + by + cz +d 일 경우도 가능
즉, 속성이 여러 개일 경우
-> 다중 회귀(x, y...) : 항이 여러개, 직선(곡선 x)),
다항 회귀(x, x^2...) : 고차항
다중 다항 회귀 : 여러개의 특성(feature)이 다항으로 있는 경우 정교화 가능(과대 적합)
학습한 직선 그리기

-> 학습한 직선 식과 일치하는구나를 알 수 있음
-> 두 점수가 너무 낮게 나옴 : 과소 적합
문제 1) 두 점수 모두 낮고, 특히 테스트 세트에서 R^2 점수가 너무 낮은 상태 (과소 적합)
문제 2) 15보다 작으면 무게가 음수? 추가 개선 필요 -> 선형을 곡선으로 (이차함수가 좀 더 정교)
-> 고차항을 넣는 다항식이 필요하다 : 다항 회귀
다항 회귀 (polynomial regression)
최적의 직선을 찾기 보다 최적의 곡선을 찾자
x의 다항식을 이용한 회귀 (제곱항, 세제곱항 등)


-> 길이의 제곱항을 추가
column_stack() : 1차원 배열을 열방향으로 붙임 (넘파이 브로드캐스팅 연산 적용)
다항회귀에서 이차 방정식은 곡선인데 선형 회귀? Yes
일반적으로 이를 모두 선형 회귀라 함
x^2항을 다른 1차 변수로 치환하여 표현하면
그래프는 곡선이지만, 식상으로는 1차항만 존재하는 선형이라고 볼 수 있음
모델 다시 훈련

-> 다항 입력 형태로 예측값 준비시 1.251kg -> 1.573kg 예측
제곱항 추가로 계수(coef)가 2개 (리스트 형태)
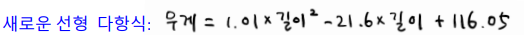
학습한 직선 그리기

-> predict() 가 예측한 무게값을 그려서 회귀 곡선과 비교
arange() : 인덱스 생성 함수 (짧은 직선을 이어 곡선으로 표기)

R^2 점수 확인
아직 테스트 점수가 조금 더 높다 (과소 적합이 남아있는 상태, test가 더 높으면 안된다.)
-> 조금 더 복잡한 모델 필요 (학습이 더 필요)
정리)
사례 기반 학습
: K-최근접 이웃에는 모델 파라미터가 없음 -> 사례 기반 학습
단순히 기존 데이터의 관계 분석 및 통계적 분석을 통해 예측
모델 기반 학습
: 최적의 '모델 파라미터'를 찾는 과정
모델 파라미터를 찾는 과정이 학습의 과정
가장 잘 맞는 직선의 방정식을 찾는다 -> 최적의 기울기와 절편을 찾는다. (모델 파라미터)
무게가 음수? -> 보다 더 정확한 예측을 위해 직선식에서 곡선식으로 변형한 다항 회귀 사용
but) 다항회귀에서도 현재 아직까지 과소 적합 상태 (test가 더 높다.)
지금까지 상황 - 무게 예측이 향상되고 있다.
K-최근접 이웃 회귀 : 1033.33 (문제 : 훈련 샘플의 범위 제약 및 큰 오차)
선형 회귀 : 1241.83 (문제 : 음수값, 여전히 낮은 테스트 점수)
다항 회귀 : 1573.98 (문제 : 여전히 과소 적합 상태) -> 추가 개선 필요
3-3 특성 공학과 다항 회귀 규제
최근접 이웃 회귀
선형 회귀 (직선)
다항 선형 회귀 (곡선)
까지 학습
다중 회귀 (multiple regression)
: 여러 개의 특성을 사용하는 회귀 (높이, 두께 등)
길이 이외, 높이, 두께 등의 정보를 사용하여 무게를 예측

특성 공학 (feature engineering)
: 기존의 특성을 사용하여 새로운 특성을 뽑아 내는 작업
e.g) 3개의 특성(다중회귀)를 사용하고, 각 특성의 제곱항(다항회귀)을 활용한다.
우리가 직접 특성을 추가할 수 있지만, 사이킷런에서 이와 같은 기능 제공 도구 존재
머신러닝은 특성 공학이 중요 (데이터가 적어 좋은 특성을 판별해야한다-> 정교한 예측식 필요)
딥러닝은 특성 공학에 상대적으로 덜 영향 받음 (데이터가 많기 때문)
오히려 학습효율을 높이기 위해 차원 축소(비지도 학습) 등을 통해 특성을 줄이려고 함
판다스로 데이터 준비
판다스 : 파이썬 과학용 데이터 분석 라이브러리
다양한 데이터 준비 방법들
- 파이썬 리스트를 사용한 데이터 : zip()
- 넘파이 배열을 이용한 데이터 : colsumn_stack()
- 판다스를 사용한 데이터 : DataFrame (판다스 데이터 구조)


길이, 높이, 두께 -> 3개의 입력 특성 활용
그 외, 소스 코드 작업
타겟 데이터(무게)는 기존 넘파이 활용하여 준비
훈련 세트와 테스트 세트 구분

넘파이 튜토리얼: http://ml-ko.kr/homl2/tools_numpy.html
판다스 튜토리얼: http://ml-ko.kr/homl2/tools_pandas.html
다항 특성 만들기
- 변환기 (transformer) : 특성을 만들거나 전처리하기 위한 클래스를 변환기라 함
- 추정기 (estimator) : linear regressor, K-neighbor 등의 사이킷런의 모델 클래스(학습을 하기 위해 사용하는 클래스)
사이킷런에서 추정기는 모델 클래스에 관계없이,
일관된 API의 fit(), score(), predict() 메소드가 있다.
변환기 클래스도 일관된 fit(), transform() 메소드 제공
- fit() : 변환을 준비하기 위한 사전 변환 분석 작업
- transform() : 실제 변환하는 작업
(변환기에는 predictor/score 없음)
다항 특성을 신규로 만들기 위한 변환기를 사용하자.
특성 변환기의 fit/transform 함수
: fit() : 특성 조합 찾기, transform() : 실제 데이터로 변환

-> 변환기를 통한 특성 생성의 간단한 예제 (학습코드와 상관 X)
PolynimialFeatures : 우리가 사용할 변환기(transformer)
poly.fit( [2, 3] ) : 2와 3의 특성의 조합 찾기 (2의 제곱, 3의 제곱)
poly.transform() : 실제 조합한 특성의 데이터로 변환
결과 제일 앞의 1은 절편의 개념 (ax + b이면 b도 1곱하기 b)
PolynimialFeatures (include_bias = False) 옵션 사용시 1 제외
LinearRegression

-> fit - transform - transform 형태의 코드
-> (42, 9)로 42개의 샘플에 대해 특성이 9개로 늘어났구나를 알 수 있다. -> 다중 다항 회귀
get_feature_names_out() : 특성 종류 확인 함수
get_feature_names에서 get_feature_names_out으로 변경됨
다중 다항 회귀 모델 훈련

-> 훈련 세트 점수가 더 높게 나옴
즉, 테스트 점수가 이전값(0.977) 보다 더 높게 나오진 않았지만 (0.970 -> 0977)
과소 적합 문제는 어느정도 해결
더 많은 특성 만들기
특성 공학으로 특성을 증가시키니 성능 향상 (다중 특성, 다중 특성의 다항화)
5제곱항(degree = 5)까지 가지는 특성 모델을 구현해보자
-> 더 복잡한(정교한) 모델 만들기
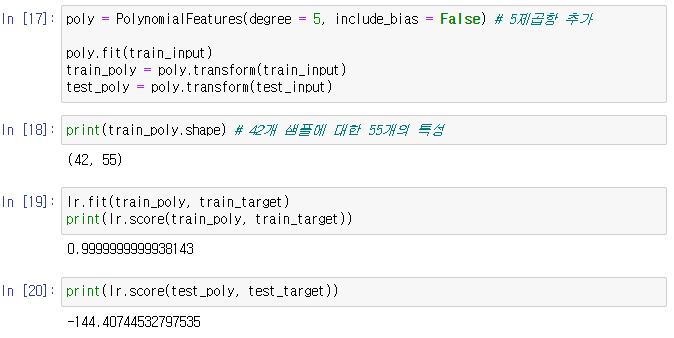
-> 42개의 샘플로 55개의 특성 생성 -> 훈련세트 수 보다 특성 수 가 더 많다.
-> 훈련 세트는 99.99% 지만 과대 적합
훈련 세트에 너무 과대 적합되어 테스트 세트는 하나도 못맞추었음
심지어 샘플 개수가 특성 개수 보다 많음
-> 규제 필요 - 단순하게 만들어야한다!
: 샘플 oriented 된 과대 적합의 완화
그래프의 정교한 기울기를 완화
규제란?
훈련세트에 너무 과도하게 학습하지 못하도록 훼방하는 것(벌칙, 규제)
기울기를 완화하는 역할 (specific -> general 일반화)
규제의 종류 : 릿지/ 랏소 기법 (L1규제와 L2규제가 있다.)

-> 새로운 x는 회귀식 above로 보이지만 학습결과식으로는 현재 below임
규제를 통한 과대적합 해소
앞서 살펴본 바와 같은 과대 적합을 줄이는 또 다른 방법 : 규제
(기존 : 이웃 개수 조정 ↑ (KNN), 모델 단순화 등)
특성의 스케일이 정규화되지 않으면 학습에 미치는 영향력이 달라짐
분류에서는 표준점수를 활용하여 스케일을 통일 시킴
하지만, 회귀(Linear regression)는 특성 스케일에 영향을 받지 않는 알고리즘
즉, 스케일에 대해 표준화 과정이 필요 없음 (관계성만 보기 때문) -> 일반적인 회귀는 모두 해당
하지만, 규제 적용시에는 회귀 문제에도 스케일을 정규화하는 과정을 거쳐야함.
특성의 스케일이 비슷해야 기울기의 가중치/ 규제(벌칙)의 영향도가 비슷해짐
규제 적용 전 정규화를 통해 스케일 조정을 해야함.
규제 전에 표준화
기존에 우리는 분류 문제에서 표준점수(z)를 통한 스케일링(평균과 표준편차)을 수행함
여기서는 사이킷런에서 제공하는 변환기의 일종인 StandardScaler()를 활용해 보자
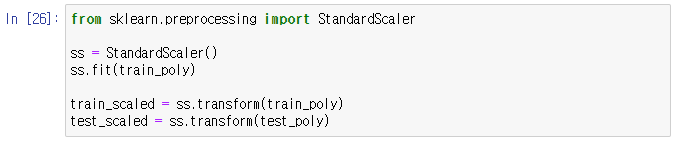
-> StandardScaler() : 특성을 표준 점수로 자동 변환해주는 변환기 클래스 (변환기의 또 다른 사례)
ss.fit(train_poly) : 훈련세트에 적용한 객체를 사용하여 테스트 세트에 적용
ss.transform() : 표준 점수로 변환된 훈련/ 테스트 세트
-> 표준 점수로 변환한 train_scaled와 test_scaled가 준비됨
이와 같은 정규화(표준화) 후 , 규제 사용
릿지(Ridge) 회귀
(규제 1) 릿지(Ridge) 회귀
가중치의 제곱(L2 Norm)을 벌칙으로 사용, L2 규제
선형 회귀에서 L2 규제 : 릿지 규제
Ridge 객체 선언
alpha = 1 (하이퍼파라미터) : 규제 강도 조절 매개변수
큰 값 : 높은 강도의 규제 적용
(가중치(Wi, 계수값)을 더 많이 줄임 (완만하게 일반화))

-> 입력은 스케일된 것, 타겟은 원래값 그대로 사용
-> 규제 모델을 통한 과대 적합 해소 및 테스트 세트 결과 향상
Norm(노름) 이란?
- 벡터의 길이 혹은 크기를 측정하는 방법
- L1 norm : 단순한 거리의 절대값의 합 (맨하탄 거리)
- L2 norm : 거리의 절대값의 합에 루트 적용
적절한 규제 강도 찾기
적절한 alpha 값을 어떻게 찾을까?
최적의 하이퍼파라미터 alpha 값 탐색 과정 -> alpha 값의 변화에 따른 결정계수(R^2) 값 탐색

-> 훈련 세트 결과 그래프
-> -3은 규제가 0.001 이라 규제가 약한 상황
훈련세트와 테스트 세트 지점 차이가 최소일 때가 제일 좋은 지점
-> 10의 -1승 즉, 규제가 0.1이 가장 좋은 지점
alpha를 0.1로 해보기

-> alpha 기본값 1일때 보다 조금 더 좋은 상황
라쏘 회귀
(규제 2) 라쏘(Lasso) 회귀
가중치의 절대값( L1 norm)을 벌칙으로 사용, L1 규제
Lasso 객체 선언
alpha = 1 (하이퍼파라미터) : 규제 강도 조절 매개변수
큰 값 : 높은 강도의 규제 적용
(가중치(Wi, 계수값)을 더 많이 줄임 (완만하게 일반화))


과소 적합 지점 -> 규제가 너무 강해 학습이 제대로 이루어지지 않아 다시 과소 적합화 됨
alpha를 10으로 해보기

-> alpha를 10으로 하니 조금 더 줄어든다.
라쏘 회귀는 특성의 가중치를 0으로 만들 수 있음 (= 특정한 특성을 없앨 수 있다.)
특성 55개 중, 가중치가 0인 것, 즉, 계수가 0 나온게 40개
유용한 특성을 골라내는 용도로 사용 (Feature selection)
릿지는 계수가 점점 커지는걸 단순하게 만들어가지만 0으로 만들 수는 없다.
라쏘는 항을 아예 없애버릴 수 있다.
규제 선형 모델
기존의 비용함수의 목표는 비용함수의 오차값 최소화 였지만
학습데이터 잔차 오류 최소화를 하고 싶다.

-> 학습데이터 잔차 오류 최소화
회귀 계수 크기 제어 : 값들이 어느정도 이상 커지지 않아야한다.

alpha = 0
: 기존 선형회귀 방식과 동일, RSS(W) 만 최소화 시킴, W에 대한 고려 X
W가 커져도 신경쓰지 않겠다는 의미
alpha = 100 or 무한대?
: 두번째 항이 커짐, 전체 식의 최소화를 위해 w를 0에 가깝게 최소화 해야한다.<- 패널티 효과
회귀 계수값을 줄이는 방법? 제곱(릿지) 혹은 절대값(라쏘)로 패널티 부여
alpha가 무한대? 모든 가중치가 0에 근접, 데이터의 평균을 지나는 직선(일반화, 단순화)


사진 출처 : 혼자 공부하는 머신러닝 + 딥러닝 강의자료
'파이썬 & 머신러닝과 딥러닝' 카테고리의 다른 글
| 14일차 - 경사하강, 결정트리, 앙상블 학습, 랜덤 포레스트, 교차검증과 그리드 서치 (1) | 2024.01.30 |
|---|---|
| 13일차 - 로지스틱 회귀, 딥러닝을 위한 기초수학, 선형 회귀, 경사하강, 다중 선형 회귀 (2) | 2024.01.29 |
| 11일차 - 머신러닝과 딥러닝의 기본 원리, 훈련세트와 테스트세트, 데이터 전처리 (1) | 2024.01.25 |
| 10일차 - 웹스크래핑 기법 학습 및 이를 기반으로 한 미니프로젝트 수행 (0) | 2024.01.17 |
| 9일차 - 서울시 CCTV 현황, 인구현황, 범죄현황을 기반으로 데이터 분석 실습 (0) | 2024.01.16 |



