4-1 로지스틱 회귀
로지스틱 회귀는 분류다.
지금까지 분류 문제, 회귀 문제, 데이터 전처리, 특성 조합 등을 학습
이제는 무슨 생선이 있을지 확률을 주고 럭키백을 구매하도록 하자.
도미와 빙어의 확률 문제 : 분류 문제이면서 확률을 함께 제공
( 분류 문제는 확률과 관계가 있다.)
(확률 50%를 기준으로 분류 작업 수행)
확률 계산하기
k-최근접 이웃 분류기? 다수결로 결정
여기서 확률이란?
이웃 클래스의 비율(개수)을 확률로 출력
k-최근접 이웃 분류기를 활용하여 각 종류의 확률을 계산해보자
데이터 준비
판다스 데이터 프레임을 이용한 데이터 준비
-> 2차원 표 형식의 주요 데이터 구조
(장점 : 넘파이로 변환이 용이, 사이킷런과 호환)

-> 입력데이터( = 특성데이터), 2D List 형태 (2차원) - 5개의 특성을 활용한 다중회귀
-> 타겟 데이터 1D List (1차원)
k-최근접 이웃의 다중 분류
다중 분류? 타겟이 3개 이상의 클래스가 포함된 문제
훈련세트와 테스트 세트 구분
표준화 전처리(스케일링) <- 분류 문제

-> fit : 표준편차, 분산의 관계 파악
-> transform : 실제 값 반환
(다항 특성 만들기 3-3에서는 fit : 특성 조합 찾기)
k-최근접 이웃 분류기의 확률 예측

-> 현재 7진 분류를 하려고 하고 있다.
-> 5개의 생선에 대해 예측을 해보고 prediction 결과를 보여준다.
-> _속성 : 모델이 데이터로 학습한 내용을 저장하는 속성
-> predict_proba() : 확률을 예측하게 하는 함수
-> kn.kneighbors : 이웃의 인덱스와 거리 확인
predict proba() 출력의 이해 : 각 클래스별 확률값 반환
-> 결과만 보고싶어 한 번 더 가공
이웃을 3개로 하면 가능한 확률 조합이 33, 66, 100% 3가지뿐
-> 좀 더 합리적인 확률을 제공하면서 생선을 분류하자 -> 로지스틱 회귀
로지스틱 회귀를 사용한 분류 : 이진 분류, 다중 분류
로지스틱 회귀
대표적인 분류 알고리즘
선형회귀와 동일하게 선형 함수식을 찾음
이 때, 선형 함수식의 결과 값인 z는 아주 큰 음수이면 0, 아주 큰 양수이면 1로 출력
-> 이를 가능하게 하는 함수 : 시그모이드 함수
즉, 선형 함수의 결과 값을 시그모이드 함수에 대입하여 출력 확인
그 출력된 그래프가 확률 그 자체


-> 올라가는 기울기와 포인트가 달라진다.
-> x가 커지면 1에 수렴, x가 작아지면 0에 수렴
ax+b 에서 a가 커질 수록 기울기가 가파른 모습 이걸 확률로 씀
로지스틱 회귀는 시그모이드 함수를 사용하여 회귀를 사용해 분류를 푼다
시그모이드 함수가 보여주는 그래프 그 자체가 확률
(a가 커질수록 오차는 작아지지만, 커진다고 해서 오차가 없어지진 않는다.)
회귀는 선식이 어떻게 생긴지 학습하는 것,
e의 지수 식 그래프를 보고 학습하는 시그모이드 선식에 따라 확률이 달라짐
시그모이드 함수 (= 로지스틱 함수)
z값에 따라 0~1 사이의 값이 확률로 변환되어 출력
- 출력(파이)이 0.5 이상이면 양성 클래스, 0.5 이하이면 음성 클래스 (출력 값 사용(predict_proba()))
- 입력(z)이 양수면 양성 클래스, 음수면 음성 클래스 (입력 값 사용(기존의 predict()))
시그모이드 함수

-> 시그모이드 함수 구현 및 그래프 확인
-> predict_proba() : 실제 그 출력값을 확률값으로 사용하고 0.5 기준으로 분류 기준으로 활용
로지스틱 회귀 (이진 분류)

-> 양성일 확률이 출력 됨
알파벳 순서로 Bream(도미, 0, 음성 클래스), Smelt(빙어, 1, 양성 클래스)
-> 'Bream', 'Smelt'가 true인 인덱스만 뽑아내기 -> Boolean Indexing
-> 학습하는 방법은 선형회귀, 로지스틱 회귀 모두 LogisticRegression
-> 출력으로 판단을 하자. 이 확률값을 럭키백에 쓰기
로지스틱 회귀 식(계수, 절편) 확인
회귀에서의 학습 식 : 새로운 입력값에 대한 결과값 유추용
여기서 수행하는 분류(로지스틱 회귀)에서의 학습식 : 분류를 위한 공간 분할용
-> (실제 작동) 시그모이드 함수에 대입하는 입력값 계산용

-> 이 긴 z를 e의 지수승에 넣었다.
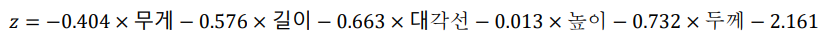
-> 학습 결과 도출된 함수

-> 입력으로 표준 점수 z값을 시그모이드 함수 expit() 에 입력 -> 확률을 얻자 -> 그 확률로 분류하자
해당 기능을 제공(입력: z, )
-> decision_function() : 입력에 대한 표준점수 z값을 출력해주는 함수
-> 결과 -6 : 매우 bream, 양수 : smelt

-> expit() : 파이썬 싸이파이 라이브러리에서 제공하는 시그모이드 함수의 출력 값인 확률 제공
-> 결과 y축에 어디에 매핑된지 보여줌 (양성일 확률)
(결론은 복잡하게 생각하지 말고 predict_proba() 함수를 활용하면 된다.)

특성 5개에 대한 가중치(계수) 5개 + 절편 1개
도미와 빙어의 이진 분류를 위한 학습 결과 도출된 학습식
-> 빙어를 찾아내는 학습식 (큰 값이 나오면 빙어 아니면 다 도미) -> 이진분류
-> n진 분류를 학습하기 위해서는 분류 클래스 만큼 n개의 학습식 학습
(정리)
각 샘플의 5개 특성(무게, 길이,,, 두께) 을 이 함수식에 대입
계산 결과 출력(z)
분류 문제이므로 스케일링, 즉, 해당 결과를 표준 점수로 변환 decision_function
이 함수를 시그모이드 함수에 대입하여 0~1 사이 값 획득(== 확률값) expit()
확률값을 기반으로 이진 분류 수행 predict_proba()
로지스틱 회귀 오차 구하기, 오차 줄이기
logh와 편미분을 위한 a, b와의 관계성?

MSE : 예측값에서 실제값과의 차이의 제곱을 통해 오차를 구하고 이를 평균함,
그 오차값에 a/b가 포함되어 있음
즉, MSE에서 yhat에 a와 b가 포함된 예측값이고
이 예측값을 실제 y값과 비교하여 그 차이를 줄여야함
로지스틱회귀에서는
주어진 오차함수 수식에서
y 혹은 1-y항은 1 혹은 0으로 상수 개념이며,
“h”는 예측값이고 “logh”가 바로 줄여야 되는 오차값 임
h인 예측값은 선식의 결과값, 즉 로지스틱회귀에서는 시그모이드 함수
h=1/(1+e의 –(ax+b)승)로 계산된 결과값) -> 결국 a, b가 포함됨

-> 시그모이드 예측값 h를 오차값 로그에 대입
시그모이드 함수가 분류에 쓰이고 오차함수에서는 로그가 쓰임
이 둘을 같이 쓰고 로그 함수 출력 결과에 예측값을 대입해서 편미분

-> 기울기와 절편의 최저값을 찾아가는 것이 경사하강
Logistic_regression
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
#공부시간 X와 성적 Y의 리스트를 만들기
data = [[2, 0], [4, 0], [6, 0], [8, 1], [10, 1], [12, 1], [14, 1]]
x_data = [i[0] for i in data]
y_data = [i[1] for i in data]
#그래프로 나타내기
plt.scatter(x_data, y_data)
plt.xlim(0, 15)
plt.ylim(-.1, 1.1)
# 기울기 a와 절편 b의 값을 초기화
a = 0
b = 0
# 학습률 정하기
lr = 0.05
# 시그모이드 함수 정의
def sigmoid(x):
return 1 / (1 + np.e ** (-x))
# 경사 하강법을 실행
for i in range(2001):
for x_data, y_data in data:
a_diff = x_data * (sigmoid(a * x_data + b) - y_data)
b_diff = sigmoid(a * x_data + b) - y_data
a = a - lr * a_diff
b = b - lr * b_diff
if i % 1000 == 0: # 1000번 반복될 때마다 각 x_data값에 대한 현재 a, b값 출력
print("epoch=%.f, 기울기=%.04f, 절편=%.04f" % (i, a, b))
# 앞서 구한 기울기와 절편을 이용해 그래프 그리기
plt.scatter(x_data, y_data)
plt.xlim(0, 15)
plt.ylim(-.1, 1.1)
x_range = (np.arange(0, 15, 0.1)) # 그래프로 나타낼 x값의 범위 정하기
plt.plot(np.arange(0, 15, 0.1), np.array([sigmoid(a*x + b) for x in x_range]))
로지스틱 회귀(다중 분류)
이제, 7개의 생선 전체에 대한 다중 분류해보기
로지스틱 회귀는 기본적으로 L2(릿지) 규제
규제 매개변수 이름 : c (기본값 1) // alpha 대신 사용
사이킷런 분류 모델의 규제 강도 : c 값을 조정
(c 값이 클수록 규제가 약해짐)
로지스틱 회귀는 기본적으로 반복 학습을 시행
max_iter= 1000 : 반복 횟수 (반복 학습) max_iter 정의
(딥러닝에서 epoch와 비슷한 개념)

-> 분류 모델임 따라서 정확도(%) 출력 -> 93은 좀 작아보여 과소 적합
(회귀모델의 score 값은 결정계수)

-> 첫줄에서 0.0841이 가장 높으니 이거다라고 알 수 있음
-> coef(계수) : (7,5) : 7개의 클래스(선형식)에 각각 5개의 계수
-> (7, ) : 7개의 각 클래스별 식의 절편
소프트맥스 함수의 원리
-> 7개의 클래스 : 각 클래스마다 하나의 선형식 학습
-> 각 샘플(5개의 특성)을 학습한 선형식 7개에 각각 대입해서 출력값 z값 각각 계산
-> 이를 각각 시그모이드 함수에 대입하여 7가지 결과 중 가장 큰 출력을 가지는 클래스가 예측 클래스로 결정
-> 이를 알려주는게 소프트맥스 함수
소프트맥스 함수
: 7개의 클래스(다중분류)를 각각 0~1 사이의 확률로 표시하는 함수
시그모이드 함수: 이진분류
소프트맥스 함수 : 다중분류
각 샘플에 대한 7개의 표준점수로 변환된 z값 출력

-> 표준 점수 함수 출력
확률 분포 합을 100을 기준으로 표시 -> 소프트맥스 함수 softmax()

-> axis = 1 : 행이 0, 열이 1 -> 열을 바꾸어가며 특정 행의 통계값 계산
-> 7개의 생선에 대해 럭키백을 만들었다.
(앞 슬라이드의 predict_proba()의 결과인 proba 배열과 일치)
로지스틱 회귀를 사용한 분류 및 확률 계산
선형 함수 학습 후, 이를 시그모이드/소프트맥스 함수를 통과하여 확률 구함
이진분류에서는 시그모이드 결과값을 바로 확률값으로 사용 가능
소프트맥스 함수를 사용한 다중 분류란?
7개의 물고기 클래스의 구분을 위한 7개의 함수식 학습
각 해당식을 z1~z7이라 하자
각 샘플의 특성값을 7개의 식에 각각 대입
그 결과를 각각 시그모이드 함수에 대입 : 각 클래스별 시그모이드값 획득
그리고, 이들의 시그모이드 함수 대입의 총 합을 e_sum이라 하자

(정리)
로지스틱 회귀의 분류 확률 계산
: 이진/다중 분류를 위한 선형 함수식 1개 혹은 n개를 학습 후,
입력데이터를 표준점수 z로 변환한 뒤,
이를 시그모이드 함수(expit()) 혹은 소프트맥스(xoftmax())의 입력값으로 통과 시킴
-> 그 결과가 분류를 위한 확률값
확률값 계산은
이진 분류는 학습 방정식의 결과(z)를 시그모이드 함수에 대입, 0~1사이의 값을 확률로 그대로 사용
다중 분류에서는 클래스별 z 값에 대한 시그모이드 결과를 계산하고 이들의 합산 후 자기 클래스 비율로 확률 계산
즉, 각 클래스별로 회귀 모델이 학습한 방정식이 각각 존재 (Zi= a * weight + b * length + ...)
따라서, 클래스 i마다 Z값이 존재하며, 각 클래스별로 Z 값을 계산하여
가장 높은 Z값을 출력하는 클래스를 예측 클래스로 선정
분류와 해당 분류의 확률을 함께 제공할 경우,
predict_proba( ) 함수 결과값 사용 내부적으로는 입력 데이터 각각을 표준점수(decision_function( ))로 변환한 뒤,
이를 분류 함수 (이진의 경우 expit( ), 다중의 경우 softmax( ))에 입력
-> 이진이든 다중이든 모두 predict_proba( ) 함수와 결과가 일치함을 확인
딥러닝을 위한 기초수학
편미분
: 여러가지 변수가 식 안에 있을 때 우리가 원하는 변수 하나만 미분 그 외엔 모두 상수로 취급

편미분이 가지는 의의

-> y가 변할 때 x가 영향력을 줬다.
-> 영향력의 크기 비교가 아닌 관계를 알 수 있다.
ex) 체중 함수가 체중(야식, 운동) 처럼 야식/ 운동에 영향을 받는 2변수 함수라 가정시
편미분을 이용하면 각 변수 변화에 따른 체중 변화량을 구할 수 있다.
-> 영향력간의 관계를 알 수 있다
-> 각각의 특성에 대해 편미분하여 계수를 구하면
지수와 지수 함수
시그모이드 함수 : 지수 함수에서 밑의 값이 자연 상수 e인 함수를 말함
로그와 로그 함수

x축에 대하여 대칭 이동 + x,y축으로 대칭 후, x축으로 1 평행 이동하면

-> 오차 함수로 쓰이는 로그함수
2차함수가 머신러닝에서 중요하고 접근하기 위해 편미분이 필요
위 두 로그함수의 합을 오차값 계산을 위해 사용

-> y_data가 1이면 B가 없어짐, 0이면 A가 없어짐
-> 로지스틱 회귀에서 사용하는 오차를 교차 엔트로피 오차라 함
선형 회귀
선형 회귀 : 독립 변수 x를 사용해 종속 변수 y의 움직임을 예측하고 설명하는 작업
단순 선형 회귀(simple linear regression) : 하나의 x 값 만으로도 y 값을 설명할 수 있을 때
다중 선형 회귀(multiple linear regression) : x 값에 해당하는 요소가 여러 개 (x, y, z…) 필요할 때
최소 제곱법 (Least Squares, LS)
: 오차가 가장 작은, 주어진 좌표의 특성을 가장 잘 나타내는 직선 (원하는 예측 직선)
기존 데이터를 가지고, 어떤 선이 그려질지 예측한 뒤,
답이 나오지 않은 무언 가를 그 선에 대입하여 예측값을 구함
최소 제곱법 공식을 알고 적용하면,
일차 함수의 기울기 a와 y 절편 b 를 바로 구할 수 있다. -> 오차를 최소화하는 직선 구하기 가능
경사 하강 : 오차 줄이기
: 먼저 오차를 구한 다음, 오차가 작은 쪽으로 이동시키는 방법
각 선의 오차를 계산할 수 있어야 하고 (오차(실제값과 예측값의 차이) 구하기),
오차가 작은 쪽으로 바꾸는 알고리즘이 필요(오차 줄이기)
최소 제곱법으로 회귀 직선을 구하기
x와 y의 평균값, 기울기 공식의 분모와 분자, 기울기와 y 절편 구하기
Least_Square_Method
import numpy as np
# x 값과 y값
x = [2, 4, 6, 8]
y = [81, 93, 91, 97]
# x와 y의 평균값
mx = np.mean(x)
my = np.mean(y)
print("x의 평균값 : " , mx)
print("y의 평균값 : " , my)
# 기울기 공식의 분모
divisor = sum([(mx - i) ** 2 for i in x])
# 기울기 공식의 분자
def top(x, mx, y, my):
d = 0
for i in range(len(x)):
d += (x[i] - mx) * (y[i] - my)
return d
dividend = top(x, mx, y, my)
print("분모 : ", divisor)
print("분자 : ", dividend)
# 기울기와 y 절편 구하기
a = dividend / divisor
b = my - (mx * a)
# 출력으로 확인
print("기울기 a = ", a)
print("y 절편 b = ", b)

평균 제곱 오차 (Mean Square Error, MSE) 구하기
오차를 확인해서 오차가 줄어드는 쪽으로 식을 변경해야함
오차를 확인하기 : 오차 함수, 오차를 줄이기 : 경사 하강
이를 위해 주어진 선의 오차를 평가하는 오차 평가(확인) 알고리즘이 필요
오차 평가 알고리즘의 대표적 사례 : 평균 제곱 오차(MSE)
경사하강 : 가설을 세운 뒤에 일단 그리고 오차를 조금씩 수정해나가자
1. 최소 제곱법으로 회귀 직선을 구했음
2. 임의의 직선을 그린 다음 평균 제곱 오차방법으로 오차값 확인
3. 줄어드는 방향으로 수정하고 오차를 수정
오차 = 예측 값 - 실제 값
각각의 오차를 하나의 값으로 만들어야함
오차의 합을 구할 때는 각 오차(예측값-실제값)의 값을 제곱해주기


평균 제곱 오차(Mean Squared Error, MSE)
: 오차의 합을 n으로 나누면 오차 합의 평균을 구할 수 있음

MSE : 예측값과 실제값의 차이의 제곱의 합
분산 : 특정 값과 평균의 차이의 제곱의 합
Mean_Squared_Error
import numpy as np
# 가상의 기울기 a와 y 절편 b를 정하기
fake_a=3
fake_b=76
# 공부 시간 x와 성적 y의 넘파이 배열 만들기
x = np.array([2, 4, 6, 8])
y = np.array([81, 93, 91, 97])
# 평균 제곱 오차 구하기
# y=ax + b에 가상의 a,b 값을 대입한 결과를 출력하는 함수
def predict(x):
return fake_a * x + fake_b
# 예측 값이 들어갈 빈 리스트 만들기
predict_result = []
# 모든 x 값을 한 번씩 대입하여 predict_result 리스트를 완성하기
for i in range(len(x)):
predict_result.append(predict(x[i]))
print("공부시간=%.f, 실제점수=%.f, 예측점수=%.f" % (x[i], y[i], predict(x[i])))
# 평균 제곱 오차 함수를 각 y 값에 대입하여 최종 값을 구하는 함수
n=len(x)
def mse(y, y_pred):
return (1/n) * sum((y - y_pred)**2)
# 평균 제곱 오차 값을 출력
print("평균 제곱 오차: " + str(mse(y,predict_result)))
오차 수정하기 : 경사 하강법
기울기와 절편의 최저값을 찾아가는 것이 경사하강
미분 계수의 값이 양수면 음의 방향으로 이동,
미분 계수의 값이 음수면 양의 방향으로 이동
우리가 찾는 최솟값 m에서의 순간 기울기임를 보면
그래프가 이차 함수이므로 꼭짓점의 기울기는 x축과 평행한 선이 됨. 즉, 기울기가 0임
-> 미분 값(순간 기울기)이 0인 지점 찾기
경사 하강법
: 가중치를 주면 미분계수 만큼 a를 업데이트 하면 기울기가 0인 한 점(m)으로 수렴
(학습률을 너무 크게 잡아서
기울기의 부호를 바꿔 이동시킬 때 적절한 거리를 찾지 못해 너무 멀리 이동시 키면
a값이 한 점으로 모이지 않고 위로 치솟아 버림 )

학습률 (Learning Rate)
: 이동 거리를 정해준다.(= 순간 변화율의 반영 정도를 조정해줌) -> 학습률을 곱해 값을 업데이트
새로운 기울기 = 이전 기울기 – 학습률 * 새로운 지점의 기울기(미분 계수)
( - 가 음수면 양의 방향으로 이동한단 말)
평균제곱오차 식을 통해 오차함수의 이차 함수 도출
평균제곱 오차식에

를 대입하면
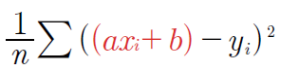
-> a, b에 대한 제곱항 발생 (이차 곡선 생성)
a도 이차항이 나오고 b도 이차항이 나오니
오차 함수식을 a에 대해서 편미분하고 b에 대해서 편미분


미분 결과에 학습률을 곱한 후 기존 a값을 업데이트
a 값(즉, a의 위치)은 m 위치를 기준으로 커지기도 하고 작아지기도 함
즉, adiff가 (+)면 a 감소, adiff가 (-)면 a 증가, 계산된 adiff 기울기의 1r(%) 비율만큼만 반영하겠다는 것
Linear_Regression
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 공부시간 X와 성적 Y의 리스트를 만들기
data = [[2, 81], [4, 93], [6, 91], [8, 97]]
x = [i[0] for i in data]
y = [i[1] for i in data]
# 그래프로 표현
plt.figure(figsize=(8,5))
plt.scatter(x, y)
plt.show()
# 리스트로 되어 있는 x와 y값을 넘파이 배열러 바꿔주기
# 인덱스를 주어 하나씩 불러와 계산이 가능해지도록 하기 위함
x_data = np.array(x)
y_data = np.array(y)
# 기울기 a와 절편 b의 값을 초기화
a = 0
b = 0
# 학습률을 정하기
lr = 0.03
# 몇 번 반복될 지 설정
epochs = 2001
# 경사하강법
for i in range(epochs):
y_hat = a * x_data + b # epoch 수 만큼 반복
error = y_data - y_hat # 오차 구하기
a_diff = -(2/len(x_data)) * sum(x_data * (error)) # 오차함수를 a로 미분한 값
b_diff = -(2/len(x_data)) * sum(error) # 오차함수를 b로 미분한 값
a = a - lr * a_diff # 학습률을 곱해 기존의 a값 업데이트
b = b - lr * b_diff # 학습률을 곱해 기존의 b값 업데이트
if i % 100 == 0: # 100번 반복될 때마다 현재의 a, b값 출력
print("epoch=%.f, 기울기=%.04f, 절편=%.04f" % (i, a, b))
# 앞서 구한 기울기와 절편을 이용해 그래프 그리기
y_pred = a * x_data + b
plt.scatter(x, y)
plt.plot([min(x_data), max(x_data)], [min(y_pred), max(y_pred)])
plt.show()
-> 평균제곱오차와 경사하강법을 다 적용해 보았을 때 결과 일치
다중 선형 회귀
x, y 두개의 축의 선 상에서 흩어져있는게 x1, x2, y 3개의 축으로 3차원 면식에서 흩어짐
-> 더 많은 데이터 필요
평균제곱 오차식 = 1/n * sum[ {(a1 x 1 + a2 x 2 + b) - y} ** 2]
이 식에 대해 a1/a2/b에 대해 각각 편미분
텐서플로에서 실행하는 선형회귀, 다중 선형 회귀 모델
Multi-Linear-Regression
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
#공부시간 X와 성적 Y의 리스트를 만듭니다.
data = [[2, 0, 81], [4, 4, 93], [6, 2, 91], [8, 3, 97]]
x1 = [i[0] for i in data]
x2 = [i[1] for i in data]
y = [i[2] for i in data]
#그래프로 확인해 봅니다.
ax = plt.axes(projection='3d')
ax.set_xlabel('study_hours')
ax.set_ylabel('private_class')
ax.set_zlabel('Score')
ax.dist = 11
ax.scatter(x1, x2, y)
plt.show()
#리스트로 되어 있는 x와 y값을 넘파이 배열로 바꾸어 줍니다.(인덱스를 주어 하나씩 불러와 계산이 가능해 지도록 하기 위함입니다.)
x1_data = np.array(x1)
x2_data = np.array(x2)
y_data = np.array(y)
# 기울기 a와 절편 b의 값을 초기화 합니다.
a1 = 0
a2 = 0
b = 0
#학습률을 정합니다.
lr = 0.05
#몇 번 반복될지를 설정합니다.(0부터 세므로 원하는 반복 횟수에 +1을 해 주어야 합니다.)
epochs = 2001
#경사 하강법을 시작합니다.
for i in range(epochs): # epoch 수 만큼 반복
y_pred = a1 * x1_data + a2 * x2_data + b #y를 구하는 식을 세웁니다
error = y_data - y_pred #오차를 구하는 식입니다.
a1_diff = -(1/len(x1_data)) * sum(x1_data * (error)) # 오차함수를 a1로 미분한 값입니다.
a2_diff = -(1/len(x2_data)) * sum(x2_data * (error)) # 오차함수를 a2로 미분한 값입니다.
b_new = -(1/len(x1_data)) * sum(y_data - y_pred) # 오차함수를 b로 미분한 값입니다.
a1 = a1 - lr * a1_diff # 학습률을 곱해 기존의 a1값을 업데이트합니다.
a2 = a2 - lr * a2_diff # 학습률을 곱해 기존의 a2값을 업데이트합니다.
b = b - lr * b_new # 학습률을 곱해 기존의 b값을 업데이트합니다.
if i % 100 == 0: # 100번 반복될 때마다 현재의 a1, a2, b값을 출력합니다.
print("epoch=%.f, 기울기1=%.04f, 기울기2=%.04f, 절편=%.04f" % (i, a1, a2, b))
#참고 자료, 다중 선형회귀 '예측 평면' 3D로 보기
import statsmodels.api as statm
import statsmodels.formula.api as statfa
#from matplotlib.pyplot import figure
X = [i[0:2] for i in data]
y = [i[2] for i in data]
X_1=statm.add_constant(X)
results=statm.OLS(y,X_1).fit()
hour_class=pd.DataFrame(X,columns=['study_hours','private_class'])
hour_class['Score']=pd.Series(y)
model = statfa.ols(formula='Score ~ study_hours + private_class', data=hour_class)
results_formula = model.fit()
a, b = np.meshgrid(np.linspace(hour_class.study_hours.min(),hour_class.study_hours.max(),100),
np.linspace(hour_class.private_class.min(),hour_class.private_class.max(),100))
X_ax = pd.DataFrame({'study_hours': a.ravel(), 'private_class': b.ravel()})
fittedY=results_formula.predict(exog=X_ax)
fig = plt.figure()
graph = fig.add_subplot(111, projection='3d')
graph.scatter(hour_class['study_hours'],hour_class['private_class'],hour_class['Score'],
c='blue',marker='o', alpha=1)
graph.plot_surface(a,b,fittedY.values.reshape(a.shape),
rstride=1, cstride=1, color='none', alpha=0.4)
graph.set_xlabel('study hours')
graph.set_ylabel('private class')
graph.set_zlabel('Score')
graph.dist = 11
plt.show()
사진 출처 : 혼자 공부하는 머신러닝 + 딥러닝 강의자료
'파이썬 & 머신러닝과 딥러닝' 카테고리의 다른 글
| 15일차 - 비지도 학습, 군집 알고리즘, k-평균, 차원축소, 주성분 분석 (2) | 2024.01.31 |
|---|---|
| 14일차 - 경사하강, 결정트리, 앙상블 학습, 랜덤 포레스트, 교차검증과 그리드 서치 (1) | 2024.01.30 |
| 12일차 - k-최근접 이웃 회귀, 선형회귀, 다항 회귀, 다중 분류, 특성공학, 규제 선형 모델 (0) | 2024.01.26 |
| 11일차 - 머신러닝과 딥러닝의 기본 원리, 훈련세트와 테스트세트, 데이터 전처리 (1) | 2024.01.25 |
| 10일차 - 웹스크래핑 기법 학습 및 이를 기반으로 한 미니프로젝트 수행 (0) | 2024.01.17 |



