(복습)
상자 내부의 생선 확률 예측 문제 -> K-최근접 이웃 분류 알고리즘 활용
- 가장 가까운 K개의 이웃 찾고,
- 그 클래스 개수(비율) 사용
- 확률 종류가 1/n 로만 출력 (고정 확률값)
조금 더 현실적 확률 출력
-> 로지스틱 회귀 (분류 알고리즘)
선형 방정식 학습 및 표준점수 Z값 확인
확률적 분류 문제로 변환 위해 Z 값 사용
이진 분류 : 시그모이드 함수
다중 분류 : 소프트맥스 함수
𝑧 = 𝑎 × 무게 + 𝑏 × 길이 + 𝑐 × 대각선 + 𝑑 × 높이 + 𝑒 × 두께 + 𝑓
4-2 경사하강
럭키백 대박
데이터가 동적으로 계속 갱신되고 있는 상황
어떤 생선이 회사에 추가될지, 그리고 언제 추가될지 모름
새로운 샘플이 도착할 때 마다 계속 추가적으로 훈련하는 모델이 필요함
(1) 데이터가 추가될 때 마 새로운 모델 생성해서 매번 재학습?
(2) 데이터 추가시,기존 데이터 일정량 버리고 일정량 추가 (소수 데이터 소멸 가능성?)
(3) 데이터 추가될 때마다 기존 모델 업데이트 (점진적 학습)
-> 확률적 경사하강 (샘플 하나씩 학습) - 기본 최적화 알고리즘
확률적 경사 하강법 (점진적 학습)
: 가장 가파른 경사(최대한 빨리 학습)를 조금씩 내려가는 방법(오차량 조절)
확률 == 랜덤(무작위)
확률적 경사 하강이란?
특정 머신러닝 알고리즘이 아니고, 알고리즘을 훈련(최적화)하는 방법 Optimizer (*오차 줄이기*)
- 확률적 경사 하강법 : 한개씩 꺼내기
- 미니 배치 경사 하강법 : 여러개씩 꺼내기
- 배치 경사 하강법 : 몽땅 꺼내기

10만개에 대한 데이터가 있다고 가정시 모두 보면 시간이 오래걸리니까
확률적으로 랜덤하게 한묶음만 잡아서 얘네들의 오차만 보자 -> 미니 배치 경사 하강법
30개가 한묶음이라 가정시 30개씩 랜덤으로 묶어 계속 반복
꺼낸게 조금씩 경사를 따라 이동 -> 학습률
(가장 가파른 경사를 조금씩 내려와야함, 보폭이 너무 크면 다시 올라옴)
훈련세트를 1번 다 사용 : 1에 포크
훈련세트에 샘플을 모두 채우고 다시 시작
( 훈련데이터가 모두 준비되어 있지 않더라도, 혹은 매일매일 데이터가 업데이트되어도 학습을 이어갈 수 있음 )
손실 함수
: 나쁜 정도를 측정하는 함수 (== 비용함수)
- 손실 함수 : 샘플 하나에 대한 손실 정의
- 비용 함수 : 모든 샘플에 대한 손실 함수의 합
(보통 일반적으로 혼용함)
경사(or 산)란 무엇인가?
손실함수 (loss function) 그래프
나쁜 정도를 측정하는 함수 (*오차 구하기*)
손실 함수값이 낮아 지는 방향으로 가중치와 절편을 수정
분류에서 손실이란?
정답을 못맞추고 틀린 것 (분류의 손실은 0 혹은 100)


로지스틱 손실 함수
이항 분류에서 사용되는 손실함수 -> 로지스틱 손실함수 (log)
== binary cross entropy
( 다항 분류에서의 손실함수 : categorical_crossentropy )
회귀에서 사용되는 손실함수
- MSE : 직선까지의 거리 계산, 특이치(outlier)에 민감
- MAE : 특이치에 덜 민감
- RMSE (평균 제곱근 오차) : 오류 지표를 실제 값과 유사단위로 변환, 해석 용이 (하나하나의 패턴)
- MAPE: 예측값과 실제값의 상대적인 차이를 파악하는데 유용
- (MAE : 예측 오차의 크기 파악에 유용, 크기만 파악함)
로지스틱 손실 함수는
분류 문제에서는 정확도(accuracy, %)로 성능 측정
그 후, 로지스틱 손실 함수로 오차(loss) 측정
그 후, 경사 하강으로 최적화 (오차 감소)

정답(타깃)이 0이었는데 0을 0.2로 예측, 0을 0.8로 예측
-> 0을 0.2로 예측한다는 걸 1이 0.8이라는 것으로 바꿈
-> 많이 틀리면 많은 손실을 주고싶고 적게 틀리면 적은 손실을 주고 싶다.


타겟이 1일때, 마이너스 로그 사용
가령, 0.8로 예측 : 작은 음수 (예측) -> 작은 양수 (-log)마이너스 로그)
타겟이 0일때, 대칭 및 이동 그래프 사용
가령, 0.2로 예측 : 0.8로 변환 작은 음수 (1-예측) -> 작은 양수 (-log)
손실이 작아지는 방향으로 가중치와 절편을 계속 업데이트 해 나감
이차함수와는 다르고 최적의 값이 없다 -> 0에 가까워 질 수는 있지만 0은 X -> 끊어줘야함
로지스틱 손실 함수는 로그 함수를 활용함 <- 오차 계산용
로지스틱 회귀(분류)를 위한 로지스틱 함수 (= 시그모이드 함수)와 혼동 말 것. <- 분류(확률) 계산용
(정리)
분류를 위한 로지스틱 회귀는
시그모이드(로지스틱)함수로 확률 계산 후 분류를 위한 클래스를 결정(0/1)하고
그 후, 로지스틱손실함수(== log 함수)로 오차를 측정한다.
데이터 전처리
확률적 경사하강을 이용한 분류 모델 만들기
1. 데이터 불러오기
2. 훈련세트와 테스트세트 구분
3. 데이터 전처리(스케일링)

-> 특성마다 스케일이 같아야 함.
(분류 문제는 스케일링에 유의해야 함)
경사 하강 사용시는 반드시 표준 점수로 특성의 스케일을 변환해야 함.
-> 최종적으로 train_scaled, test_scaled가 준비됨
SGDClassifier
사이킷런에서 제공하는 분류를 위한 확률적 경사하강법
(회귀 모델 : SGDRegressor )

-> loss 손실함수 종류 지정 : 로지스틱 손실 함수 (log 함수) 사용 로지스틱 회귀(분류) 모델 훈련
max_iter : 에포크 횟수
partial_fit으로 점진적 학습 해보자
이전을 유지하면서 한 번 더 학습

-> 다시 fit() 호출?
이전 학습 결과 (가중치 절편등) 모두 버리고 훈련
vs. partial_fit() 이를 유지하면서 1 에포크 추가 훈련 (partial_fit)
즉, 하나씩 샘플을 꺼내는 방식으로 샘플 전체 한번 더 학습 하기 (1 epoch)
-> 조금 향상된 결과
얼마나 partial_fit()을 반복해야하나 -> 에포크 횟수 조절
에포크와 과대/과소적합
에포크 횟수에 따라 과대/ 과소 적합 발생

-> 규제가 너무 작으면 지나친 학습 규제가 너무 크면 지나친 일반화

-> 에포크가 반복될 수록 정확도 향상
그 후, 과대적합화 됨 (테스트 세트 성능 감소)
최적의 에포크 지점까지만 설정 후, 종료해야 함
(에포크가 적을 땐 아직 학습을 덜해서 과소 적합)
확률적 경사에서 최적의 에포크 찾는 것이 중요
조기 종료
: 과대 적합이 시작하기 전에 훈련을 자동으로 멈추게 하는 것
테스트 점수가 감소하기 시작하는 위치 찾기

-> _변수 : 나중에 사용되지 않고 버리는 값 (반복 횟수 임시 저장하기 위한 용도)
-> partial_fit 의 classes=classes 옵션
: fit 없이 partial_fit을 쓸 경우는, 일부만 학습한다고 가정하기 때문에 전체 클래스가 안 나올 수도 있음
따라서 클래스 개수를 미리 지정해 주어야 함.
여기서는 전체 데이터를 다 한번씩 경사하강으로 사용하기 때문에 문제 없지만,
전체의 일부를(00%) 훈련으로 사용할 경우, 특정 클래스가 없을 수 있음

-> 300번 돌렸을 때 대략 100정도로 그래프상으로 확인 가능
최대 100 max_iter 지정 후, 다시 해 보자.

-> tol = 10은 10번 더 해보겠다는 의미
-> tol =NONE : 성능향상 최소치 지정 (none : 100번 모두 수행)
참고
손실함수로 log를 많이 쓰지만 대신 hinge 사용

-> SGDClassifier의 기본 손실 함수
SVM에서 사용되는 손실 함수
1이상으로 예측 (맞게 예측) : 오차 없음
음수로 크게 예측할 수록 오차 추가 부여
0~1 사이 예측 : 맞았으나 더욱 맞는 쪽으로 이동시키기 위해 작은 오차 부여
(복습)
확률적경사하강법
:점진적학습(랜덤,샘플하나씩)
대규모 데이터를 이용하는 딥러닝 학습에 적합
머신 러닝 모델이나 알고리즘이 아님
모델을 훈련(최적화, optimizer)하는 방법 (오차줄이기)
회귀모델 : MSE (평균제곱오차)를 손실함수로 사용
분류모델
: 정확도로 성능판단
MSE 손실함수로는 정확도를 사용 못함
-> 따라서 대안으로 로지스틱손실함수를 사용
손실함수
: 얼마나 실패하는지는 측정하는 함수 (오차확인)
손실함수의 경사를 따라 내려오면서 학습 모델(수식)을 업데이트 하는 방법
5-1 결정트리
결정트리 : 머신 러닝의 또 다른 큰 축
캔 와인 판매, 포도주를 캔에 담았다 (내부가 보이지 않음).
3가지 특성으로 포도주의 도수, 당도, Ph 정보를 이용하여 와인의 종류를 구별 (Red/White) 하자.
분류 문제이니, 일단 로지스틱 회귀를 사용해 보자.
(화이트 와인 : 양성 클래스 (1))
로지스틱 회귀로 와인 분류하기
데이터 준비하기

-> 중앙값: 데이터를 일렬로 늘어 놓았을 때, 정 중앙에 있는 값 (!= 평균)
-> info() : 각 열의 데이터 타입, 크기, Null 행 (누락값) 등의 정보 제공 함수
-> describe() : 평균, 표준편차, 최소/최대, 분위수
- 분류 문제 : 기준에 따라 구분/기준의 영향력이 같아야 (스케일 o)
- 회귀 문제 : 인자들의 관계성을 파악 (스케일 x)
- 트리 문제 : 스케일 필요 없음 (각 인자들을 고유의 판단값으로 사용)

-> 데이터와 타겟값 준비 (using numpy)
-> 훈련, 검증 세트 분리 (using train_test_split )
-> 스케일 조정 후, (using StandardScaler)
이제 이진 분류를 위한 로지스틱 회귀를 적용
로지스틱 회귀
이진 분류 로지스틱 회귀 적용 -> 하나의 선형식


-> 0.77769... : 분류 문제의 score 함수로 맞춘 비율(%) 출력 -> 과소 적합 상태
-> 3개의 특성 (도수, 당도, Ph) + 절편 // 알파벳 순서
-> 짐작 : 도수와 당도가 높고, Ph가 낮을 수록 양성 클래스(화이트화인) 가능성 높다.
-> but, 순서도 처럼 쉽게 만들고 싶다.
결정 트리
아주 직관적으로 데이터를 나눌 수 있는 질문의 연속적 반복 (스무고개)
잘 나눌 수 있는 질문을 찾는 과정
계속 질문을 추가하여 분류 정확도를 높임
(질문의 범위는 매우 광범위하고 많은 계산력을 요구)

-> DecisionTreeClassifier : 분류 모델 트리
-> 0.99 : 월등히 좋은 결과, 0.85 : 과대 적합
-> DecisionTreeClassifier ()의 매개변수 가운데 max_feature
: 사용할 feature 개수 지정 (기본값 = none : 모두 사용)
- 분류 : (스무고개 후) 특정 리프 노드에 도착한 샘플들의 다수결
- 회귀 : (스무고개 후) 특정 리프 노드에 도착한 샘플들의 평균값
결정 트리 분석
트리를 단순화하여 분석해보기
당도를 첫 질문으로 사용
전체 6497중 훈련 샘플 5197개
(value=[1258, 3939] : 현재 이 루트 노드의 음성(레드), 양성(화이트) 클래스 개수)
첫 질문인 당도 기준으로 2922 vs. 2275로 자식으로 전달
최종 리프 노드에서 가장 많은 클래스가 예측 결과로 결정 됨
주어진 트리에서는 둘 다 양성이 더 많음

-> max_depth: 깊이 제약
-> filled : 클래스별 색 구분
-> feature_names : 특성 이름 전달

-> 스케일 조정의 결과로 당도가 음수
-> samples : 와인의 개수
-> value = [81, 2194] 같이 뒤에가 더 많은 클래스면 더 진한 파란색
-> 당도 구분이 첫 질문이 된 이유?
당도 구분값으로 -0.239가 선택된 이유?
-> 어느정도의 랜덤성 + 최상의 결과과 제공 트리(from 많은 후보 트리)의 결과물
-> gini 개수를 보고 랜덤하게 결정
결정트리에서의 불순도와 엔트로피
불순도(Impurity)
: 불순도란 다양한 범주(Factor)들의 개체들이 얼마나 포함되어 있는가를 의미
쉽게 말하면 여러 가지의 클래스가 섞여 있는 정도다.
결정트리는 질문해가면서 밑으로 갈 수록 불순도가 낮은 깨끗한 트리여야한다.
지니 지수 : 불순도가 결정되는 정도

엔트로피(Entropy)
: 엔트로피란 데이터의 분포의 순수도(purity)를 나타내는 척도
데이터의 순도가 높을 수록 엔트로피의 값은 낮아지고, 많이 섞이면 섞일수록 엔트로피의 값이 커지게 된다.
정보이득(Information Gain)
: 불순도의 차이
-> 상위 노드는 불순물이 높은 상태로 하위 노드는 깨끗한 상태임 이 차이를 정보 이득
정보이득이 크면 클 수록 하위 노드가 더 잘 구분되었다 -> 정보이득이 큰 방향으로 질문을 해서 들어가자
정보이득이란 어떤 속성을 선택함으로 인해 데이터를 더 잘 구분하게 되는 것을 말하며,
상위노드의 엔트로피에서 하위노드의 엔트로피의 값을 뺀 값이다. (불순도의 차이)
지니 불순도
(1) 각 노드별 지니 불순도 계산
(2) 부모와 자식 노드 사이의 불순도 차이(정보이득)가 가능한 크도록 트리를 성장 시킴

정확히 반씩 나뉠 경우, 최대 불순도 Worst Case (gine=0.5)
한쪽으로만 구분 : 마지막 노드가 순수 노드 (gine=0)
-> 마지막 노드가 순수 노드가 될 때까지 분할 반복 어떻게 분할 할래? 정보이득이 크도록

-> 이런식으로 노드별 지니값와 정보이득값을 계산하여
부모와 자식의 불순도의 차이(정보 이득)가 큰 방향으로 질문 구성하여 트리를 성장시켜 나감
불순도 차이가 크다? 정보 이득이 크다.
부모 노드는 지저분 vs 자식 노드는 깨끗 (o)
-> 이런 질문을 좋은 질문이라 판단하고 질문 이어감
질문에 따라 나뉘는 샘플 수가 달라지고
나뉘어진 그 샘플 내의 음성, 양성 클래스 비율에 따라 자식 노드의 지니 계수가 달라지고
그 뒤 부모 자식 사이의 정보 이득 계산하고,
처음으로 가서 계속 반복 후 정보이득이 가장 큰 최종 질문 선택
(다양한 질문 모두 시도 vs 랜덤 몇 개만 시도) -> 계산 요구량
(참고) 엔트로피 불순도
criterion = 'entropy'로 지정
클래스의 비율을 사용하지만 지니 불순도에서 처럼 제곱을 하는 대신 log2를 취함
일반적으로 지니 불순도와 성능 큰 차이 x
엔트로피 불순도
= – 음성클래스 비율 * log2 (음성클래스비율) – 양성클래스비율 * log2 (양성클래스비율)
= – (1258/5197) * log2 (1258/5197) – (3939/5197) * log2 (3939/5197) = 0.798
-> 이 이후, 정보 이득이 최대가 되도록 질문 내용 조정
가지치기
원래는 결정트리에서 리프노드가 순수 노드가 될 때까지 반복
하지만, 리프노드가 순수 노드가 되면?
너무 많은 학습 요구 시간, 과대 적합의 가능성 O
-> 가지 치기로 극복 (max_depth 값 설정, here 3)
트리에서는 규제를 가지치기로 한다 !
트리 학습은 L2규제/L1규제 적용 불가 (가지치기가 일종의 규제)
선형 방정식의 가중치/절편등을 학습하는 알고리즘이 아님

-> max_depth : 최적의 깊이 설정 (하이퍼파라미터 설정)
-> 깊이1 : 당도 사용, 깊이2 : 당도/도수/PH사용
-> 왼쪽에서 세번째 노드만 음성 클래스가 더 많음
이 노드에 도착해야 레드 와인으로 예측
양성 클래스 : blue (white wile)
음성 클래스 : red (red wile)
스케일 조정하지 않은 특성 사용하기
결정 트리는 선형 함수 학습이 아님 -> 데이터 세트 분할 기준을 학습하는 것
따라서, 스케일 조정 필요 없음
즉, 전처리 필요 없음 -> 특성의 스케일이 학습에 영향을 미치지 않음

-> feature_importances_ : 속성 중요도 (도수는 12% 중요, 강도는 86도 중요 처럼 중요도 평가)
-> 결정 트리의 특성 중요도 출력 속성 (총합 = 1)
어떤 특성이 분류에 가장 유용한지를 나타냄, 당도의 영향력이 가장 큼
-> 스케일 조정이 없어 특성에 음수도 없음
즉, 당도도 양수로 표시되어 이해하기 보다 더 용이
트리의 장점 : 트리를 해석하면서, 분류 체계를 이해하기 쉬움
(참고) 또 다른 가지치기
min_impurity_decrease를 사용하여 가지치기도 가능
-> 부모 노드와 자식 노드와의 (지니) 불순도 차이값
-> 이 경우 보통 비대칭 트리를 생성

-> min_impurity_decrease = 0.0005 : 불순도 감소의 최소치를 정해둠
-> 0.0005 이하면 하지마라는 뜻
(복습)
성분으로 와인 구분 작업 로지스틱 회귀를 이용한 이진 분류 : 가중치, 계수
규제 필요, 특성 정규화, 스케일 조정, 음수값 존재
특성 공학으로 신규 특성 생성
-> 전체적으로 비직관적임
결정 트리 : 가중치 없음 (가중치 규제 방법도 없음, 표준화 과정도 없음),
절편도 없음 단지, 질문을 학습 해 나가는 방법 임
5-2 교차 검증 그리드서치
검증 세트
가능한 테스트 세트는 사용 자제 (마지막 1회 사용)
테스트는 가급적 많이 해 보고 싶은데, 테스트를 더 하는 방법?
훈련이 잘 되고 있는지 훈련 과정에서 계속 확인하고 싶다.

훈련세트를 훈련세트 + 검증세트로 추가 구분
-> 검증 세트를 훈련 세트, 검증 세트, 테스트 세트로
훈련 세트 : 훈련
검증 세트 : 평가
-> 이 과정 반복 테스트 세트로: 최종 평가 단 한번 사용
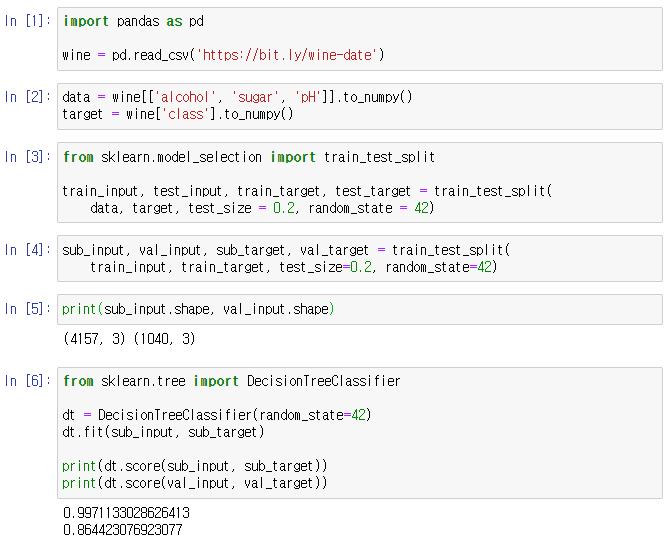
-> train_test_split() 함수를 2회 적용
-> train_input을 추가로 sub_intput + val_input으로 구분
교차 검증
하지만, 검증세트 확보(검증 세트, 테스트 세트 떼내니까)로 훈련세트가 줄어듦 -> 어떻게 극복?
“교차 검증”을 통해 훈련 세트를 더 많이 확보하는 효과를 확보할 수 있다.
cross_validate() : 검증 세트 자동 분할 및 생성 함수
-> train_test_split() 2회 사용할 필요 없음
( 또다른 방법 (모두의 딥러닝) a=StratifiedKfold( ) -> a.split( ) )
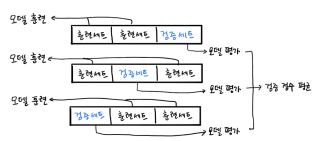
-> 훈련 세트 두 개로 훈련하고 검증세트로 검증
사이킷런의 교차 검증 함수 : 직접 검증 세트 떼어낼 필요 없이 훈련 세트 전체를 넘김

-> dt : 평가할 모델 객체가 첫번째 인자
-> 5겹 교차 검증의 평균 점수가 출력된 모습
-> K-fold 교차 검증 기본 K 값 : 5 (위의 경우 K=3)
-> 훈련 시간, 검증시간, 검증 점수 (주의 : 이름은 테스트지만 각 폴드의 검증 점수임)
: 기본은 5겹 교차 검증 임 (관련 옵션 cv=5) -> 학습을 5번 한 것
-> test_score : 검증 점수
분할기를 사용한 교차 검증
한가지 주의 사항 : cross_validate() 함수는 분할 전 훈련세트를 섞지 않음 (데이터 편향 정렬 주의)
섞기 위해서는 사이킷런의 분할기(splitter)를 사용하여, cv 옵션값으로 지정해야 함
분류 모델의 분할기 : StratifiedKFold (클래스 개수가 잘 섞이도록, 기본 5폴드)
-> 아래 코드 참고) 회귀 모델의 분할기 : KFold

stratifiy in train_test_split() : 이 함수는 기본적으로 훈련세트를 섞어서 나눈다.
특정 feature의 비율까지 고려하여 섞고 싶을 때 사용
혹은 슬라이드의 , 분할기의 좀 더 자세한 설정을 원할 경우, 별도의 객체를 사용
가령, 훈련 세트에 대해 10폴드 (n_splits)로 구분하고, 잘 섞은 후(shuffle) 교차 검증을 수행하고 싶다면
별도의 객체 splitter를 만들어 매개변수 cv에 직접 지정 (10폴드, 섞어라 등)

-> 딥러닝은 교차 검증 잘하지 x
(훈련 + 검증) 1회 + 테스트 1회 (이미 데이터 충분해서)
머신 러닝 쪽은 교차 검증을 주로 사용
그리드 서치
지금까지 검증 세트 자동 분할 및 생성 함수(cross_validate()) 활용 하였음
: train_test_split()을 2회 사용 필요 없는 장점
하지만, 매개변수가 바뀌면 매번 cross_validate() 함수(기본 5겹 교차검증) 호출하여 다시 학습해야 함
E.g.,최적의 max_depth를 찾았다. 이를 고정하고 min_sample_split을 바꾸어 최적의 값을 찾는다?
이로 인해 max_depth도 바뀔 수 있음
즉, 가장 높은 결과를 도출하는 매개변수 및 이들의 조합을 처음부터 다시 찾아야 함
그리드 서치, GridSearchCV()
최적의 하이퍼파라미터 탐색 작업과 교차검증을 동시에 수행하도록 자동화 된 함수
(cross_validate() 함수 호출 필요 없음)
GridSearchCV : 그리드 서치 클래스 (5겹 교차검증 + 매개변수 탐색 자동화)
min_impurity_decrease : 최소 불순도 감소 정도 측정 매개변수 (정보 이득 최솟값 지정 역할)
딕셔너리 = { key1 : value1, key2 : value2…}
value에 문자 숫자 “리스트” 등 사용 가능

-> 기본 5겹 교차 검증 + 5개의 불순도 감소 파라미터 -> 25개의 모델 생성
25개 모델 자동 훈련 후, 가장 높은 매개 변수 조합 생성 결과 dt에 넣음 (즉, 최적 모델 : best_estimator_)
-> value자리에 탐색 매개변수값 리스트를 넣어 파이썬 딕셔너리로 만듦
n_jobs = -1 : 나한테 주어진 가용된 코어의 개수 (-1 모든 코어 사용)
gs.best_estimator_ : 가장 높은 매개변수의 조합 세트

-> 5개 param 각각에 대해, 5겹 교차 검증 수행 평균 결과 (제일 앞 0.0001일 가장 우수)

-> argmax( ) 함수를 이용하여 가장 큰 인덱스값 추출할 수도 있음
-> 0.0001이 베스트 파라미터
만약 매개변수(params)를 더 다양하게 설정?
9*15*10=1350개의 매개변수 조합 * 5겹 교차 검증 = 6750개 모델
-> 그리드 서치로 지정한 조합을 자동으로 찾아준다.
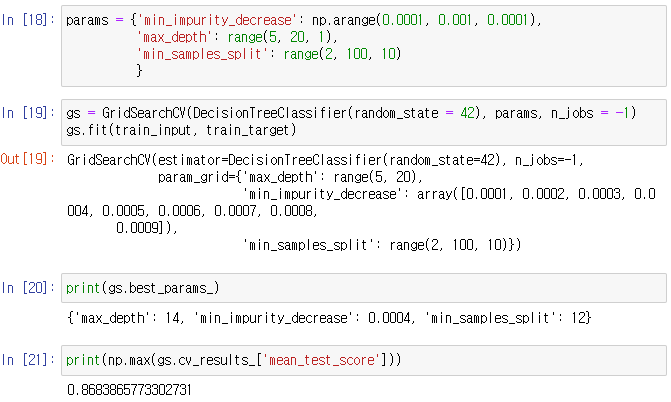
-> min_samples_split : 분할을 위한 최소 샘플 개수
확률 분포 선택
우리는 매개변수를 일일이 바꿔가며 교차검증을 수행하는 대신
매개변수 나열 후 자동으로 검증 수행하여 최상의 매개변수 조합을 찾음 -> 그리드 서치
여기서 매개변수의 후보값을 정할 때, 간격이나 범위를 미리 정하기 힘들 경우
-> 랜덤 서치 활용 : 매개 변수 샘플링을 위한 확률 분포 객체를 전달

-> scipy.status : 싸이파이의 status 서브패키지
-> uniform(실수) randint(랜덤한 정수) 균등 분포 샘플링
-> rvs() : 표본값 무작위 생성 함수

-> unique, return_counts=True : 유니크한 것들을 카운트해서 개수를 보고 싶을 때

-> uniform(0, 1) : 실수일 경우 사용, 난수 발생기와 유사한 효과
랜덤 서치
RandomizedSearchCV : params 범위 내에서 랜덤 샘플링 횟수 지정 (n_iter) 및 이를 위한 클래스

-> gs.best_params_ 출력 : 최적의 매개변수 조합
-> 0.86954282.. : 최적의 매개변수 조합의 교차검증 점수
-> best_estimator : 최적의 모델을 dt로 받아 테스트 세트 수행시 0.86
(참고) 트리의 무작위 분할
splitter = 'random' : 아무렇게나 분류해라
random의 경우 무작위로 분할한 다음 가장 좋은 것을 고름
-> 엑스트라 트리의 기본 분팔 기법

(정리)
검증 세트 validation set
모델을 평가할 때 테스트 세트를 사용하기 않기 위해
훈련 세트에서 다시 떼어 낸 데이터 세트
하이퍼파라미터 튜닝 등의 작업에 효과적
교차 검증 cross validation
훈련 세트를 여러 폴드로 나눈 다음 한 폴드가 검증 세트의 역할
나머지 폴드에서는 모델을 훈련
모든 폴드에 대해 검증 점수를 얻어 평균을 구하는 방법
그리드 서치 Grid Search
하이퍼파라미터 탐색과 교차검증을 자동화해 주는 도구
탐색할 매개변수를 나열해 놓으면
교차 검증을 수행하여 가장 좋은 검증 점수의 매개변수 조합을 선택
마지막으로 선택된 매개변수 조합으로 최종 모델을 훈련
랜덤 서치 Random Search
연속된 매개변수 값을 탐색할 때 유용
탐색할 값을 직접 나열하는 것이 아니라,
탐색 값을 샘플링할 수 있는 확률 분포 객체를 전할
지정된 횟수만큼 샘플링하여 교차 검증을 수행하기 때문에
시스템 자원이 허락하는 만큼 탐색량을 조절할 수 있음
검증세트, 교차검증, 그리드 서치, 랜덤 서치
기존 : 훈련세트 + 테스트세트로 성능 평가 및 하이퍼파라메터 튜닝
테스트 세트는 최종 실전 평가 도구 (일반화 평가 도구)
테스트세트 없이 모델 튜닝을 검증 세트로 하자.
훈련세트+검증세트 -> 최종 모델 도출 후 -> 테스트 세트 최후 적용
검증세트 도입으로 훈련세트 감소 및 이에 대한 극복 : 교차 검증
5-3 앙상블
정형 데이터와 비정형 데이터
- 정형 데이터 : 머신 러닝에 적용, CSV화 할 수 있는 파일
- 비정형 데이터 : 머신 러닝에서는 힘들고, 딥러닝에서 사용 가능 (일반 문장, 사진, 음악 등)
정형 데이터에 가장 우수한 성과를 내는 알고리즘 : 결정트리 기반의 “앙상블 학습”
비정형 데이터는 규칙성을 찾기 어려워 주로 신경망 알고리즘을 이용 (CNN, RNN등)
사이킷런에서 제공하는 앙상블 학습 알고리즘을 알아보기
랜덤 포레스트
앙상블 : 여러 개의 모델을 결합하여 하나의 결과 도출
이러한 앙상블 모델 가운데 하나 : 랜덤 포레스트

결정 트리를 랜덤하게 여러 개 만들어 숲을 형성
트리의 성능을 낮춰 여러개를 보기
랜덤 : 트리의 성능을 낮추는 역할
그냥 두면 트리는 지나친 과대 적합 상태로 진행됨
RandomForestClassifier
RandomForestRegressor
랜덤 포레스트 훈련 방법
랜덤 포레스트의 샘플링 기법 : 부트스트랩 샘플
- 전체 N개의 샘플에 대해 N번 뽑아 옴
- 중복 허용 추출 : 뽑고 집어넣고 샘플을 원래대로 넣기 (중복으로 인한 성능 감소, 트리 다양화)
- 훈련세트와 테스트 세트 크기가 같도록 각각 N개씩 추출
- 결정 트리는 100개 생성
-> 부트스트랩 샘플 : 중복을 허용해서 N번 뽑아 온다.
분류
: 각 100개 결정 트리의 최종 리프 클래스별 확률의 전체 평균을 구하여
가장 높은 확률의 클래스로 예측
hard voting vs. soft voting
회귀
: 각 결정 트리의 최종 타겟 단말 노드 100개의 예측 확률의 평균

중복허용 추출의 문제
훈련 (원원원네) 테스트(세별별별) : 과대 적합 억제 효과
특성의 선택 방법
기존 트리는 쪼갤 때 무슨 최적의 질문할까를 고민
랜덤 포레스트는 만약 3개의 특성이 있으면 루트3 만큼 랜덤 선택
-> 트리의 노드를 분할할 때에도 전체 특성 중 일부 특성을 무작위로 선택하여 진행
(루트를 사용해서 버리고 그 이유가 트리를 덜 똑똑하게 만들려고)

분류 모델 : 전체 특성 개수의 제곱근만큼 랜덤 선택 (과대 적합 방지)
가령, 전체 특성이 4개라면 2개의 특성만 선택
그 뒤, 선택된 2개의 특성으로 최선의 결정 트리를 생성
(윗 그림의 경우 첫 노드는 알코올 도수를 전혀 고려하지 않음)
(회귀 모델 : 전체 특성 사용)
랜덤 포레스트 훈련

-> 교차 검증 수행하기
100개의 결정 트리에 대해 입력데이터의 5겹 교차 검증 수행
: 100개 트리 * 5회

-> cross_validate : 교차 검증 수행
-> RandomForestClassifier : 앙상블 분류 클래스
-> cross_validate에 대해 5겹 교차 검증 수행
-> return_train_score = True : 기본값은 검증 세트 점수만 반환하는데 훈련세트 점수도 보여줌
(과대 적합 파악에 용이)
-> fit() : 특성 중요도 계산을 위해 수행
-> 각 특성 중요도 출력
결정트리보다 좀 더 완만한 결과 (과대적합을 줄이고 일반화된 성능화) 당도 의존성이 낮아짐
oob_score (out fo bag)
샘플을 만드는 또 다른 방법론

oob_score : 부트스트랩에 포함되지 않고 남은 샘플을 사용하여 트리를 다시 평가
1번 트리에 누락 샘플 + 2번 트리의 누락 샘플 + …
끝까지 안뽑히고 남은 애들 모아서 데이터 집합 만들어 검증 샘플 역할 수행
RandomForestClassifier의 자체적 모델 평가 기능을 제공하는 역할
-> 검증 세트로서의 역할도 수행
엑스트라 트리
: splitter = 'random' 으로 만들어진 트리
샘플링 시, 부트스트랩핑 대신 각 트리는 전체 데이터 모두를 사용
즉, 동일한 n 개의 샘플 모두를 훈련/테스트 세트에 사용
노드 분할 시, 성능 억제를 위해 최적 분할 대신 무작위 분할 사용 (splitter = 'random')
분할을 위한 불순도 개념 없음
무작위 랜덤 분할 : 빠른 학습 속도제공
DecisionTreeClassifier(splitter = 'random', random_state = 42) -> 엑스트라 트리가 사용하는 결정 트리
1) 무작위 랜덤분할로 성능은 낮아지지만, 과대 적합 방지 -> 검증 세트 점수 높이는 효과
2) 무작위성이 커 기본 100개 이상의 트리(권장)를 사용하여야 함
3) 무작위 분할로 인해 학습 속도가 빠름
엑스트라 트리를 사용하는 교차 검증

-> ExtraTreeClassifier 클래스 사용
-> 특성 중요도가 결정 트리보다 당도에 대한 의존도가 낮으며, 랜덤 포레스트와 비슷한 결과
(랜덤 포레스트와 엑스트라 트리 비슷)
앙상블의 일반적 알고리즘
: 머신러닝에 있어 여러가지 요소를 모아 최종 결정을 하겠다.
부스팅(boosting) 알고리즘
이전 분류기와 다음 분류기의 결과를 서로 연결하는 방식
여러 개의 약한 학습기를 연결하여 강한 학습기를 만드는 방법
-> 훈련을 반복하여 각 개별 학습기(약결합기)에 가중치 부여(틀린거에 가중치 합산)하고 그 결과를 합산
(그레이디언트 부스트 , 에이다 부스트 (adaptive boosting) 등)

보팅(voting) 알고리즘
여러가지 다른 알고리즘을 같은 데이터에 적용하여 학습
다양한 알고리즘을 분류기로 활용하기때문에, 단일 알고리즘의 단점 극복 가능
여러가지 분류기를 모두 사용해 본 후, 그 중 가장 좋은 분류기를 선택
즉, 다수의 분류기가 선택한 결과를 최종 선택하거나, 클래스별 평균을 종합하여 예측함
배깅(bagging) 알고리즘
데이터 세트를 여러 개로 분리하여 각각 따로 사용 -> 서로 다른 데이터에 대해서 같은 알고리즘 사용
같은 알고리즘의 동일한 다수의 분류기를 각 데이터에 따로 훈련하여
다수의 결과를 통해 최종 결과를 결정
- 배깅은 보팅과 비교하여 하나의 알고리즘을 사용 (대신 데이터가 다름: 부트스트랩 사용)
- 배깅은 부스팅과 비교하여 각 분류기가 제각각 따로 분류 (즉, 별도의 연결(i.e., 합산) 작업을 하지 않음)
보팅과 배깅
(같은 / 다른) 데이터 셋 vs (다른 / 같은) 알고리즘
hard voting vs. soft voting
- 하드 보팅 : 대표값으로 투표하는 방식
- 소프트 보팅 : 각 예측 수치들의 평균을 다시 구하는 방식
ex) 미국 대통령 선거 결과
국민들의 투표 vs 선거인단의 대표 투표
그레이디언트 부스팅
그레이디언트? 손실함수의 최저점을 찾는 방법 (오차 줄이기 기법)
- 분류 손실함수 : 로직스틱손실함수(log)
- 회귀 손실함수 : 평균 제곱오차(MSE)
그레이디언트 부스팅
: 앙상블 알고리즘 가운데 일반적으로 가장 성능이 좋은 알고리즘
(트리에 경사하강 같은걸 만들어 넣자.)
손실이 낮아지도록 (i.e., 오차 줄이기) 결정 트리를 계속 추가하는 방법
결정 트리의 결과값으로 분류/회귀 결과 예측 (like 활성화 함수 결과값)
이때 트리의 최종 예측값을 오차 함수에 대입하여 오차 확인
분류 : 로지스틱 손실 함수 (log)
회귀 : 평균제곱오차 함수 (MSE)
이 오차가 줄어드는 방향으로 질문을 재구성한 신규 트리 생성 및 앙상블에 트리 추가
즉, 현 트리의 결과값을 분석하여 오차가 낮아 지는 방향으로 새로운 트리를 순차적으로 추가
(깊이가 3인 첫번째 얕은 트리의 오차를 추가한 후
두번째 트리를 넣어가며 트리를 하나씩 순차적으로 추가하며
오차가 줄어드는 트리 찾기)
-> 깊이가 얕은 결정 트리를 계속 순차적으로 추가하여 손실(오차) 보완
(기본값 : 깊이가 3인 얕은 트리 100개 사용)
학습률 매개변수로 학습 속도 조정 가능
깊이가 얕아 과대 적합에 매우 강하고, 일반적으로 높은 성능 제공
트리를 순서대로 추가함으로 병렬성 결여 -> 학습 속도가 느리고, n_job 매개 변수가 없음
그레디언트 부스팅과 교차 검증의 적용

-> 과대 적합이 거의 발생하지 않음
트리 개수 500개로 조정

-> n_estimators : 500번 트리를 넣겠다.
-> learning_rate = 0.2 : 학습률로 이동 속도 조정 매개 변수 조정 후 다시 한번 해 보자.
-> 트리 개수가 500개이지만, 과대 적합이 잘 억제되고 있음 (94% 정도는 ok w.r.t. 99%)

-> 특성 중요도 확인 가능
히스토그램 기반 그레이디언트 부스팅
히스토그램 : 훈련데이터 샘플을 256개의 구간으로 구분 (즉, 전체 데이터를 256개의 그룹으로 나눔)
전체 데이터가 아닌 1/256개의 데이터로 깊이 3인 트리를 계속 추가하기 때문에 트리 최적화 속도가 더 빠름
(즉, 오차를 줄이기 위한 최적 분할용 질문 선택을 보다 더 빠르게 수행)
256개의 구간은 = 255 + 1 (누락 값을 가진 샘플들은 모아서 이 구간에 자동 추가시킴)
따라서, 샘플값 누락에 따른 전처리 과정등에 신경 쓸 필요 없음

-> experimental : 현재 실험적 패키지
HistGradientBoostingClassifier
-> 과대적합을 잘 억제하면서
앞 슬라이드의 기본 그레이디언트 부스팅보다 조금 더 좋은 성능
(c.f., 500회 수행보다는 약간 낮음)
Permutation Importance (특성 중요도)
히스토그램기반 GB에서도 특성 중요도를 계산해 보자.
히스토그램기반 GB는 기존 앙상블에 존재한 특성 중요도 (feature_importances_) 속성이 없음
이를 위해 permutation_importnace() 함수를 사용
첫번째, 두번째, 세번째 특성을 각각 무작위로 섞고
성능 가장 떨어진 것 -> 제일 중요한 특성

-> rf 객체를 이용한 feature_importances를 구하고 있음
rf : random forest 객체
-> 분류기이기 때문에 합이 1이 아니고, 정확도의 차이로 계산,
두번째 특성(당도)을 섞으니 정확도가 23% 정도 감소함을 의미
Permutation의 의미?
샘플의 각 열을 기준으로
각 열의 특성 다 섞고, 나머지는 그대로 사용, 전체 성능 감소 여부 계산하여
성능 감소가 가장 큰 특성이 중요한 특성
XGBoost vs LightGBM
사이킷런 이외의 히스토그램 기반 GB 알고리즘 지원 라이브러리 : XGBoost, LightGBM
코랩에서 사용가능하며, cross_validate() 함수와도 같이 사용 가능

XGBClassifier(tree_method = 'hist') : 이 옵션을 통해 히스토그램 기반 GB 사용 가능
LGBMClassifier : 마이크로 소프트사의 히스토그램 기반 GB 라이브러리
(정리)
앙상블 학습 Ensemble Learning
더 좋은 예측 결과를 만들기 위해 여러 개의 모델을 훈련하는 머신러닝 알고리즘
정형 데이터를 다루는 데 가장 뛰어난 성과를 내는 알고리즘
대부분 결정 트리를 기반으로 만들어져 있음
랜덤 포레스트 Random Forest
대표적인 결정 트리 기반의 앙상블 학습 방법
부트스트랩 샘플을 사용
랜덤하게 일부 특성을 선택하여 트리를 만드는 것이 특징
랜덤하게 선택한 샘플과 특성을 사용하기 때문에 훈련세트에 과대적합되는 것을 막아준다
검증세트와 테스트세트에서 안정적인 성능을 얻을 수 있다
부트스트랩 샘플(bootstrap sample)
무작위로 중복을 허용해서 선택한 n개의 데이터를 선택하는 과정을 거쳐 도출되는 샘플
OOB(out of bag) 샘플
부트스트랩 샘플에 포함되지 않은 샘플
엑스트라 트리 Extra Trees
랜덤 포레스트와 비슷하게 결정 트리를 사용하여 앙상블 모델을 만들지만,
부트스트랩 샘플을 사용하지 않고 전체 데이터 사용
대신 랜덤하게 노드를 분할해 과대적합을 감소
랜덤 분할로 인한 무작위성이 커서 학습 속도가 빠름
무작위성이 커 100개 이상의 트리를 사용하길 권장
그레이디언트 부스팅 Gradient Boosting
랜덤 포레스트나 엑스트라 트리와 달리 결정 트리를 순차적으로 추가하여
손실 함수를 최소화하는 부스팅 기반 앙상블 방법
깊이가 얕은 (depth 3) 트리를 계속 추가하여 오차를 보완해 나감
깊이가 얖은 트리를 사용하기 때문에 과대 적합에 강함
학습 속도가 조금 느리지만 (트리의 순차 추가), 일반적으로 좋은 성능을 기대할 수 있음
히스토그램 기반 그레이디언트 부스팅 Histogram-based Gradient Boosting
그래이디언트 부스팅의 속도를 개선한 것
입력 데이터(훈련 데이터)를 256개의 구간(작은 데이터 사용, 빠른 학습)으로 나누며,
노드를 분할할 때 최적의 분할(오차를 감소시키는 방향으로의)을 빠르게 찾을 수 있음
사진 출처 : 혼자 공부하는 머신러닝 + 딥러닝 강의자료
'파이썬 & 머신러닝과 딥러닝' 카테고리의 다른 글
| 16일차 - 딥러닝의 역사, 퍼셉트론, 다층 퍼셉트론, 역전파 알고리즘 상세, 활성화 함수 및 원리 (0) | 2024.02.01 |
|---|---|
| 15일차 - 비지도 학습, 군집 알고리즘, k-평균, 차원축소, 주성분 분석 (2) | 2024.01.31 |
| 13일차 - 로지스틱 회귀, 딥러닝을 위한 기초수학, 선형 회귀, 경사하강, 다중 선형 회귀 (2) | 2024.01.29 |
| 12일차 - k-최근접 이웃 회귀, 선형회귀, 다항 회귀, 다중 분류, 특성공학, 규제 선형 모델 (0) | 2024.01.26 |
| 11일차 - 머신러닝과 딥러닝의 기본 원리, 훈련세트와 테스트세트, 데이터 전처리 (1) | 2024.01.25 |



