(복습)
결정트리
높은 성능, 과대 적합이 되기 굉장히 쉬움
결정 트리를 활용한 앙상블 알고리즘
원본데이터 대신 중복된 샘플 데이터 사용
무작위성 주입 -> 의도적 성능 감소
랜덤 선택 주입 -> 의도적 성능 감소
6-1 비지도 군집
비지도 학습
비지도 학습 : 군집, 차원 축소
과일 사진을 종류별로 모아 보자.
사용자가 처음부터 무슨 과일을 올릴지 모름
(타겟이 없음, 특성 데이터만 존재)
과일을 종류대로 분류해서 모으기
-> 사진을 보고 과일 사진을 자동으로 분류하자
기본 아이디어 : 과일 사진의 픽셀 값을 모두 평균 내면 비슷한 과일끼리 모일까?
과일 사진 데이터 준비하기
일단, 과일 데이터를 다음 3가지로 고정하자
: 사과, 바나나, 파인애플 (기본 가정, 문제 풀이의 제약조건)

-> 파이썬 코드가 아닌 쉘 명령어로 실행
-> wget : 원격 주소에서 데이터 다운로드 후 저장
-> -O : 파일 이름 저장

-> 사진 하나하나가 100 by 100 픽셀
-> fruits_300.npy : 300개의 샘플 (100 by 100)
-> 넘파이 load() : 넘파이 배열 형태로 반환
샘플 확인
첫번째 샘플의 첫번째 행의 모든 열(100)만 출력하여 확인해 보자
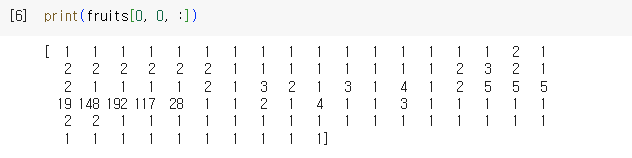


-> imshow : 넘파이배열 값을 이미지로 출력하는 함수
-> cmap=‘gray’ : 흑백으로 출력 ( 이 그림의 첫줄 : 사과 꼭지 흰부분 참고 0 : 검은색, 255 : 흰색 )
바탕이 검은색 (픽셀값 0) 사람이 보기엔 불편
-> cmap=‘gray_r’ : 반전 이미지 ( 밝은 부분 0, 어두운 부분 255 ) 로 보는게 편하다.

-> 100번째, 200번째는 각각 파인애플, 바나나가 출력됨
0~99 : 사과 / 100~199: 파인애플 / 200~299: 바나나
즉, 각 3가지 과일이 100장씩 있는 상태
-> axs : 일반 변수
-> 캔버스 같은 두 사진 전체가 fig, 처음 사진이 axs[0], 두번째 사진이 axs[1]
픽셀 값 분석하기
샘플 차원 변경하기
우리가 사용하는 데이터는 100개씩 과일 종류가 나누어져 있음
0~99 사과 / 100~199 파인애플 /200~299 바나나
2차원 이미지를 1차원 이미지로 변환
Why? 이미지로의 출력은 어렵지만 배열값 계산할 때 용이함

-> Reshape from (300, 100, 100) to (300, 10000)
-> reshape (-1, …) : -1의 의미는 행에 -1을 썼을 경우,
행(-1)의 개수가 열에 정해진 숫자에 따라 모든 원소가
빠짐없이 배치될 수 있도록 가변적으로 정해짐을 의미 (행의 개수가 가변)
( 첫번째 차원을 -1로 지정하면
데이터들은 남은 차원(여기서는 column)에 자동으로 할당
첫번째 차원(row)은 샘플의 개수를 의미)
->1차원 배열로 구성된 10000개의 픽셀로 구성된 100개의 사과 출력됨

샘플 평균의 히스토그램
과일의 구분을 위해 각 과일 샘플(만개 픽셀)의 평균값을 계산 해 보자.

-> 맷플로립의 hist() : 히스토그램을 그려주는 함수
-> axis = 1 : 열을 바꿔가면서 이동하며 특정 행의 통계값 계산
-> alpha : 투명도 지정
-> legend : 범례
-> X축 : 구간(샘플들의 평균값) , Y축: 빈도 -> 히스토그램 그래프
가령, X축에서 평균이 20~35정도인 바나나가 22정도 있더라…
-> 히스토그램을 통해 분포 확인 가능
-> 사과와 파인애플 구분 모호한 결과
과일의 구분을 위해 각 과일 샘플(만개 픽셀)의 평균값을 계산

-> 100개 사과 각각에 대한 픽셀 평균 값 (대략 80~95 사이)
-> 샘플의 평균값으로는 구분 어렵
픽셀 평균의 히스토그램
각 과일의 샘플의 평균 대신, 이번에는 픽셀의 평균값을 계산 해 보자.
(각 샘플의 픽셀 위치별 평균) axis = 0 : 행을 따라 이동하며 계산(평균)
(사과 전체의 평균 보기 -> 각 사과 이미지의 특정 위치의 평균 보기)

-> axis = 0 : 가령 사과의 경우 (100, 10000) 각 column별 평균
-> 각 과일의 같은 위치의 픽셀들 전체 만개에 대한 그림 (중복되는건 빈공간 없이 나옴)
(가운데가 나왓다 바나나, 전체적으로 뚱뚱하다 파인애플 이런식으로 구분 가능)
-> 3가지 과일의 픽셀 위치가 구분됨
X축 : 각 그림의 1000개의 픽셀 / Y축 : 픽셀 평균 값
평균 이미지 그리기
이번에는, 10000개의 픽셀 요소로 이루어진 1차원 배열의 평균값을 100by100으로 그려보자.
-> 이미지를 모두 합쳐 놓은 대표 이미지 (or 평균 이미지)
: 각 픽셀의 평균값을 대표 픽셀로 하여, 이 픽셀 10000개로 그림을 그리자
-> 즉, 각 과일 100개의 평균 이미지를 평균값을 가지는 각 픽셀 1만개로 과일 다시 그리기

-> 모든 샘플의 각 픽셀 위치에 평균값이 찍혀 전체적으로 흐릿한 느낌
평균값과 가까운 사진 고르기
평균과 가까운 사진 고르기: 사과
사과 사진의 평균값 (apple_mean)과 가장 가까운 사진을 골라보자.
-> 모든 샘플에 대해 100by100 형태의 apple_mean을 뺀 절댓값의 평균을 계산
-> 그 값이 작은 순서대로 100개 고르자.


-> 군집(clustering)화 작업 결과 출력됨
-> abs() : 절대값
- fruit (300, 100, 100) // axis0, axis1, axis2 -> 전체 과일 사진
- apple_mean (100,100) -> 사과 평균
- abs_diff (300, 100, 100) -> 과일과 사과 평균의 차이
-> abs_mean : 1차원 (300, )
( 두번째, 세번째 차원의 평균 -> 300개의 일차원 배열로 생성 (300, ))
-> argsort() : abs_mean 배열 정렬 함수 (앞의 100개만 출력 (오차가 작은순으로 정렬) )
axis(1,2) : 2번째, 3번째 축을 움직이면서(즉, 각 한장의 그림) 0번째 축의 통계값 계산
--> 이 경우 각 그림(axis = 0) 절대값의 평균
(참고) 평균과 가까운 사진 고르기: 바나나

흑백 사진의 픽셀값을 이용하여 과일 사진을 모으는 작업을 진행하였음
비슷한 샘플끼리 모으는 작업 : 군집 (클러스터, cluster) -> 대표적 비지도 학습
한계) 우리는 이미 어떤 이미지인지 알고 있었다. 즉 타겟값을 알고 있었다.
실제 비지도 학습에서는 타겟을 모르기 때문에 샘플별 평균을 구할 수 없다. -> 6.2로
6-2 k-평균
샘플의 평균 (과일을 종류별로 분류하는 문제) vs.
픽셀들의 평균 (모든 샘플에 대한 같은 픽셀위치들의 평균)
군집
: 대표적인 비지도 학습
타겟이 뭔지 알려주지 않고 모으기
< 현재 상황을 정리해 보면 >
이전 방식은 이미지들의 클래스 개수와 클래스별 샘플수를 알고 있었음
(처음 100개는 사과, 그 다음은 파인애플…)
-> 그 정보를 바탕으로 클래스별 평균을 구함
-> 실제는 어떤 과일이 있는지 타겟을 모름
이 경우, K-평균 군집 알고리즘 : 평균값을 구하는 알고리즘
-> 클러스터 중심을 찾는 과정 (평균 이미지를 찾는 과정)을 제공하는 알고리즘
중심과 가까운 애들이 클러스터 중심 (차이를 구하는 것이 중요)
클래스 자동 구분 후, 평균값 자동 계산
찾아진 평균값 : 평균 이미지 == 클러스터 중심 (센트로이드)라 함
여전한 한계) 무슨 과일인지는 몰라도 몇 type인지는 알려줌 (K 값)
k-평균
1. 무작위로 K개(given, 하이퍼파라미터)의 클러스터 중심(클러스터 평균)을 선정 (i.e., 무작위 집합별 평균값 구하기)
1-1 각 샘플들은 각 중심과 자신의 중심 사이의 거리를 계산
(중심이란? 픽셀값들의 평균값, 거리란? 픽셀값들의 차이값)
2. 각 샘플들은 가까운 중심을 찾아 해당 클러스터 형성
3. 형성된 클러스터 내의 샘플들의 평균(중심) 다시 계산
3-1 새롭게 계산된 평균값으로 클러스터 중심 변경(갱신)
4. 다시 1-1 로
클러스터의 개체의 변동이 없으면 (혹, n_iter 지정 횟수 후) 중지 -> 클러스터링 되었다.
즉, 클러스터 중심 구하고 중심과 사과간의 거리 측정
오차가 더 작은 쪽으로 이동 후 중심 잡고 다시 거리 측정, 변동 없을 때 까지 반복

다수 과일의 특징 쪽으로 중심이 이동함 (빨간 점은 임의로 잡은 덩어리의 클러스터 중심)
클러스터 중심 = 평균 이미지
중심까지의 거리 = 평균 이미지와의 오차값
세 점 가운데 가장 오차가 작은 이미지 집합으로 이동
-> 재구성된 집합으로 평균 이미지 다시 구하기
-> 각 평균 이미지에 대한 오차 다시 계산 -> 반복
사이킷런의 K-평균 모델 만들기
모델 훈련

-> 데이터를 불러와 3차원 배열 2차원으로 변환 (샘플, 너비 * 높이)
-> KMeans
-> n_clusters = 3 : 클러스터 개수 지정
-> km.fit(fruits_2d) : 비지도 학습 (타겟 데이터 없음)
-> km.labels_ : 군집된 결과가 저장된 속성
-> 이 상황에서 0, 1, 2가 각각 무슨 과일인지를 모름

-> np.unique(.., return_counts = True) : 클래스별 유니크 값 출력 및 그 개수 출력
첫 번째 클러스터
각 클러스터 0/1/2가 무엇인지 이미지를 그려보자.
즉, 출력 함수draw_fruits()를 파이썬으로 제작 해보기



-> ratio : 그림 크기 결정
-> row 하나면 column는 샘플 개수, 아니면 column 10개
-> squeeze = False : 항상 2차원 배열로 생성
-> 불리언 인덱싱을 이용하여 원하는 원소 선택
(레이블이 0인게 참인것만 선택)
-> axis('off') : 좌표축 생략
-> Label0이 사과임을 확인
두 번째, 세 번째 클러스터
완벽하게 구분하지는 못함
하지만, 타겟 레이블을 전혀 제공하지 않았음에도
스스로 비슷한 샘플을 잘 모은 것 같음
(단, 한계는 군집의 개수(k)를 미리 지정한 상황이라는 점)

클러스터 중심
Kmeans 클래스가 최종적으로 찾은 속성은 cluster_centers_ 속성에 저장 됨
각 샘플의 클러스터 중심의 그림을 그려 보자.
클러스터 중심 : 클러스터에 속한 샘플들의 특성 평균값

-> 모든 과일에 대해 10000 픽셀을 다시 (100,100)로 변환
클러스터 중심 저장 속성 : cluster_centers_
모든 과일에 대한 클러스터 중심 속성 출력 (앞서 살펴본 픽셀의 평균값과 사실상 동일)
즉, 평균 이미지 = 클러스터 평균 = 클러스터 중심

-> transform() : 샘플에서 클러스터 중심까지의 거리 변환 함수 (100번째 샘플의 경우 3393.81…이 최소)
-> predict() : 가장 가까운 클러스터 중심을 예측하는 함수
참고) 같은 함수명, 다른 기능
-> km.n_iter_ : 알고리즘이 반복한 횟수 확인
즉, 클러스터 중심이 이동한 횟수
-> 여전한 한계 : 타겟을 사용하지 않았지만, n_clusters 지정 (=3) 해 줌
최적의 k 찾기
K-평균 알고리즘의 단점 ?
k개로 분류하겠다로 클러스터 개수(k)를 사전에 지정해야 함
실전에서는 몇 개의 클러스터가 있는지 알 수 없음
최적의 K를 자동으로 찾는 알고리즘?
엘보우 알고리즘 : 적절한 클러스터 개수 찾아주는 기법
이너셔(inertia_) : 클러스터에 속한 샘플이 얼마나 가깝게 모여 있는지 보여주는 지표
(학습해서 찾은 속성) -> 거리의 제곱들의 합
클러스터 개수 증가 -> 이너셔 감소 이너셔 감소의 변곡점 구간(꺾이는 지점) 확인

-> 군집 개수 변경하여 반복 실행 (2~7개)
-> inertia_ : 거리의 제곱의 합
-> 거리의 제곱의 합(inertia_) 지표를 inertia 리스트에 추가
비지도 학습의 일반적 용도
비지도학습 -> 군집(클러스터링) -> 해당 정보를 바탕으로 후속 지도학습에 적용
군집 알고리즘 : 타겟이 없는 비지도학습
K-평균 알고리즘을 활용한 클러스터 중심 계산
-> 특성에 영향을 받으므로, 스케일 조정 필요
단점) 클러스터 개수 사전 지정
극복) 엘보우 알고리즘
6-3 주성분 분석
차원 축소
비지도 학습의 또 다른 대표 분야 : 차원 축소
이때 말하는 차원 축소 : 특성의 개수 줄이기
전체 샘플 수의 증가 & 샘플 하나하나의 정보 증가
특성 (차원) : 샘플이 가진 각각의 속성
차원 축소 : 특성이 너무 많으면 과대 적합
따라서, 데이터의 특징을 가장 잘 나타내는
일부 특성만 선택하여 데이터의 크기를 줄이고,
지도학습의 성능을 향상 시키자
대표적 차원 축소 알고리즘 : 주성분 분석 (PCA, Principle Component Analysis)

주의) 데이터의 특성을 회손하지 않는 범위 내에서 특성의 개수를 줄이는 차원 축소임
3차원 배열을 2차원으로 줄이는 개념이 아님.
차원 축소 : 특성 수 감소 (e.g., 3개 특성을 2개 특성으로 (n,3) -> (n,2)) : 둘다 2차원 배열 !
차원 축소 개요
차원 축소의 필요성
: 차원이 커질수록 데이터 포인터간의 거리가 늘어남 (데이터 희소화)
거리 기반 학습 성능 저하, 포인터간 상관관계 파악도 난해
차원 축소의 잇점
: 학습 시간 절약 3차원 이하로 축소시켜 시각적 확인 용이 (데이터 패턴 인지)
-> 특성들의 상관 관계에 대한 시각화
차원 축소의 목표
: 어떻게 하면 원본 데이터의 정보를 최대한 유지한 채로 차원 축소를 할 것인가?
- 특성 선택 (Feature Selection) : 특징을 잘 반영하는 주요 피처만 선택
- 특성 추출 (Feature Extraction) : 기존 특성 함축하여 요약하여 새롭게 만들어낸 특성 (재조정)
-> 특성 추출 : 피처의 단순 압축이 아닌, 피처를 함축적으로 더 잘 설명할 수 있는 또 다른 공간으로 매핑
ex) 모의고사 성적, 대외활동, 봉사활동, 수능성적, 수상 경력, 종합내신 성적
-> 학업 성취도, 커뮤니케이션, 문제 해결력
6개의 특성을 상호 섞어져서 3개의 특성으로 함축적 설명
주성분 분석 (PCA)
차원 축소의 대표적 알고리즘 : 주성분 분석 PCA (그 외, LDA, SVD, NMF …)
주성분 분석 (PCA)이란?
데이터에 가장 많이 퍼져 있는 데이터의 방향성을 찾는 과정 (분산이 큰 방향을 찾는 것)
그 방향이 주성분
특성이 2개 (x1, x2) 인 이차원 데이터 주어진 데이터에서 분산이 큰 방향인 벡터를 찾음
-> 분산 데이터를 원점에 맞추어 줌 (계산하기 쉬우라고) -> 주성분 하나를 찾았다는 뜻
주성분 1개 : (2,1) -> 원점 이동 및 벡터의 좌표식 표현
이 벡터를 주성분(PC)라 함
주성분이 기존의 n개의 특성으로 표시됨
주성분 벡터의 원소 개수 = 특성 개수 = 2 (*)
즉, 주성분이 기존 특성들 N개의 조합으로 표현됨
-> 샘플 데이터 (4,2)를 주성분 벡터에 직각 투영 (정사형) : (4,2)가 줄어 1차원 데이터 4.5 획득
2개의 특성(4,2)을 1개의 특성(4.5)으로 줄임 (**)
(주성분 원소의 개수는 줄어들지 x 특성의 개수와 같다.)
-> 첫번째 주성분 분산이 큰 방향으로 찾은 것임
-> 원 주성분의 수직인 방향으로 두번째 주성분 찾음 (원본 특성의수만큼 주성분 존재)
주의) 주성분 원소수는 원본 차원수과 같고 (*),
주성분으로 바꾼 데이터는 차원이 줄어 듦 (**)
PCA 개요
원본 데이터의 변동성이 가장 큰 방향으로 순차적으로 축을 생성
이 축으로 데이터를 투영하는 방식
ex) 키가 커지면서 몸무게가 커지는 변동성(우상향)만 반영

-> 첫번째 PCA 축 (변동성이 큰 방향)으로
두번재 축 생성, 첫번재 축의 직각 방향
PCA 과정
원본 데이터의 공분산 행렬 추출
-> 공분산 행렬을 고유 벡터와 고유값 분해
-> 원본 데이터를 고유 벡터로 선형 변환
-> PCA 변환값 도출
--> 변동성 확인을 위해 공분산 행렬 사용
공분산이란?
두 변수간의 변동성 의미 (상관도)를 행렬로 만든 것
(정방행렬, 대칭행렬 형태)
ex) Cov(X, Y) > 0 : 키가 증가시 몸무게도 증가함을 의미
즉, 양의 상관관계가 있고 그 정도가 0.28(Z, Y) 의미

훈련세트를 공분산 행렬로 변형한 뒤,
다시 아래의 3개 행렬 곱셈으로 분해

공분산 행렬은 대칭행렬이며, 대칭행렬은 다음 특성을 가짐
대칭 행렬은 직교 대각화가 가능 (대칭 행렬은 고유 값으로 표현 가능하다.)
-> 직교행렬 (고유벡터) * 정방행렬(고유값) * 전치행렬(직교행렬의)로 분해 가능
여기서, 고유벡터 [e1, e2, en]들이 생성되고,
e1이 첫번째 고유벡터의 크기
e1은 가장 분산이 큰 방향으로의 고유백터 (즉 PCA 축),
e2는 e1에 수직이면서 다음 분산의 방향....
고유값이 크면 분산의 정도가 가장 크다 (데이터의 경향을 가장 잘 반영한다)
공분산 행렬에서 고유값이 가장 큰 순으로 고유벡터를 추출
이 고유벡터를 이용하여 원본 데이터를 선형 변환(정사영)하는 것 : PCA
고유벡터
2차원에서는 2개, 3차원에서는 3개,... N 차원에서 N개 존재
5개의 행 각각에 고유 벡터 존재,
5개의 특성으로 5차원 벡터임 (5개의 좌표) : 5개의 고유 백터
[e1,.., en] 값에 해당 (주의) 1 by n 행렬이 아님
고유값
고유 벡터의 크기
고유값이 큰 순서대로 정렬됨
고유벡터 행렬의 각 행(각 벡터)들에 대응하는 고유값
(그 외 다양한 차원 축소 기법)
LDA (Linear Discriminant Analysis, 선형 판별법)
SVD (Singular Value Decomposition, 특이값분해법)
INME (Non-Negative Matrix Factorization, 행렬분해법)
주성분 분석(PCA) 클래스
실제 주성분 분석을 통해 특성의 개수를 줄여보기
참고, PCA도 특심이 스케일에 영향을 받으므로 전처리 필요
주어진 예제는 스케일이 모두 동일함으로 생략

-> PCA : 주성분 분석 클래스
-> n_components = 50 : 10000개 중 찾을 주성분의 개수 50개로 지정
-> fit(fruits_2d) : 2차원 변환 데이터, 타겟 데이터 없음
-> (50, 10000) -> 찾은 50개 주성분, 주성분의 원소수는 원본 데이터의 특성 개수 즉 픽셀 10000개와 같음
주성분 50개 이미지를 2d 형태로 그려보기
주성분 확인을 위해 앞서 구현한 draw_fruits() 함수 활용

-> 각각의 주성분이 어떻게 그려진지 그래프로 나타난 형태
점점 밑으로 갈 수록 추상화가 이루어짐 (앞으로 갈수록 데이터의 특징을 잘 잡아냄)
-> 데이터 셋의 어떤 특징을 잡아낸 형태
원본 데이터를 주 성분으로 분해하는 것
원본 데이터에서 분산이 큰 방향의 순서대로 나타낸 것

-> 원본 데이터는 300개 샘플에 대해 각각 만개의 특성을 가졌음

-> 변환 데이터는 300개 샘플에 대해 각각 50개의 특성
: 원래 2d 데이터의 10,000개의 특성을 50개의 특성으로 줄임 (**)
원본 데이터 재구성
50개의 특성을 다시 10000개로 복원
특성을 줄였다 -> 데이터 손실 발생
다시 원본으로 복원할 수 있을까?
10,000개 특성 -> 50개 특성으로 1/200로 감소
다시 원본 복원? 어느 정도 손실은 발생 상당 부분 재구성 가능 : inverse_tranform()




-> inverse_transform() : 원본을 다시 복원하는 PCA 클래스의 메소드
-> 만개로 복원 (!= 저장된 기존 이미지로의 환원)
정확히는 복원이라기 보다는 50개 특성으로 10000개의 픽셀을 만들어 냄
-> 상당 부분 재구성 가능
-> 이 후, 다시 draw_fruits() 함수 호출로 fruits_reconstruct를 각 과일로 그려보면
배경, 주변부 흐릿 대략 과일 구분은 가능
설명된 분산 (Explained Variance)
복원이 어느 정도 수준으로 된 것인지 확인해보자
설명된 분산 (원본 복원 품질률)
: 주성분이 원본 데이터의 분산을 얼마나 잘 나타내었는가를 표시

-> pca.explained_variance_ratio_ : 각 주성분의 설명된 분산 비율의 합이 저장된 속성
-> 50개의 특성으로 92.15%의 복원률을 보임 (92%의 품질)

-> 주성분 개수에 따라 plot 그리기
-> 50개의 단계별 품질 손상률을 보여줌
-> 각 주성분별 분산 비율 표시
50개 주성분의 총합 : 약 0.92 (약, 92%의 품질 유지)
처음 10개의 주성분이 사실상 대부분을 차지
만개 -> 50개 -> 핵심 10개
<다른 알고리즘과 함께 사용하기>
이제, PCA로 차원 축소된 데이터를 사용하여
지도 학습 모델을 훈련해 보자.
그리고 이를 원본 데이터를 사용했을 때와의 차이를 비교 분석 하자.
지도학습 분류기와 함께 사용하기
사례 1) 차원 축소된 데이터의 성능을 확인 해 보자.
(차원 축소 데이터 vs. 원본 데이터) -> 지도학습에 활용
로지스틱 회귀를 사용한 분류에 차원 축소 데이터를 적용해 보기

fruits_2d : 지도 학습은 타겟 필요, 임의의 타겟 0/1/2 지정
-> scores['test_score'] : 원본과 타겟을 이용한 교차 검증 수행
-> socres['fit_time'] : 훈련 시간 확인
-> 차원축소본과 타겟을 이용한 교차 검증 수행시 훈련 시간 감소 (by 차원 감소)
-> 정확도는 0.996 vs 1.0 (오차범위), 훈련시간 대폭 감소
주성분의 개수(정수)를 지정하는 대신
설명된 분산의 비율로 지정 가능 (실수)
실수값을 주면 설명된 분산의 희망 합계를 지칭함 (0.5, 즉 50%)
2개의 특성으로 줄이기

-> PCA component 주성분 2개 만으로 50% 분산 확인 가능
-> (300, 2) : 300개의 샘플이 2개의 특성만 가지게 됨
-> 2개의 특성 -> 99% 정확도
-> 오차 범위내의 시간 증가 (trivial)
오차범위 내에서 시간이 약간 증가되고 99%의 정확도로 문제 되는 것은 x
군집과 함께 사용하기
사례 2) 이번에는 차원 축소된 데이터의 성능을 군집을 통해 확인 해 보자.
차원 축소 데이터를 활용하여 K-평균 알고리즘으로 클러스터를 찾아보자.




-> n_clusters = 3 : 군집수 3개로 지정 (실전에서는 모름)
-> 앞서 학습된 2개의 특성으로 차원 감소된 데이터 활용
-> 원본데이터 91, 98, 111 와 거의 비슷한 결과 출력됨
시각화
차원 축소의 또 다른 장저머 : 차원을 3개 이하로 줄이면 시각화에 용이
-> 3차원보다 큰 차원은 그래프로 그리기 어렵다.
fruit_pca는 현재 2차원까지 줄였음, 이를 그래프로 표시 해 보자.

-> data[:, 0], data[:, 1] : (모든 데이터의 차원 0, 모든 데이터의 차원 1)을 산포
-> 왼쪽 상단 : 차원1, 우측 하단 : 차원 0
-> 데이터의 시각화를 통해 예상치 못한 통찰을 얻을 수 있음
(참고) Iris 데이터의 시각화
붓꽃은 4개의 특성 가짐
그 중 특성 2개로 3가지 붓꽃을 구분해보자 (3진 분류)

PCA 차원 축소를 적용하여 2개의 특성으로 그려보기
-> 좀 더 구분이 잘되는 형태

(정리)
차원 축소
- 데이터 셋의 크기 감소
- 훈련 시간 감소
- 과대 적합 방지
- 시각화 용이
차원 축소된 데이터는 지도 학습 혹은 비지도 학습에 사용 가능
사진 출처 : 혼자 공부하는 머신러닝 + 딥러닝 강의자료
'파이썬 & 머신러닝과 딥러닝' 카테고리의 다른 글
| 17일차 - 크로스엔트로피, 다층 신경망 그래디언트 소멸, 하이퍼파라미터 최적화, 손실 곡선, 검증 손실, 드롭아웃, 모델 저장과 복원 (0) | 2024.02.02 |
|---|---|
| 16일차 - 딥러닝의 역사, 퍼셉트론, 다층 퍼셉트론, 역전파 알고리즘 상세, 활성화 함수 및 원리 (0) | 2024.02.01 |
| 14일차 - 경사하강, 결정트리, 앙상블 학습, 랜덤 포레스트, 교차검증과 그리드 서치 (1) | 2024.01.30 |
| 13일차 - 로지스틱 회귀, 딥러닝을 위한 기초수학, 선형 회귀, 경사하강, 다중 선형 회귀 (2) | 2024.01.29 |
| 12일차 - k-최근접 이웃 회귀, 선형회귀, 다항 회귀, 다중 분류, 특성공학, 규제 선형 모델 (0) | 2024.01.26 |



